Barron's SAT Subject Test Math Level 2, 10th Edition (2012)

Part 2. REVIEW OF MAJOR TOPICS

Chapter 3. Numbers and Operations

3.4 Sequences and Series

RECURSIVE SEQUENCES

A sequence is a function with a domain consisting of the natural numbers. A series is the sum of the terms of a sequence.

EXAMPLES

1. Give an example of
(A) an infinite sequence of numbers,
(B) a finite sequence of numbers,
(C) an infinite series of numbers.

SOLUTIONS

(A) is an infinite sequence of numbers with

(B) 2, 4, 6, . . . , 20 is a finite sequence of numbers with t₁ = 2, t₂ = 4, t₃ = 6, . . . , t₁₀ = 20.

(C) is an infinite series of numbers.

2. If , find the first five terms of the sequence.

When 1, 2, 3, 4, and 5 are substituted for n , , and .

The first five terms are .

3. If a₁ = 2 and , find the first five terms of the sequence.

Since every term is expressed with respect to the immediately preceding term, this is called a recursion formula, and the resulting sequence is called a recursive sequence.

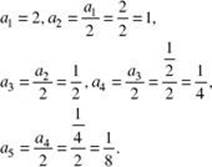
Therefore, the first five terms are . Each term is half of its predecessor.

4. If a₁ = 3 and a_n = 2a_{n – 1} + 5, find a₄.

Put (or a₁) into your graphing calculator, and press ENTER. Then multiply by 2 and add 5. Hit ENTER 3 more times to get a₄ = 59.

5. If a₁ = 1, a₂ = 1, and a_n = a_{n – 1} + a_{n – 2}for , find the first 7 terms of the sequence.

The recursive formula indicates that each term is the sum of the two terms before it. Therefore, the first seven terms of this sequence are 1, 1, 2, 3, 5, 8, 13. This is called the Fibonacci sequence.

A series can be abbreviated by using the Greek letter sigma, , to represent the summation of several terms.

6. (A) Express the series 2 + 4 + 6 + · · · + 20 in sigma notation.

(B) Evaluate

SOLUTIONS

(A) The series 2 + 4 + 6 + + 20 = 2i = 100

(B) = 0² + 1² + 2² + 3² + 4² + 5² = 0 + 1 + 4 + 9 + 16 + 25 = 55.

ARITHMETIC SEQUENCES

One of the most common sequences studied at this level is an arithmetic sequence (or arithmetic progression). Each term differs from the preceding term by a common difference. The first n terms of an arithmetic sequence can be denoted by

t₁, t₁ + d, t₁ + 2d, t₁ + 3d, . . . , t₁ + (n – 1)d

where d is the common difference and t_n = t₁ + (n – 1)d. The sum of n terms of the series constructed from an arithmetic sequence is given by the formula

or

If there is one term falling between two given terms of an arithmetic sequence, it is called their arithmetic mean.

EXAMPLES

1. (A) Find the 28th term of the arithmetic sequence 2, 5, 8, . . . .

(B) Express the sum of 28 terms of the series of this sequence using sigma notation.

(C) Find the sum of the first 28 terms of the series.

SOLUTIONS

(A) t_n = t₁ + (n–1)d
t₁ = 2, d = 3, n = 28
t₂₈ = 2 + 27·3 = 83

(B) or

(C)

s₂₈ = (2 + 83) = 14 85 = 1190

2. If t₈ = 4 and t₁₂ = –2, find the first three terms of the arithmetic sequence.

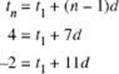
To solve these two equations for d, subtract the second equation from the third.

Substituting in the first equation gives . Thus,

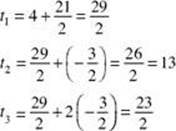
The first three terms are

3. In an arithmetic series, if S_n = 3n² + 2n, find the first three terms.

When n = 1, S₁ = t₁. Therefore, t₁ = 3(1)² + 2 · 1 = 5.

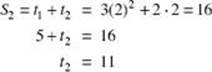
Therefore, d = 6, which leads to a third term of 17. Thus, the first three terms are 5, 11, 17.

GEOMETRIC SEQUENCES

Another common type of sequence studied at this level is a geometric sequence (or geometric progression). In a geometric sequence the ratio of any two successive terms is a constant r called the constant ratio. The first n terms of a geometric sequence can be denoted by

t₁, t₁r, t₁r², t₁r³, . . . , t₁r^n–1 = t_n

The sum of the first n terms of a geometric series is given by the formula

If there is one term falling between two given terms of a geometric sequence it is called their geometric mean.

EXAMPLES

1. (A) Find the seventh term of the geometric sequence 1, 2, 4, . . . , and
(B) the sum of the first seven terms.

(A)

(B)

2. The first term of a geometric sequence is 64, and the common ratio is .

For what value of n is ?

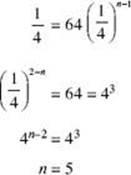
SERIES

In a geometric sequence, if |r| < 1, the sum of the series approaches a limit as n approaches infinity. In the formula the term Therefore, as long as , or

EXAMPLES

1. Evaluate (A) and

(B)

Both problems ask the same question: Find the sum of an infinite geometric series.

(A) When the first few terms, , are listed, it can be seen that and the common ratio . Therefore,

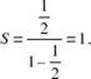
(B) When the first few terms, , are listed, it can be seen that t₁ = 1 and the common ratio . Therefore,

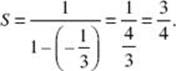
2. Find the exact value of the repeating decimal 0.4545 . . . .

This can be represented by a geometric series, 0.45 + 0.0045 + 0.000045 + · · · , with t₁ = 0.45 and r = 0.01.

Since ,

3. Given the sequence 2, x , y , 9. If the first three terms form an arithmetic sequence and the last three terms form a geometric sequence, find x and y .

From the arithmetic sequence, , substitute to eliminate d.

From the geometric sequence , substitute to eliminate r.

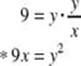
Use the two equations with the * to eliminate y :

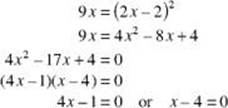
Thus, or 4.

Substitute in y = 2x – 2:

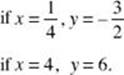
EXERCISES

1. If a₁ = 3 and a_n = n + a_n–1, the sum of the first five terms is

 (A) 17

 (B) 30

 (C) 42

 (D) 45

 (E) 68

2. If a₁ = 5 and find a₃.

 (A) 2.623

 (B) 2.635

 (C) 2.673

 (D) 2.799

 (E) 3.323

3. If the repeating decimal is written as a fraction in lowest terms, the sum of the numerator and denominator is

 (A) 16

 (B) 47

 (C) 245

 (D) 334

 (E) 1237

4. The first three terms of a geometric sequence are The fourth term is

 (A)

 (B)

 (C)

 (D)

 (E)

5. By how much does the arithmetic mean between 1 and 25 exceed the positive geometric mean between 1 and 25?

 (A) 5

 (B) about 7.1

 (C) 8

 (D) 12.9

 (E) 18

6. In a geometric series and . What is r ?

 (A)

 (B)

 (C)

 (D)

 (E)

Answers and Explanations

1. (D) a₂ = 5, a₃ = 8, a₄ = 12, a₅ = 17. Therefore, S₅ = 45

2. * (D) Press 5 ENTER into your graphing calculator. Then enter and press ENTER twice more to get a₃.

3. * (C) The decimal = 0.2 + (0.037 + 0.00037 + 0.0000037 + · · ·), which is 0.2 + an infinite geometric series with a common ratio of 0.01.

  The sum of the numerator and the denominator is 245.

4. (D) Terms are 3^1/4, 3^1/8, 1. Common ratio = 3^–1/8. Therefore, the fourth term is 1 · 3^–1/8 = 3^–1/8 or

5. (C) Arithmetic mean Geometric mean The difference is 8.

6 (D) 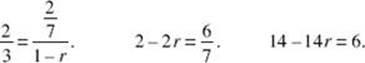Therefore,