Barron's SAT Subject Test Math Level 2, 10th Edition (2012)
Part 2. REVIEW OF MAJOR TOPICS
Chapter 1. Functions
1.3 Trigonometric Functions and Their Inverses
DEFINITIONS
The general definitions of the six trigonometric functions are obtained from an angle placed in standard position on a rectangular coordinate system. When an angle ![]() is placed so that its vertex is at the origin, its initial side is along the positive x-axis, and its terminal side is anywhere on the coordinate system, it is said to be in standard position. The angle is given a positive value if it is measured in a counterclockwise direction from the initial side to the terminal side, and a negative value if it is measured in a clockwise direction.
is placed so that its vertex is at the origin, its initial side is along the positive x-axis, and its terminal side is anywhere on the coordinate system, it is said to be in standard position. The angle is given a positive value if it is measured in a counterclockwise direction from the initial side to the terminal side, and a negative value if it is measured in a clockwise direction.
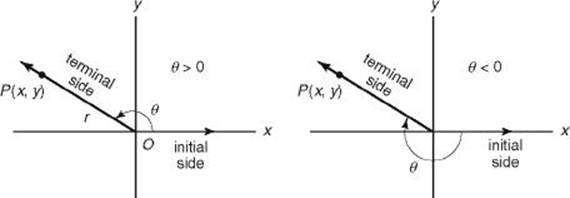
Let P(x,y) be any point on the terminal side of the angle, and let r represent the distance between O and P. The six trigonometric functions are defined to be:
![]()
|
TIP sin θ and cos θ are always between –1 and 1. |
From these definitions it follows that:
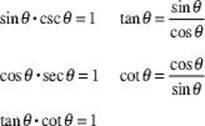
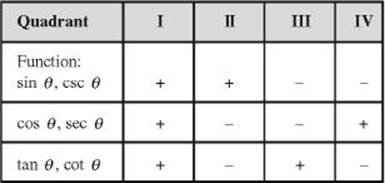
The distance OP is always positive, and the x and y coordinates of P are positive or negative depending on which quadrant the terminal side of ![]() lies in. The signs of the trigonometric functions are indicated in the following table.
lies in. The signs of the trigonometric functions are indicated in the following table.
|
TIP All trig functions are positive in quadrant I. Sine and only sine is positive in quadrant II. Tangent and only tangent is positive in quadrant III. Cosine and only cosine is positive in quadrant IV. Just remember: |
Each angle ![]() whose terminal side lies in quadrant II, III, or IV has associated with it an angle called its reference angle
whose terminal side lies in quadrant II, III, or IV has associated with it an angle called its reference angle ![]() , which is formed by the x-axis and the terminal side.
, which is formed by the x-axis and the terminal side.
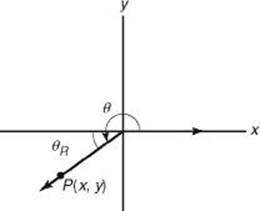
Any trig function of ![]() = ± the same function of
= ± the same function of ![]() . The sign is determined by the quadrant in which the terminal side lies.
. The sign is determined by the quadrant in which the terminal side lies.
EXAMPLES
1. Express sin 320° in terms of ![]() .
.
![]()
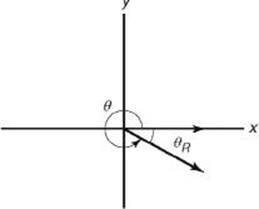
Since the sine is negative in quadrant IV, sin 320° = –sin 40°.
2. Express cot 200° in terms of ![]() .
.
![]()
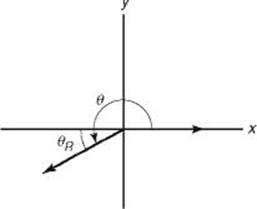
Since the cotangent is positive in quadrant III, cot 200° = cot 20°.
3. Express cos 130° in terms of ![]() .
.
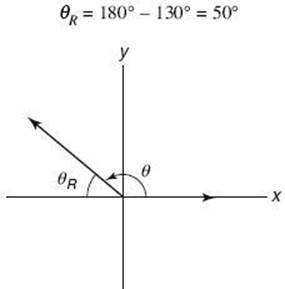
Since the cosine is negative in quadrant II, cos 130° = –cos 50°.
Sine and cosine, tangent and cotangent, and secant and cosecant are cofunction pairs. Cofunctions of complementary angles are equal. If ![]() and
and ![]() are complementary, then trig (
are complementary, then trig (![]() ) = cotrig (
) = cotrig (![]() ) and trig (
) and trig (![]() ) = cotrig (
) = cotrig (![]() ) .
) .
4. If both the angles are acute and sin (3x + 20°) = cos (2x – 40°), find x.
Since these cofunctions are equal, the angles must be complementary.
Therefore, ![]()
EXERCISES
1. Express cos 320° as a function of an angle between 0° and 90°.
(A) cos 40°
(B) sin 40°
(C) cos 50°
(D) sin 50°
(E) none of the above
2. If point P(–5,12) lies on the terminal side of ![]() in standard position, sin
in standard position, sin ![]() =
=
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
3. If ![]() and sin
and sin ![]() , then tan
, then tan ![]() =
=
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) none of the above
4. If x is an angle in quadrant III and tan (x – 30°) = cot x, find x.
(A) 240°
(B) 225°
(C) 210°
(D) 60°
(E) none of the above
5. If 90° < ![]() < 180° and 270° <
< 180° and 270° < ![]() < 360°, then which of the following cannot be true?
< 360°, then which of the following cannot be true?
(A) sin ![]() = sin
= sin ![]()
(B) tan ![]() = sin
= sin ![]()
(C) tan ![]() = tan
= tan ![]()
(D) sin ![]() = cos
= cos ![]()
(E) sec ![]() = csc
= csc ![]()
6. Expressed as a function of an acute angle, cos 310° + cos 190° =
(A) –cos 40°
(B) cos 70°
(C) –cos 50°
(D) sin 20°
(E) –cos 70°
ARCS AND ANGLES
Although the degree is the chief unit used to measure an angle in elementary mathematics courses, the radian has several advantages in more advanced mathematics. A radian is one radius length. The circle shown in the figure below has radius r. The circumference of this circle is 360°, or 2π radians, so one radian is ![]() .
.
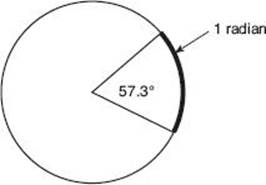
EXAMPLES
1. In each of the following, convert the degrees to radians or the radians to degrees. (If no unit of measurement is indicated, radians are assumed.)
(A) 30°
(B) 270°
(C) ![]()
(D) ![]()
(E) 24
|
TIP Although R is used to indicate radians, a radian actually has no units, so the use of R is optional. |
SOLUTIONS
(A) To change degrees to radians multiply by ![]() , so 30° = 30°
, so 30° = 30° ![]() .
.
(B) 270° ![]()
(C) To change radians to degrees, multiply by ![]() , so
, so ![]()
(D) ![]()
(E) ![]()
In a circle of radius r inches with an arc subtended by a central angle of ![]() measured in radians, two important formulas can be derived. The length of the arc, s, is equal to r
measured in radians, two important formulas can be derived. The length of the arc, s, is equal to r![]() , and the area of the sector, AOB, is equal to
, and the area of the sector, AOB, is equal to ![]() .
.
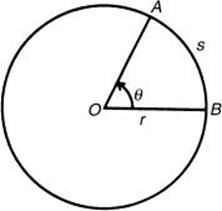
2. Find the area of the sector and the length of the arc subtended by a central angle of ![]() radians in a circle whose radius is 6 inches.
radians in a circle whose radius is 6 inches.
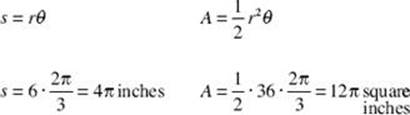
3. In a circle of radius 8 inches, find the area of the sector whose arc length is 6π inches.
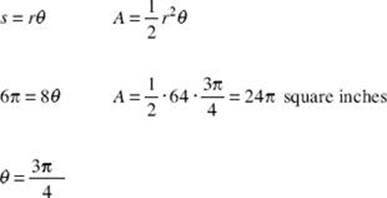
4. Find the length of the radius of a circle in which a central angle of 60° subtends an arc of length 8π inches.
The 60° angle must be converted to radians:
60° = 60° ![]() radians =
radians = ![]() radians
radians
Therefore,
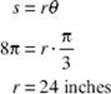
EXERCISES
1. An angle of 30 radians is equal to how many degrees?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
2. If a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
(A) 1
(B) 2
(C) 3
(D) 6
(E) 12
3. If a circle has a circumference of 16 inches, the area of a sector with a central angle of 4.7 radians is
(A) 10
(B) 12
(C) 15
(D) 25
(E) 48
4. A central angle of 40° in a circle of radius 1 inch intercepts an arc whose length is s. Find s.
(A) 0.7
(B) 1.4
(C) 2.0
(D) 3.0
(E) 40
5. The pendulum on a clock swings through an angle of 25°, and the tip sweeps out an arc of 12 inches. How long is the pendulum?
(A) 1.67 inches
(B) 13.8 inches
(C) 27.5 inches
(D) 43.2 inches
(E) 86.4 inches
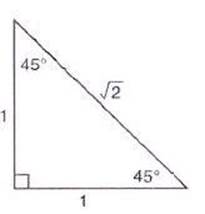
SPECIAL ANGLES
When you use a calculator to evaluate most trig values, you will get a decimal approximation. You can use your knowledge of the definitions of the trigonometric functions, reference angles, and the ratios of the sides of the 45°-45°-90° triangle and the 30°-60°-90° triangle (“special” triangles) to get exact trig values for “special” angles: multiples of 30° ![]() , 45°
, 45° ![]() , 60°
, 60° ![]() .
.
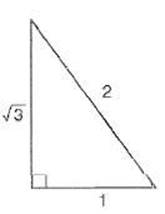
The ratios of the sides of the two special triangles are shown in the figure below.
45° -45° -90° Triangle
30°- 60° -90° Triangle
To illustrate how this can be done, suppose you want to find the trig values of 120° ![]() First sketch the following graph.
First sketch the following graph.
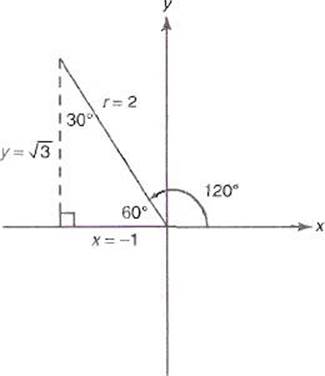
The graph shows the angle in standard position, the reference angle 60°, and the (signed) side length ratios for the 30°-60°-90° triangle. You can now use the definitions of the trig functions to find the trig values:
|
|
|
|
|
|
|
|
|
Values can be checked by comparing the decimal approximation the calculator provides for the trig function with the decimal approximation obtained by entering the exact value in a calculator. In this example, sin 120° ![]() 0.866 and
0.866 and ![]() .
.
You can also readily obtain trig values of the quadrantal angles—multiples of 90° ![]() . The terminal sides of these angles are the x- and y-axes. In these cases, you don’t have a triangle at all; instead, either x or y equals 1 or –1, the other coordinate equals zero, and r equals 1. To illustrate how to use this method to evaluate the trig values of 270°, first draw the figure below.
. The terminal sides of these angles are the x- and y-axes. In these cases, you don’t have a triangle at all; instead, either x or y equals 1 or –1, the other coordinate equals zero, and r equals 1. To illustrate how to use this method to evaluate the trig values of 270°, first draw the figure below.
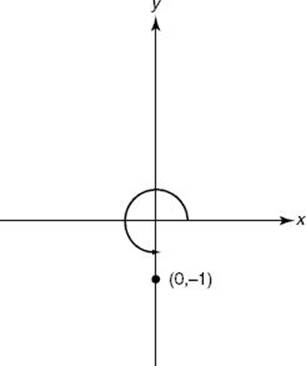
The figure indicates x = 0 and y = –1 (r = 1). Therefore,
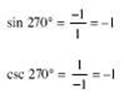
![]()
![]() which is undefined
which is undefined
![]() , which is undefined
, which is undefined
![]()
EXERCISES
1. The exact value of tan (–60°) is
(A) –![]()
(B) –1
(C) ![]()
(D) ![]()
(E) ![]()
2. The exact value of cos ![]()
(A) –1
(B) ![]()
(C) ![]()
(D) ![]()
(E) 0
3. Csc 540° is
(A) 0
(B) –![]()
(C) ![]()
(D) –1
(E) undefined
GRAPHS
Analyzing the graph of a trigonometric function can be readily accomplished with the aid of a graphing calculator. Such an analysis can determine the amplitude, maximum, minimum, period, or phase shift of a trig function, or solve a trig equation or inequality.
The examples and exercises in this and the next two sections show how a variety of trig problems can be solved without using a graphing calculator. They also explain how to solve trig equations and inequalities and how to analyze inverse trig functions.
Since the values of all the trigonometric functions repeat themselves at regular intervals, and, for some number p, f(x) = f(x + p) for all numbers x, these functions are called periodic functions. The smallest positive value of p for which this property holds is called the period of the function.
The sine, cosine, secant, and cosecant have periods of 2![]() , and the tangent and cotangent have periods of
, and the tangent and cotangent have periods of ![]() . The graphs of the six trigonometric functions, shown below, demonstrate that the tangent and cotangent repeat on intervals of length
. The graphs of the six trigonometric functions, shown below, demonstrate that the tangent and cotangent repeat on intervals of length ![]() and that the others repeat on intervals of length 2
and that the others repeat on intervals of length 2![]() .
.
The domain and range of each of the six trigonometric functions are summarized in the table.
PARENT TRIG FUNCTION

Trig functions can be transformed just like any other function. They can be translated (slid) horizontally or vertically or dilated (stretched or shrunk) horizontally or vertically. The general form of a trigonometric function is y = A · trig(Bx + C) + D, where trig stands for sin, cos, tan, csc, sec, or cot. The parameters A and D accomplish vertical translation and dilation, while B and C accomplish horizontal translation and dilation. When working with trig functions, the vertical dilation results in the amplitude, whose value is |A|. If B is factored out of Bx + C we get ![]() . The horizontal translation is
. The horizontal translation is ![]() and is called the phase shift, and the horizontal dilation of trig functions is measured as the period, which is the period of the parent trig function divided by B. Finally, D is the amount of vertical translation.
and is called the phase shift, and the horizontal dilation of trig functions is measured as the period, which is the period of the parent trig function divided by B. Finally, D is the amount of vertical translation.
|
TIP The frequency of a trig function is the reciprocal of its period. Graphs of the parent trig functions follow. |
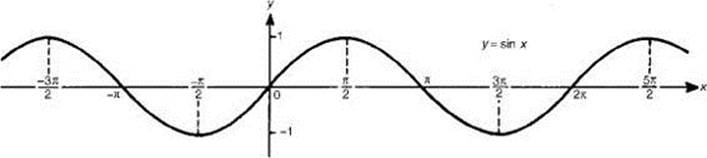
|
TIP sin x is an odd function. |
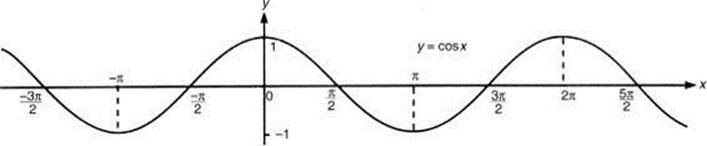
|
TIP Note: cos x is an even function. |
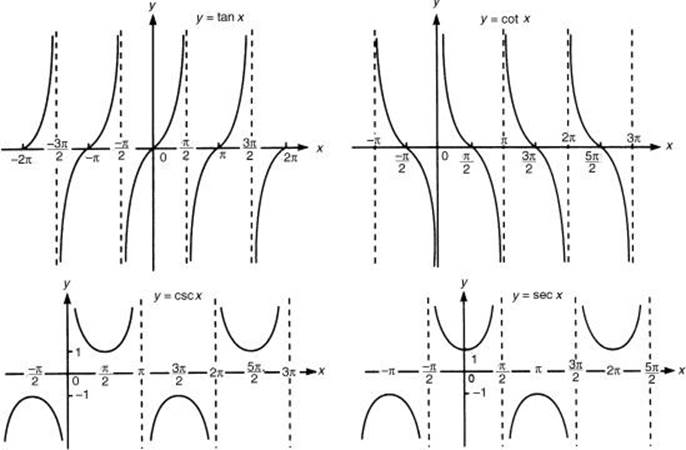
EXAMPLES
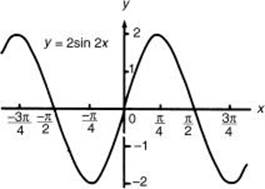
1. Determine the amplitude, period, and phase shift of y = 2sin 2x and sketch at least one period of the graph.
A = 2, B = 2, C = 0, D = 0
![]()
Since the phase shift is zero, the sine graph starts at its normal position, (0,0), and is drawn out to the right and to the left.
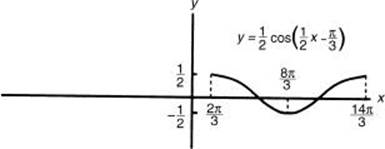
2. Determine the amplitude, period, and phase shift of ![]() and sketch at least one period of the graph.
and sketch at least one period of the graph.
Although a graphing calculator can be used to determine the amplitude, period, and phase shift of a periodic function, it may be more efficient to derive them directly from the equation.
![]()

Since the phase shift is ![]() , the cosine graph starts at x =
, the cosine graph starts at x = ![]() instead of x = 0 and one period ends at
instead of x = 0 and one period ends at ![]()
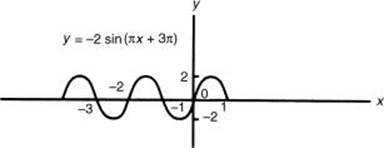
3. Determine the amplitude, period, and phase shift of y = –2 sin(![]() x + 3
x + 3![]() ) and sketch at least one period of the graph.
) and sketch at least one period of the graph.
A = –2, B = π, C = 3π, D = 0
Amplitude = 2
Period = ![]()
Phase shift = ![]()
Since the phase shift is –3, the sine graph starts at x = –3 instead of x = 0, and one period ends at –3 + 2 or x = –1. The graph can continue to the right and to the left for as many periods as desired. Since the coefficient of the sine is negative, the graph starts down as x increases from –3, instead of up as a normal sine graph does.
EXERCISES
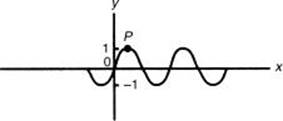
1. In the figure, part of the graph of y = sin 2x is shown. What are the coordinates of point P?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
2. The figure below could be a portion of the graph whose equation is
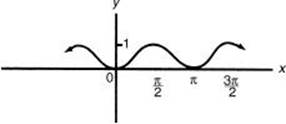
(A) y – 1 = sin x · cos x
(B) y sec x = 1
(C) 2y + 1 = sin 2x
(D) 2y + 1 = cos 2x
(E) 1 – 2y = cos 2x
3. As ![]() increases from
increases from ![]() , the value of
, the value of ![]()
(A) increases, and then decreases
(B) decreases, and then increases
(C) decreases throughout
(D) increases throughout
(E) decreases, increases, and then decreases again
4. The function ![]() cos x + sin x has an amplitude of
cos x + sin x has an amplitude of
(A) 1.37
(B) 1.73
(C) 2
(D) 2.73
(E) 3.46
5. For what value of P is the period of the function ![]() Px equal to
Px equal to ![]() ?
?
(A) ![]()
(B) ![]()
(C) 2
(D) 3
(E) 6
6. If ![]() , what is the maximum value of the function
, what is the maximum value of the function ![]() ?
?
(A) 0
(B) ![]()
(C) ![]()
(D) ![]()
(E) 1
7. If the graph in the figure below has an equation of the form y = sin (Mx + N), what is the value of N?
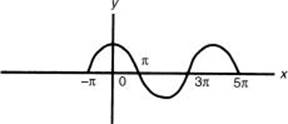
(A) –![]()
(B) –1
(C) –![]()
(D) ![]()
(E) ![]()
IDENTITIES, EQUATIONS, AND INEQUALITIES
There are a few trigonometric identities you must know for the Mathematics Level 2 Subject Test.
• Reciprocal Identities recognize the definitional relationships:
![]()
• Cofunction Identities were discussed earlier. Using radian measure:
![]()
![]()
![]()
• Pythagorean Identities ![]()
• Double Angle Formulas 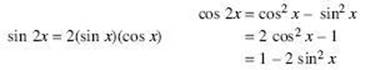
EXAMPLES
1. Given cos ![]() and
and ![]() , find
, find ![]()
Since sin 2![]() = 2(sin
= 2(sin ![]() )(cos
)(cos ![]() ), you need to determine the value of sin
), you need to determine the value of sin ![]() . From the figure below, you can see that sin
. From the figure below, you can see that sin ![]() . Therefore, sin
. Therefore, sin ![]() .
.
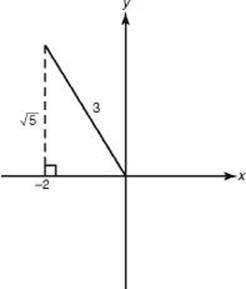
2. If cos 23° = z, find the value of cos 46° in terms of z.
Since 46 = 2(23), a double angle formula can be used: cos 2A = 2 cos2 A – 1. Substituting 23° for A, cos 46° = cos 2(23°) = 2 cos2 23° – 1 = 2(cos 23°)2 – 1 = 2z 2 – 1.
3. If sin x = A, find cos 2x in terms of A.
Using the identity cos 2x = 1 – sin2 x, you get cos 2x = 1 – A2.
You may be expected to solve trigonometric equations on the Math Level 2 Subject Test by using your graphing calculator and getting answers that are decimal approximations. To solve any equation, enter each side of the equation into a function (Yn), graph both functions, and find the point(s) of intersection on the indicated domain by choosing an appropriate window.
4. Solve 2 sin x + cos 2x = 2 sin2 x – 1 for 0 ![]() x
x ![]() 2
2![]() .
.
Enter 2 sin x + cos 2x into Y1 and 2 sin2 x – 1 into Y2. Set Xmin = 0, Xmax = 2![]() , Ymin = –4, and Ymax = 4. Solutions (x-coordinates of intersection points) are 1.57, 3.67, and 5.76.
, Ymin = –4, and Ymax = 4. Solutions (x-coordinates of intersection points) are 1.57, 3.67, and 5.76.
5. Find values of x on the interval [0,![]() ] for which cos x < sin 2x.
] for which cos x < sin 2x.
Enter each side of the inequality into a function, graph both, and find the values of x where the graph of cos x lies beneath the graph of sin 2x: 0.52 < x < 1.57 or x > 2.62.
EXERCISES
1. If sin ![]() and cos
and cos ![]() , find the value of sin 2x.
, find the value of sin 2x.
(A) –![]()
(B) –![]()
(C) ![]()
(D) ![]()
(E) ![]()
2. If tan A = cot B, then
(A) A = B
(B) A = 90° + B
(C) B = 90° + A
(D) A + B = 90°
(E) A + B = 180°
3. If cos ![]() , find cos 2x.
, find cos 2x.
(A) –0.87
(B) –0.25
(C) 0
(D) 0.5
(E) 0.75
4. If sin 37° = z, express sin 74° in terms of z.
(A) ![]()
(B) 2z 2 + 1
(C) 2z
(D) 2z 2 – 1
(E) ![]()
5. If sin x = –0.6427, what is csc x?
(A) –1.64
(B) –1.56
(C) 0.64
(D) 1.56
(E) 1.70
6. For what value(s) of x, 0 < x < ![]() , is sin x < cos x?
, is sin x < cos x?
(A) x < 0.79
(B) x < 0.52
(C) 0.52 < x < 0.79
(D) x > 0.52
(E) x > 0.79
7. What is the range of the function f(x) = 5 – 6sin (![]() x + 1)?
x + 1)?
(A) [–6,6]
(B) [–5,5]
(C) [–1,1]
(D) [–1,11]
(E) [–11,1]
INVERSE TRIG FUNCTIONS
If the graph of any trig function f(x) is reflected about the line y = x, the graph of the inverse (relation) of that trig function is the result. Since all trig functions are periodic, graphs of their inverses are not graphs of functions. The domain of a trig function needs to be limited to one period so that range values are achieved exactly once. The inverse of the restricted sine function is sin–1; the inverse of the restricted cosine function is cos–1, and so forth.

The inverse trig functions are used to represent angles with known trig values. If you know that the tangent of an angle is ![]() , but you do not know the degree measure or radian measure of the angle, tan –1
, but you do not know the degree measure or radian measure of the angle, tan –1 ![]() is an expression that represents the angle between
is an expression that represents the angle between ![]() whose tangent is
whose tangent is ![]() .
.
You can use your graphing calculator to find the degree or radian measure of an inverse trig value.
EXAMPLES
1. Evaluate the radian measure of tan–1 ![]() .
.
Enter 2nd tan ![]() with your calculator in radian mode to get 0.73 radian.
with your calculator in radian mode to get 0.73 radian.
2. Evaluate the degree measure of sin–1 0.8759.
Enter 2nd sin (.8759) with your calculator in degree mode to get 61.15°.
3. Evaluate the degree measure of sec–1 3.4735.
First define x = sec–1 3.4735. If sec x = 3.4735, then cos ![]() . Therefore, enter 2nd cos
. Therefore, enter 2nd cos ![]() with your calculator in degree mode to get 73.27°.
with your calculator in degree mode to get 73.27°.
If “trig” is any trigonometric function, trig(trig–1 x) = x. However, because of the range restriction on inverse trig functions, trig–1(trig x) need not equal x.
4. Evaluate cos (cos–1 0.72).
cos(cos–1 0.72) = 0.72.
5. Evaluate sin–1 (sin 265°).
Enter 2nd sin–1(sin(265)) with your calculator in degree mode to get –85°. This is because –85° is in the required range [–90°,90°], and –85° has the same reference angle as 265°.
6. Evaluate sin ![]() .
.
Let ![]() . Then cos
. Then cos ![]() and x is in the first quadrant. See the figure below.
and x is in the first quadrant. See the figure below.
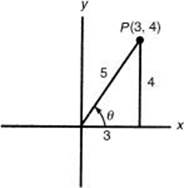
Use the Pythagorean identity sin2x + cos2 x = 1 and the fact that x is in the first quadrant to get sin ![]() .
.
EXERCISES
1. Find the number of degrees in ![]() .
.
(A) –45
(B) –22.5
(C) 0
(D) 22.5
(E) 45
2. Find the number of radians in cos–1(–0.5624).
(A) –0.97
(B) 0.97
(C) 1.77
(D) 2.16
(E) none of these
3. Evaluate tan–1(tan 128°).
(A) –128°
(B) –52°
(C) 52°
(D) 128°
(E) none of these
4. Find the number of radians in cot–1(–5.2418).
(A) –10.80
(B) –5.30
(C) –1.38
(D) –0.19
(E) none of these
5. Which of the following is (are) true?
I. sin–11 + sin–1(–1) = 0
II. cos–11 + cos–1(–1) = 0
III. cos–1 x = cos–1(–x) for all x in the domain of cos–1
(A) only I
(B) only II
(C) only III
(D) only I and II
(E) only II and III
6. Which of the following is a solution of cos3x = ![]() ?
?
(A) 60°
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
TRIANGLES
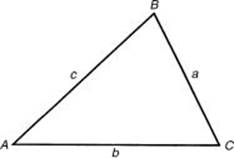
The final topic in trigonometry concerns the relationship between the angles and sides of a triangle that is not a right triangle. Depending on which of the sides and angles of the triangle are supplied, the following formulas can be used to find missing parts of a triangle. In ![]() ABC
ABC
Law of Sines: ![]()
used when the lengths of two sides and the value of the angle opposite one, or two angles and the length of one side are given.
Law of Cosines: 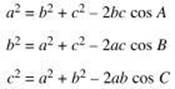
used when the lengths of two sides and the included angle, or the lengths of three sides, are given.
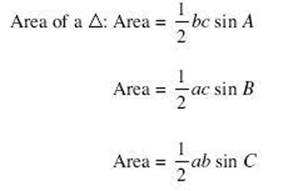
used when two sides and the included angle are given.
EXAMPLES
1. Find the number of degrees in the largest angle of a triangle whose sides are 3, 5, and 7.
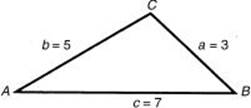
The largest angle is opposite the longest side. Use the Law of Cosines:
![]()
Therefore, cos ![]() .
.
Since cos C < 0 and ![]() C is an angle of a triangle, 90° <
C is an angle of a triangle, 90° < ![]() C < 180°.
C < 180°.
Therefore, ![]() C = 120°.
C = 120°.
2. Find the number of degrees in the other two angles of ![]() ABC if
ABC if ![]() , b = 150, and
, b = 150, and ![]() C = 30°.
C = 30°.
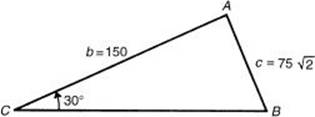
Use the law of sines:
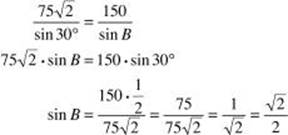
Therefore, ![]() B = 45° or 135°;
B = 45° or 135°; ![]() A = 105° or 15° since there are 180° in the sum of the three angles of a triangle.
A = 105° or 15° since there are 180° in the sum of the three angles of a triangle.
3. Find the area of ![]() ABC if a = 180 inches, b = 150 inches, and
ABC if a = 180 inches, b = 150 inches, and ![]() C = 30°.
C = 30°.
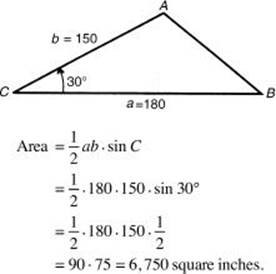
Ambiguous Cases
If the lengths of two sides of a triangle and the angle opposite one of those sides are given, it is possible that two triangles, one triangle, or no triangle can be constructed with the data. This is called the ambiguous case. If the lengths of sides a and b and the value of ![]() A are given, the length of side b determines the number of triangles that can be constructed.
A are given, the length of side b determines the number of triangles that can be constructed.
Case 1: If ![]() A > 90° and a
A > 90° and a ![]() b, no triangle can be formed because side a would not reach the base line. If a > b, one obtuse triangle can be drawn.
b, no triangle can be formed because side a would not reach the base line. If a > b, one obtuse triangle can be drawn.
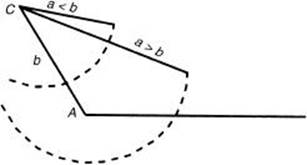
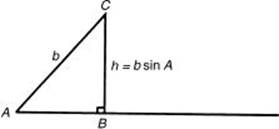
Let the length of the altitude from C to the base line be h. From the basic definition of sine, sin ![]() and thus, h = b sin A.
and thus, h = b sin A.
Case 2: If ![]() A < 90° and side a < b sin A, no triangle can be formed. If a = b sin A, one triangle can be formed. If a > b, there also will be only one triangle. If, on the other hand, b sin A < a < b, two triangles can be formed.
A < 90° and side a < b sin A, no triangle can be formed. If a = b sin A, one triangle can be formed. If a > b, there also will be only one triangle. If, on the other hand, b sin A < a < b, two triangles can be formed.
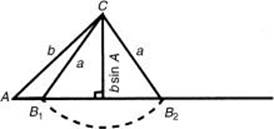
If a compass is opened the length of side a and a circle is drawn with center at C, the circle will cut the baseline at two points, B1 and B2. Thus, ![]() AB1C satisfies the conditions of the problem, as does
AB1C satisfies the conditions of the problem, as does ![]() AB2C.
AB2C.
EXAMPLES
1. How many triangles can be formed if a = 24, b = 31, and ![]() A = 30°?
A = 30°?
Because ![]() A < 90°, b · sin A = 31 · sin 30° = 31 ·
A < 90°, b · sin A = 31 · sin 30° = 31 ·![]() = 15
= 15![]() · Since b · sin A < a < b, there are two triangles.
· Since b · sin A < a < b, there are two triangles.
2. How many triangles can be formed if a = 24, b = 32, and ![]() A = 150°?
A = 150°?
Since ![]() A > 90° and a < b, no triangle can be formed.
A > 90° and a < b, no triangle can be formed.
EXERCISES
1. In ![]() ABC,
ABC, ![]() A = 30°, b = 8, and a =4
A = 30°, b = 8, and a =4![]() . Angle C could equal
. Angle C could equal
(A) 45°
(B) 135°
(C) 60°
(D) 15°
(E) 90°
2. In ![]() ABC,
ABC, ![]() A = 30°, a = 6, and c = 8. Which of the following must be true?
A = 30°, a = 6, and c = 8. Which of the following must be true?
(A) 0° < ![]() C < 90°
C < 90°
(B) 90° < ![]() C < 180°
C < 180°
(C) 45° < ![]() C < 135°
C < 135°
(D) 0° < ![]() C < 45° or 90° <
C < 45° or 90° < ![]() C < 135°
C < 135°
(E) 0° < ![]() C < 45° or 135° <
C < 45° or 135° < ![]() C < 180°
C < 180°
3. The angles of a triangle are in a ratio of 8 : 3 : 1. The ratio of the longest side of the triangle to the next longest side is
(A) ![]()
(B) 8 : 3
(C) ![]()
(D) 8 : 5
(E) ![]()
4. The sides of a triangle are in a ratio of 4 : 5 : 6. The smallest angle is
(A) 82°
(B) 69°
(C) 56°
(D) 41°
(E) 27°
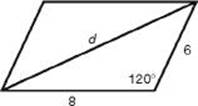
5. Find the length of the longer diagonal of a parallelogram if the sides are 6 inches and 8 inches and the smaller angle is 60°.
(A) 8
(B) 11
(C) 12
(D) 7
(E) 17
6. What are all values of side a in the figure below such that two triangles can be constructed?
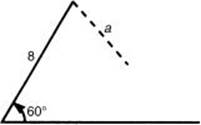
(A) ![]()
(B) a > 8
(C) ![]()
(D) ![]()
(E) ![]()
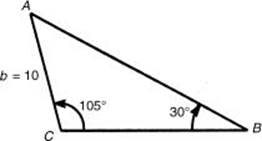
7. In ![]() ABC,
ABC, ![]() B = 30°,
B = 30°, ![]() C = 105°, and b = 10. The length of side a equals
C = 105°, and b = 10. The length of side a equals
(A) 7
(B) 9
(C) 10
(D) 14
(E) 17
8. The area of ![]() ABC, = 24
ABC, = 24![]() , side a = 6, and side b = 16. The value of
, side a = 6, and side b = 16. The value of ![]() C is
C is
(A) 30°
(B) 30° or 150°
(C) 60°
(D) 60° or 120°
(E) none of the above
9. The area of ![]() ABC= 12
ABC= 12![]() , side a = 6, and side b = 8. Side c =
, side a = 6, and side b = 8. Side c =
(A) 2![]()
(B) 2![]()
(C) 2![]() or 2
or 2![]()
(D) 10
(E) 10 or 12
10. Given the following data, which can form two triangles?
I. ![]() C = 30°, c = 8, b = 12
C = 30°, c = 8, b = 12
II. ![]() B = 45°, a = 12
B = 45°, a = 12![]() , b = 15
, b = 15![]()
III. ![]() C = 60°, b = 12, c =5
C = 60°, b = 12, c =5![]()
(A) only I
(B) only II
(C) only III
(D) only I and II
(E) only I and III
Answers and Explanations
Definitions
1. (A) Reference angle is 40°. Cosine in quadrant IV is positive.
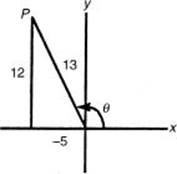
2. (D) See corresponding figure. Therefore, sin ![]() .
.
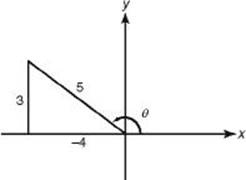
3. (D) Angle ![]() is in quadrant II since sec < 0 and sin > 0. Therefore, tan
is in quadrant II since sec < 0 and sin > 0. Therefore, tan ![]() .
.
4. (A) Cofunctions of complementary angles are equal. x – 30 + x = 90 finds a reference angle of 60° for x. The angle in quadrant III that has a reference angle of 60° is 240°.
5. (A) Angle ![]() is in quadrant II, and sin
is in quadrant II, and sin ![]() is positive. Angle
is positive. Angle ![]() is in quadrant IV, and sin
is in quadrant IV, and sin ![]() is negative.
is negative.
* 6. (E) Put your calculator in degree mode, cos 310° + cos 190° ![]() 0.643 + (–0.985)
0.643 + (–0.985) ![]() – 0.342. Checking the answer choices shows that –cos 70°
– 0.342. Checking the answer choices shows that –cos 70° ![]() –0.342.
–0.342.
Arcs and Angles
1. (E) ![]() .
.
2. (D) ![]()
![]()
* 3. (C) 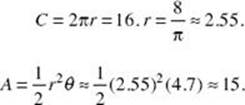
* 4. (A) ![]() ≈ 0.7
≈ 0.7
s = r![]() ≈ 1(0.7) ≈ 0.7.
≈ 1(0.7) ≈ 0.7.
* 5. (C) Change 25° to 0.436 radian ![]() .
.
s = r![]() , and so 12 = r(0.436) and r = 27.5 inches.
, and so 12 = r(0.436) and r = 27.5 inches.
Special Angles
1. (A) Sketch a –60° angle in standard position as shown in the figure below.
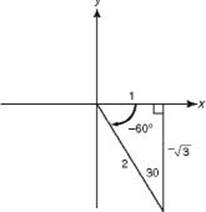
The tangent ratio is ![]()
2. (C) Sketch an angle of ![]() radians in standard position, as shown in the figure below.
radians in standard position, as shown in the figure below.
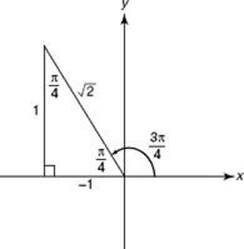
The cosine ratio is ![]() .
.
3. (E) First, determine an angle between 0° and 360° that is coterminal with 540° by subtracting 360° from 540° repeatedly until the result is in this interval. In this case, one subtraction suffices. Since coterminal angles have the same trig values, csc 540° = csc 180°. Sketch the figure below
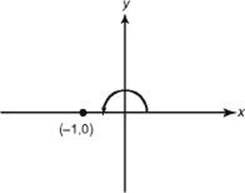
In a quadrantal angle r = 1, and the cosecant ratio is ![]() , which is undefined.
, which is undefined.
Graphs
1. (C) Period ![]() . Point P is
. Point P is ![]() of the way through the period. Amplitude is 1 because the coefficient of sin is 1. Therefore, point P is at
of the way through the period. Amplitude is 1 because the coefficient of sin is 1. Therefore, point P is at ![]() .
.
2. (E) Amplitude = ![]() . Period =
. Period = ![]() . Graph translated
. Graph translated ![]() unit up. Graph looks like a cosine graph reflected about x-axis and shifted up
unit up. Graph looks like a cosine graph reflected about x-axis and shifted up ![]() unit.
unit.
* 3. (C) Graph 4cos ![]() using ZOOM/ZTRIG and observe that the portion of the graph between
using ZOOM/ZTRIG and observe that the portion of the graph between ![]() is decreasing.
is decreasing.
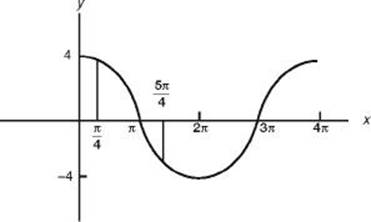
* 4. (C) Graph the function and determine its maximum (2) and minimum (–2). Subtract and then divide by 2.
5. (D) Period = ![]() .
.
* 6. (C) Graph the function using 0 for Xmin and ![]() for Xmax. Observe that the maximum occurs when x =
for Xmax. Observe that the maximum occurs when x =![]() . Then
. Then ![]() .
.
7. (D) Period ![]() (from the figure), so M =
(from the figure), so M = ![]() . Phase shift for a sine curve in the figure is –
. Phase shift for a sine curve in the figure is –![]() . Therefore,
. Therefore, ![]() x + N = 0 when x = –
x + N = 0 when x = –![]() . Therefore,
. Therefore, ![]()
Identities, Equations, and Inequalities
* 1. (A) sin 2x = 2 sin x cos ![]() .
.
2. (D) Since tangent and cotangent are cofunctions, tan A = cot(90° – A), so B = 90° – A, and A + B = 90°.
* 3. (D) ![]()
4. (A) sin 74° = 2 sin 37° cos 37°. Since ![]() . Since 74° is in the first quadrant, the positive square root applies, so cos
. Since 74° is in the first quadrant, the positive square root applies, so cos ![]() .
.
* 5. (B) ![]() .
.
* 6. (A) Graph y = sin x and y = cos in radian mode using the Xmin = 0 and Xmax = ![]() . Observe that the first graph is beneath the second on [0,0.79].
. Observe that the first graph is beneath the second on [0,0.79].
7. (D) Remember that the range of the sine function is [–1,1], so the second term ranges from 6 to –6.
Inverse Trig Functions
* 1. (E) Set your calculator to degree mode, and enter 2nd sin–1 ![]() .
.
* 2. (D) Set your calculator to radian mode, and enter 2nd cos–1(–0.5624).
* 3. (B) Set your calculator to degree mode, and enter 2nd tan–1(tan 128°).
* 4. (E) The range of inverse cotangent functions consists of only positive numbers.
5. (A) Since ![]() , I is true. Since cos–11 = 0 and cos–1(–1) =
, I is true. Since cos–11 = 0 and cos–1(–1) = ![]() , II is not true. Since the range of cos–1 is [0,
, II is not true. Since the range of cos–1 is [0,![]() ], III is not true because cos–1 can never be negative.
], III is not true because cos–1 can never be negative.
6. (E) 3x = arccos ![]() , and so x =
, and so x =![]() arccos
arccos![]() .
.
Triangles
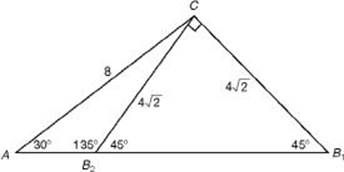
1. (D) Law of Sines: 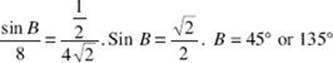 . The figure shows two possible locations for B, labeled B1 and B2, where m
. The figure shows two possible locations for B, labeled B1 and B2, where m ![]() AB1C = 45° and m
AB1C = 45° and m ![]() AB2C = 135°. Corresponding to these, m
AB2C = 135°. Corresponding to these, m ![]() ACB1 = 105° and m
ACB1 = 105° and m ![]() ACB2 = 15°. Of these, only 15° is an answer choice.
ACB2 = 15°. Of these, only 15° is an answer choice.
* 2. (E) By the Law of Sines: ![]() . The figure below shows this to be an ambiguous case (an angle, the side opposite, and another side), so
. The figure below shows this to be an ambiguous case (an angle, the side opposite, and another side), so ![]() or C = 180° – 41.81° = 138.19°.
or C = 180° – 41.81° = 138.19°.
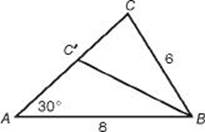
3. (A) The angles are 15°, 45°, and 120°. Let c be the longest side and b the next longest. 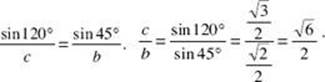
* 4. (D) Use the Law of Cosines. Let the sides be 4, 5, and 6. 16 = 25 + 36 – 60 cos A. Cos ![]() , which implies that
, which implies that ![]()
* 5. (C) Law of Cosines: d2 = 36 + 64 – 96 cos 120°. d2 = 148. Therefore, d ![]() 12.
12.
6. (D) Altitude to base= 8 sin 60° = 4![]() . Therefore, 4
. Therefore, 4![]() < a < 8.
< a < 8.
* 7. (D) A = 45°. Law of Sines: ![]() . Therefore, a = 10
. Therefore, a = 10![]()
![]() 14.
14.
8. (D) Area ![]() . Therefore, C = 60° or 120°.
. Therefore, C = 60° or 120°.
9. (C) Area ![]() . C = 60° or 120°. Use Law of Cosines with 60° and then with 120°.
. C = 60° or 120°. Use Law of Cosines with 60° and then with 120°.
Note: At this point in the solution you know there have to be two values for C. Therefore, the answer must be Choice C or E. If C = 10 (from Choice E), ABC is a right triangle with area = ![]() · 6 · 8 = 24. Therefore, Choice E is not the answer, and so Choice C is the correct answer.
· 6 · 8 = 24. Therefore, Choice E is not the answer, and so Choice C is the correct answer.
10. (A) In I the altitude ![]() and so 2 triangles.
and so 2 triangles. ![]() so only 1 triangle. In III the altitude
so only 1 triangle. In III the altitude ![]() so no triangle.
so no triangle.