Barron's SAT Subject Test Math Level 2, 10th Edition (2012)
Part 2. REVIEW OF MAJOR TOPICS
Chapter 2. Geometry and Measurement
2.1 Coordinate Geometry
TRANSFORMATIONS AND SYMMETRY
The three types of transformations in the coordinate plane are translations, stretches/shrinks, and reflections. Translation preserves the shape of a graph, only moving it around the coordinate plane. Translation is accomplished by addition. Changing the scale (stretching and shrinking) can change the shape of a graph. This is accomplished by multiplication. Finally, reflection preserves the shape and size of a graph but changes its orientation. Reflection is accomplished by negation.
Suppose y = f(x) defines any function.
• y = f(x) + k translates y = f(x) k units vertically (up if k > 0; down if k < 0)
• y = f(x – h) translates y = f(x) h units horizontally (right if h > 0; left if h < 0)
EXAMPLES
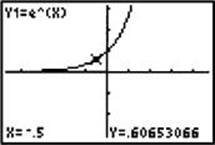
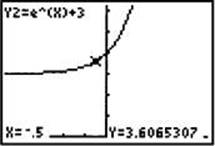
1. Suppose y = f(x) = ex . Describe the graph of y = ex + 3.
In this example, k = 3, so ex + 3 = f(x) + 3. As shown in the figures below, each point on the graph of y = ex + 3 is 3 units above the corresponding point on the graph of y = ex .
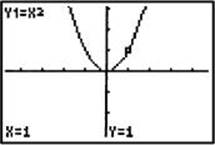
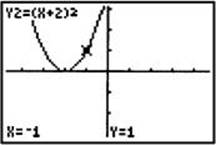
2. Suppose y = x2. Describe the graph of y = (x + 2)2.
In this example h = –2, so (x + 2)2 = f(x + 2). As shown in the figures below, each point on the graph of y = (x + 2)2 is 2 units to the left of the corresponding point on the graph of y = x2.
• y = af(x) stretches (shrinks) f(x) vertically by a factor of |a| if |a| > 1(|a| < 1).
• y = f(ax) shrinks (stretches) f(x) horizontally by a factor of ![]() if |a| > 1(|a| < 1).
if |a| > 1(|a| < 1).
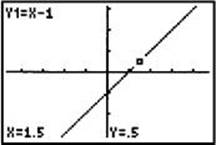
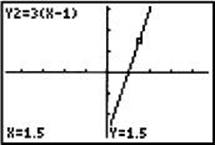
3. Suppose y = x – 1. Describe the graph of y = 3(x – 1).
In this example |a| = 3, so 3(x + 1) = 3f(x). As shown in the graphs below, for x = 1.5 the y-coordinate of each point on the graph of y = 3(x – 1) is 3 times the y-coordinate of the corresponding point on the graph of y = x – 1.
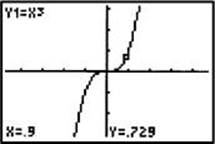
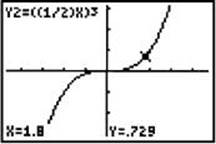
4. Suppose y = x3. Describe the graph of ![]() .
.
In this example, ![]() . As shown in the graphs below, for y = 0.729 the x-coordinate of each point on the graph of
. As shown in the graphs below, for y = 0.729 the x-coordinate of each point on the graph of ![]() is 2 times the x- coordinate of the corresponding point on the graph of y = x3.
is 2 times the x- coordinate of the corresponding point on the graph of y = x3.
• y = –f(x) reflects y = f(x) about the x -axis. (The reflection is vertical.)
• y = f (–x) reflects y = f(x) about the y-axis. (The reflection is horizontal.)
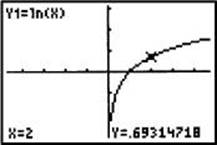
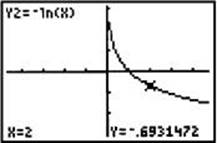
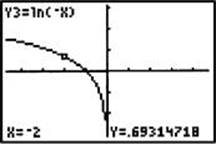
5. Suppose y = ln x . Describe the graphs of y = –ln x and y = ln(–x).
As shown in the graphs below, the graph of y = –ln x is the reflection of the graph of y = ln x about the x -axis, and the graph of y = ln (–x) is the reflection about the y-axis.
Translations, stretching/shrinking, and reflections can be combined to produce functions. Vertical transformations occur when adding, multiplying, or negating takes place after the function is applied (i.e., to y). The order in which multiple vertical transformations are executed does not matter. Horizontal transformations occur when adding, multiplying, or negating takes place before the function is applied (i.e., to x). These transformations must be taken in the following order: reflect; change the scale; then translate. Moreover, the scale factor |a| must be factored out of a translation.
6. Suppose y = f(x). Use words to describe the transformation y = f (–ax + b).
Observe that all of these transformations are horizontal. First we have to write –ax + b as ![]() . The x-coordinate of a point (x,y) on the graph of y = f(x) goes through the following sequence of transformations: reflected about the y-axis; horizontally shrunk by a factor of
. The x-coordinate of a point (x,y) on the graph of y = f(x) goes through the following sequence of transformations: reflected about the y-axis; horizontally shrunk by a factor of ![]() or stretched by a factor of |a|; and translated
or stretched by a factor of |a|; and translated ![]() to the right.
to the right.
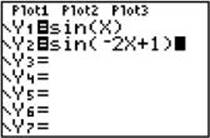
7. Suppose y = sin x . Describe the sequence of transformations to get the graph of y = sin(–2x + 1).
Observe that all transformations are horizontal. Write the function as ![]() . Consider the point (4,–0.7568 . . .) on the graph of y = sin x . First reflect this point about the y-axis to (–4,–0.7568...). Then shrink by a factor of
. Consider the point (4,–0.7568 . . .) on the graph of y = sin x . First reflect this point about the y-axis to (–4,–0.7568...). Then shrink by a factor of ![]() to (–2,–0.7568...). Then translate
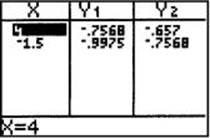
to (–2,–0.7568...). Then translate ![]() units right, to (–1.5,–0.7568...). The screens below show Y1 = sin x and Y2 = sin(–2x + 1) and a table showing the points (4,–0.7568...) for Y1 and (–1.5,–0.7568...) for Y2.
units right, to (–1.5,–0.7568...). The screens below show Y1 = sin x and Y2 = sin(–2x + 1) and a table showing the points (4,–0.7568...) for Y1 and (–1.5,–0.7568...) for Y2.
Reflections about the x - and y-axes represent two types of symmetry in a graph. Symmetry through the origin is a third type of graphical symmetry. A graph defined by an equation in x and y is symmetrical with respect to the
• x -axis if replacing x by –x preserves the equation;
• y-axis if replacing y by –y preserves the equation; and
• origin if replacing x and y by –x and –y, respectively, preserves the equation.
These symmetries are defined for functions as follows:
• Symmetry about the y-axis: f(x) = f (–x) for all x .
• Symmetry about the x -axis: f(x) = –f(x) for all x .
• Symmetry about the origin: f(x) = –f (–x) for all x .
As defined previously, functions that are symmetric about the y-axis are even functions, and those that are symmetric about the origin are odd functions.
8. Discuss the symmetry of f(x) = cos x .
Since cos x = cos (–x), cosine is symmetric about the y-axis (an even function).
However, since cos x ![]() –cos x and cos (–x)
–cos x and cos (–x) ![]() –cos x, the cosine is not symmetric with respect to the x -axis or origin.
–cos x, the cosine is not symmetric with respect to the x -axis or origin.
9. Discuss the symmetry of x2 + xy + y2 = 0.
If you substitute –x for x or –y for y, but not both, the equation becomes x2 – xy + y2 = 0, which does not preserve the equation. Therefore, the graph is not symmetrical with respect to either axis. However, if you substitute both –x for x and –y for y, the equation is preserved, so the equation is symmetric about the origin.
EXERCISES
1. Which of the following functions transforms y = f(x) by moving it 5 units to the right?
(A) y = f(x + 5)
(B) y = f(x – 5)
(C) y = f(x) + 5
(D) y = f(x) – 5
(E) y = 5f(x)
2. Which of the following functions stretches y = cos (x) vertically by a factor of 3?
(A) y = cos(x + 3)
(B) y = cos(3x)
(C) ![]()
(D) y = 3 cos x
(E) ![]()
3. The graph of y = f(x) is shown.
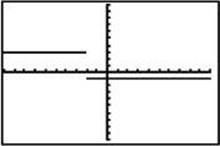
Which of the following is the graph of y = f (–x) – 2?
(A) 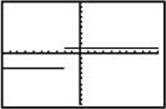
(B) 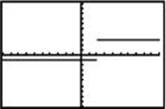
(C) 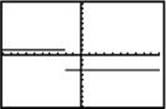
(D) 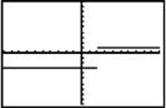
(E) 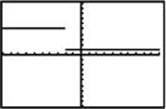
4. Which of the following is a transformation of y = f(x) that translates this function down 3, shrinks it horizontally by a factor of 2, and reflects it about the x -axis.
(A) y = –2f(x – 3)
(B) y = f (–2x) – 3
(C) ![]()
(D) y = –f (2x) – 3
(E) ![]()
CONIC SECTIONS
Geometrically, the conic sections are formed by the intersection of a plane and the two nappes of a right cone. The plane does not intersect the cone’s vertex (see below). In a parabola, the plane is parallel to a lateral edge of the cone. In a hyperbola, the plane is parallel to the axis of the cone. In an ellipse the plane is not parallel to either a lateral edge or the axis of the cone. Intersections that contain the cone’s vertex are called degenerate conics and are not covered on the Math Level 2 Test.
parabola

hyperbola
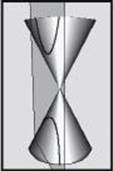
ellipse
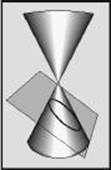
Conics are also defined in terms of points in the coordinate plane. Formulas for the distance between two points and the distance between a point and a line are then used to derive standard equations of the conics. Each conic has a pair of standard equations, depending on whether the conic has an orientation to the x - or y-axis. With one exception described later, these are the only cases covered in the Math Level 2 Test.
Parabolas
A parabola is the set of points that are equidistant from a given point (focus) and a given line (directrix).
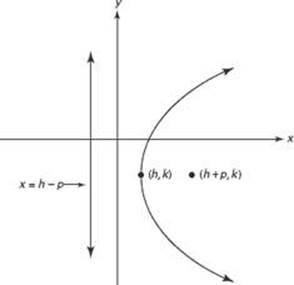
If a parabola has an x- orientation:
• It opens to the left or right.
• The standard equation is (y – k)2 = 4p(x – h).
• The focus is (h + p, k), and the directrix is x = h – p.
• The vertex is (h, k).
• The common distance from the parabola to the focus and directrix is |p |.
• If p > 0, the parabola opens to the right; if p < 0, it opens to the left.
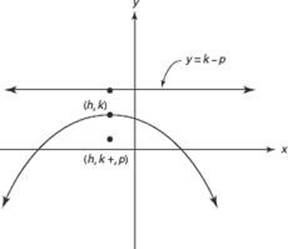
If a parabola has a y-orientation:
• It opens up or down.
• The standard equation is (x – h)2 = 4p(y – k).
• The focus is (h, k + p), and the directrix is y = k – p.
• The vertex is (h, k).
• The common distance from the parabola to the focus and directrix is |p |.
• If p > 0, the parabola opens up; if p < 0, it opens down.
These points are illustrated in the figures below.
Graph of (y – k)2 = 4p(x – h) p > 0
Graph of (x – h)2 = 4p(y – k) p < 0
TIP ![]()
When you studied quadratics in Algebra 2, x was the squared variable and the parabolas opened up or down. This should help you determine the correct orientation when you look at the equation.
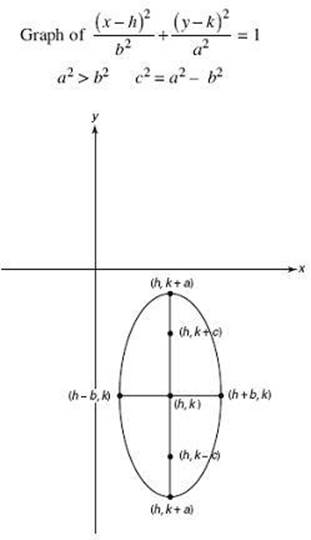
Ellipses
An ellipse is the set of points whose distances from two given points (foci, plural of focus) sum to a constant.
If an ellipse has an x -orientation:
• The standard equation is ![]() , where a2 > b2.
, where a2 > b2.
• The major axis is parallel to the x -axis.
• The center is (h, k).
• The vertices are (h – a, k) and (h + a, k), the endpoints of the major axis. So the major axis is 2a units long.
• The endpoints of the minor axis are (h, k – b) and (h, k + b). So the minor axis is 2b units long.
• The foci are on the major axis. Each focus is at a distance of ![]() from the center, so the foci are at (h – c, k) and (h + c, k).
from the center, so the foci are at (h – c, k) and (h + c, k).
If an ellipse has a y -orientation:
• The standard equation is ![]() , where a2 > b2.
, where a2 > b2.
• The major axis is parallel to the y-axis.
• The center is (h, k).
• The vertices are (h, k – a) and (h, k + a), the endpoints of the major axis.
• The endpoints of the minor axis are (h – b, k) and (h + b, k).
• The foci are on the major axis. Each focus is at a distance of ![]() from the center, so the foci are at (h, k – c) and (h, k + c).
from the center, so the foci are at (h, k – c) and (h, k + c).
If the larger denominator in an equation of an ellipse is under the x-term, the ellipse has an x-orientation. If the larger denominator is under the y-term, the ellipse has a y-orientation.
Note that an ellipse with a = b is a circle whose equation is (x – h)2 + (y – k)2 = r2, where r is the common value of a and b .
These points are illustrated in the figures below.
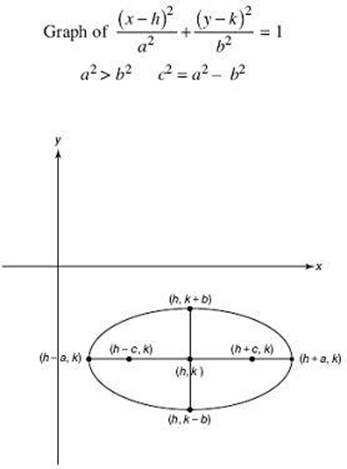
Hyperbolas
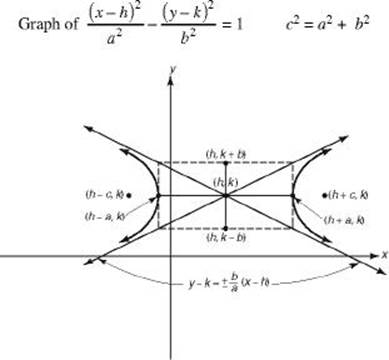
A hyperbola is the set of points whose distances from two fixed points (foci) differ by a constant. A hyperbola has two halves, corresponding to the two nappes of the cone. Each half has a vertex and sides that are asymptotic to a pair of intersecting lines.
If a hyperbola has an x-orientation:
• The hyperbola opens to the sides.
• The standard equation is ![]() .
.
• The center is (h, k).
• The vertices are (h – a, k) and (h + a, k). The segment joining the two vertices is called the transverse axis. This axis is horizontal and has length 2a .
• The foci are on the transverse axis. The distance between the center and each focus is ![]() , so the foci are (h – c, k) and (h + c, k).
, so the foci are (h – c, k) and (h + c, k).
• The vertical segment through the center with endpoints (h, k – b) and (h, k + b), which has length 2b, is called the conjugate axis. The endpoints of this axis are not on the hyperbola.
• The equations of the asymptotes are ![]() .
.
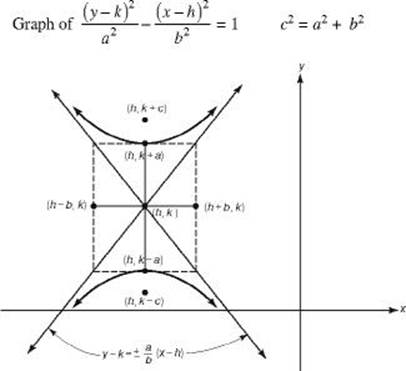
If a hyperbola has a y-orientation:
• The hyperbola opens up and down.
• The standard equation is ![]() .
.
• The center is (h, k).
• The vertices are (h, k – a) and (h, k + a). The transverse axis is vertical and has length 2a .
• The foci are (h, k – c) and (h, k + c).
• The conjugate axis is horizontal, has endpoints (h – b, k) and (h + b, k), and has length 2b .
• The equations of the asymptotes are ![]()
If the x-term of the equation is positive, the hyperbola has an x-orientation. If the y-term is positive, it has a y-orientation.
These points are illustrated in the figures below.
The statement made earlier, that the only conic sections considered in the Math Level 2 test are those with axes parallel to the x - or y-axis, has one exception. The equation xy = k, where k is a constant, is the equation of a rectangular hyperbola where the asymptotes are the x - and y -axes. If k > 0, the branches of the hyperbola lie in the first and third quadrants. Otherwise, the branches lie in the second and fourth quadrants.
Eccentricity
The eccentricity of an ellipse or hyperbola is a measure of its degree of elongation. The eccentricity of an ellipse is ![]() , which is less than 1 since c < a . The closer c is to a, the more circular the ellipse. The eccentricity of a hyperbola is also
, which is less than 1 since c < a . The closer c is to a, the more circular the ellipse. The eccentricity of a hyperbola is also ![]() . However, it is greater than 1 since c > a in a hyperbola. The farther c is from a, the more elongated the hyperbola.
. However, it is greater than 1 since c > a in a hyperbola. The farther c is from a, the more elongated the hyperbola.
EXAMPLES
1. ![]()
Which conic section does this equation define? Also find, if they exist,
(i) the center
(ii) the vertex/vertices
(iii) the focus/foci
(iv) the directrix
(v) the asymptotes
(vi) the eccentricity
This is a hyperbola with a y -orientation. In this problem, h = 1, k = 3, a = 3, b = 4, and ![]() .
.
(i) The center is (1, 3).
(ii) The vertices are (1, 0) and (1, 6).
(iii) The foci are (1, –2) and (1, 8).
(iv) A hyperbola does not have a directrix.
(v) The asymptotes are ![]() .
.
(vi) The eccentricity is ![]() .
.
2. (y + 4)2 = –6(x – 2)
Which conic section does this equation define? Also find, if they exist,
(i) the center
(ii) the vertex/vertices
(iii) the focus/foci
(iv) the directrix
(v) the asymptotes
(vi) the eccentricity
This is a parabola with an x -orientation opening left. In this problem, h = 2, k = –4, and ![]() .
.
(i) A parabola does not have a center.
(ii) The vertex is (2, –4).
(iii) The focus is ![]() .
.
(iv) The directrix is ![]() .
.
(v) A parabola does not have asymptotes.
(vi) A parabola does not have eccentricity.
3. ![]()
Which conic section does this equation define? Also find, if they exist,
(i) the center
(ii) the vertex/vertices
(iii) the focus/foci
(iv) the directrix
(v) the asymptotes
(vi) the eccentricity
This is an ellipse with a y-orientation since the larger denominator has y in the numerator. In this problem h = –3, k = 8, a = 10, b = 5, and ![]() .
.
(i) The center is (–3, 8).
(ii) The vertices are (–3, –2) and (–3, 18).
(iii) The foci are ![]() and
and ![]() .
.
(iv) An ellipse does not have a directrix.
(v) An ellipse does not have asymptotes.
(vi) The eccentricity is ![]() .
.
If an equation of a conic is not in standard form, completing the square will yield a standard-form equation. If the equation has squared terms in both x and y, completing the square in both variables will result in the standard equation of an ellipse or hyperbola. If only one of the variables is squared in the original equation, completing the square in that variable will result in the standard equation of a parabola.
4. Name the conic by finding its standard-form equation.
2x2 + 3y2 + 12x – 24y + 60 = 0
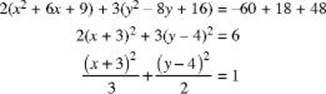
This conic is an ellipse.
5. Name the conic by finding its standard-form equation.
4x2 + 4y2 – 12x – 20y – 2 = 0
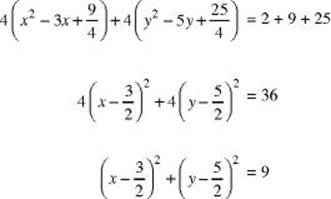
This is a circle with center ![]() and radius 3.
and radius 3.
6. Find the foci of the conic y2 + 2x + 2y = 5.
Since there is only one squared term, the conic is a parabola. A parabola has only one focus, (h + p, k) . Complete the square in y to get the standard equation:
(y + 1)2 = −2(x − 3)
Therefore, h = 3, k = −1, and p = ![]() .
.
The focus is ![]() .
.
7. Find the standard equation of a hyperbola with center (3, –4), vertices (3, 1) and (3, 7), and asymptotes ![]() .
.
Since the vertices have the same x-coordinate, the hyperbola has a y-orientation. The length of the transverse axis is 6, implying that a = 3. The slope of the asymptote is ![]() , so b = 4. The center is (h, k), so h = 3 and k = –4.
, so b = 4. The center is (h, k), so h = 3 and k = –4.
The standard equation is ![]() .
.
EXERCISES
1. Which of the following is a focus of ![]()
(A) (1, –1)
(B) (2, –1)
(C) (3, –1)
(D) (2, –2)
(E) (–2, 1)
2. Which of the following is an asymptote of 3x2 – 4y2 – 12 = 0?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
3. The standard equation of a parabola with focus (2, –3) and directrix x = 6 is
(A) x – 2 = 8(y + 3)2
(B) x – 4 = –8(y + 3)2
(C) y + 3 = 8(x – 2)2
(D) y – 3 = –8(x + 2)2
(E) y – 3 = –8(x + 4)2
4. The standard equation of an ellipse with vertices (–5, 2) and (3, 2) and minor axis of length 6 is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
5. Which of the following is a vertex of 16x2 – y2 – 32x – 6y – 57 = 0?
(A) (1, –1)
(B) (1, 3)
(C) (1, 5)
(D) (–1, –3)
(E) (–1, 3)
6. The graph of x2 = (2y + 3)2 is
(A) an ellipse
(B) a parabola
(C) a hyperbola
(D) a circle
(E) none of these
POLAR COORDINATES
Although the most common way to represent a point in a plane is in terms of its distances from two perpendicular axes, there are several other ways. One such way is in terms of the distance of the point from the origin and the angle between the positive x -axis and the ray emanating from the origin going through the point.
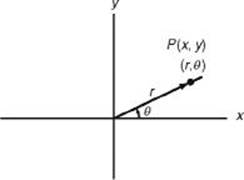
In the figure, the regular rectangular coordinates of P are (x,y) and the polar coordinates are ![]() . If r > 0, it is measured along the ray of the terminal side of
. If r > 0, it is measured along the ray of the terminal side of ![]() . If r < 0, it is measured in the direction of the opposite ray.
. If r < 0, it is measured in the direction of the opposite ray.
Since ![]() and
and ![]() , there is an easy relationship between rectangular and polar coordinates:
, there is an easy relationship between rectangular and polar coordinates:
![]()
![]()
x2 + y2 = r2, using the Pythagorean theorem.
Unlike the case involving rectangular coordinates, each point in the plane can be named by an infinite number of polar coordinates.
EXAMPLES
1. (2,30°), (2,390°), (2,–330°), (–2,210°), (–2,–150°) all name the same point.
In general, a point in the plane represented by ![]() can also be represented by
can also be represented by ![]() or
or ![]() , where n is an integer.
, where n is an integer.
2. Express point P, whose rectangular coordinates are ![]() , in terms of polar coordinates.
, in terms of polar coordinates.
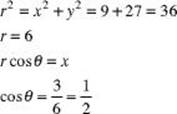
Therefore, ![]() = 60°and (6,60°) are the polar coordinates of P .
= 60°and (6,60°) are the polar coordinates of P .
3. Describe the graphs of (A) r = 2 and (B)![]() .
.
(A) r2 = x2 + y2
r = 2
Therefore, x2 + y2 = 4, which is the equation of a circle whose center is at the origin and whose radius is 2.
(B) Since ![]() and
and ![]() , y = 1. The domain of
, y = 1. The domain of ![]() is all real
is all real ![]() that are not multiples of
that are not multiples of ![]() .
.
Thus, ![]() is the equation of a horizontal line with holes in it at multiples of
is the equation of a horizontal line with holes in it at multiples of ![]() one unit above the x -axis.
one unit above the x -axis.
Both r = 2 and ![]() are examples of polar functions. Such functions can be graphed on a graphing calculator by using POLAR mode. Enter 2 into r1 and graph using ZOOM 6, the standard window.
are examples of polar functions. Such functions can be graphed on a graphing calculator by using POLAR mode. Enter 2 into r1 and graph using ZOOM 6, the standard window.
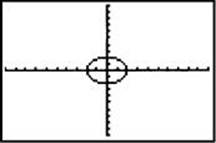
Although the graph is accurate for the scale given, the shape looks like that of an ellipse, not a circle. This is because the standard screen has a scale on the x -axis that is larger than that on the y-axis, resulting in a distorted graph. The graph below is obtained by using the ZOOM ZSquare command.
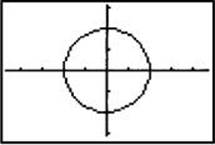
EXERCISES
1. A point has polar coordinate (2,60°). The same point can be represented by
(A) (–2,240°)
(B) (2,240°)
(C) (–2,60°)
(D) (2,–60°)
(E) (2,–240°)
2. The polar coordinates of a point P are (2,200°). The rectangular coordinates of P are
(A) (–1.88,–0.68)
(B) (–0.68,–1.88)
(C) (–0.34,–0.94)
(D) (–0.94,–0.34)
(E) (–0.47,–0.17)
3. Describe the graph of ![]() .
.
(A) a parabola
(B) an ellipse
(C) a circle
(D) a vertical line
(E) the x -axis
Answers and Explanations
Transformations and Symmetry
1. (B) Horizontal translation (right) is accomplished by subtracting the amount of the translation (5) from x before the function is applied.
2. (D) Vertical stretching is accomplished by multiplying the function by the stretching factor after the function is applied.
3. (D) The graph of y = f (–x) – 2 reflects y = f (x) about the y-axis and translates it down 2.
4. (D) The horizontal shrinking by a factor of 2 is the multiplication of x by 2 before the function is applied. The reflection about the x -axis is the negation of the function after it is applied. The translation down 3 is the addition of –3 after the function is applied.
Conic Sections
1. (D) This is the standard equation of an ellipse with center (2, –1), a2 = 5, b2 = 4, and y -orientation. Since c2 = a2 – b2 = 1, the foci are 1 unit above and below the center.
2. (C) Complete the square in both x and y to put the equation in standard form:
![]()
This hyperbola has x-orientation, with a2 = 4 and b2 = 3. Its asymptotes are ![]() .
.
3. (B) The directrix is a vertical line 4 units to the right of the focus. Therefore, the parabola has an x-orientation (the y-term is square). The vertex of (4, –3) is 2 units right of the focus, so p = –2.
4. (A) Since the vertices have the same y-coordinate, the major axis is horizontal, has length 8, and a2 = 16. Therefore, the center of the ellipse is (–1, 2). Since the minor axis has length 6, b2 = 9.
5. (D) Complete the square in both x and y to get the standard equation:
![]()
The transverse axis has length 4, so the vertices of the hyperbola are 2 units left and right of the center (1, –3).
6. (C) Expand the right side of the equation and bring all but the constant term to the left side. Complete the square in both x and y to get ![]() , the standard equation of a hyperbola.
, the standard equation of a hyperbola.
Polar Coordinates
1. (A) The angle must either be coterminal with (60 ± 360n) with r = 2 or (60 ± 180)° with r = –2. A is the only answer choice that meets these criteria.
2. * (A) With your calculator in degree mode, evaluate x = r cos ![]() = 2 cos 200
= 2 cos 200 ![]() –1.88 and y = r sin 200 = 2 sin 200
–1.88 and y = r sin 200 = 2 sin 200 ![]() –0.68.
–0.68.
3. * (D) With your graphing calculator in POLAR mode, enter ![]() as r1, and observe that the graph is a vertical line with holes where cos
as r1, and observe that the graph is a vertical line with holes where cos ![]() = 0.
= 0.