Two-Dimensional Calculus (2011)
Chapter 3. Transformations
15. Special linear transformations; composition
Let us consider a linear transformation F of the x, y plane into the x, y plane :

followed by a linear transformation G of the x, y plane into the u, υ plane,

The composition G ![]() F of F and G is a transformation H of the x, y plane into the u, υ plane (Fig. 15.1). The equations of H are found by substituting the expressions for X and Y from Eqs. (15.1) into Eqs. (15.2). Explicitly,
F of F and G is a transformation H of the x, y plane into the u, υ plane (Fig. 15.1). The equations of H are found by substituting the expressions for X and Y from Eqs. (15.1) into Eqs. (15.2). Explicitly,

where
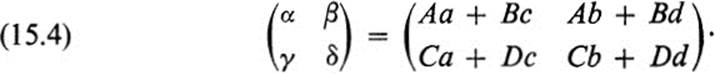
The main conclusions are first, that the composed transformation H is again a linear transformation, and, second, that the determinant of the transformation H is given by
![]()
Equation (15.5) is obtained by direct computation from Eq. (15.4).
This result is sufficiently important to be stated as a separate theorem.
Theorem 15.1 If F and G are any two linear transformations, then their composition G ![]() F is again a linear transformation, and
F is again a linear transformation, and
![]()
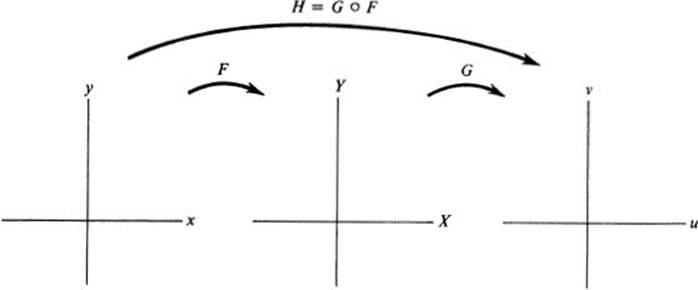
FIGURE 15.1Composition of mappings
It follows that the result of applying any number of successive linear transformations is again a linear transformation.
One way to arrive at an understanding of general linear transformations is to start with some special types of transformations that are easy to visualize, and then build up more complicated ones by a succession of simple ones. We consider now a number of special classes of linear transformations.
Rotations
Let us picture momentarily the x, y plane and the u, υ plane as coinciding, and ask for the equations of the transformation that consists of a rotation of the plane about the origin through an angle α in the positive direction (Fig. 15.2). If, in polar coordinates, we set
![]()
then
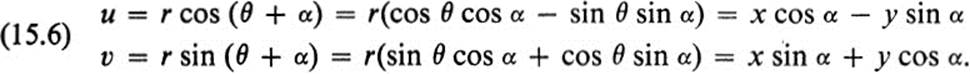
Thus this rotation is a linear transformation, and its matrix is

If we solve Eqs. (15.6) for x and y in terms of u and υ, we find that the equations of the inverse transformation are
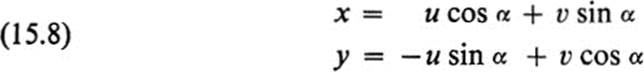
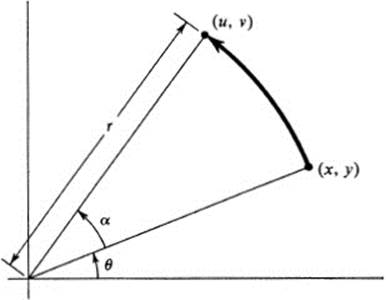
FIGURE 15.2 Rotation through angle α
and therefore that the matrix of the inverse transformation is

Noting that cos (−α) = cos α, sin(−α)= −sin α, we observe that the matrix (15.9) may be derived from (15.7) simply by changing α to − α. With the wisdom of hindsight, we deduce that the inverse transformation (15.8) could have been written down immediately by observing that the inverse of a rotation through an angle a is a rotation through the angle −α.
Reflections
We have already noted in Example 13.7 that the equations u = x, v = −y define a reflection in the horizontal axis. If we wish to find the equations for a reflection in any line through the origin, we may proceed in steps: first, make a rotation so that the line becomes the horizontal axis, then reflect in this axis, and then rotate back again. Specifically, if we want to reflect in a line that makes an angle β with the x axis, we perform the following transformations in succession (Fig. 15.3):

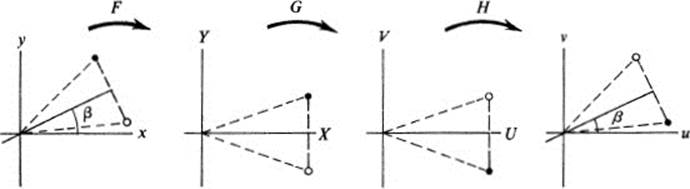
FIGURE 15.3Reflection in line y = x tan β
The resulting transformation is obtained by successively substituting each set of variables into the equations of the following transformation. We find
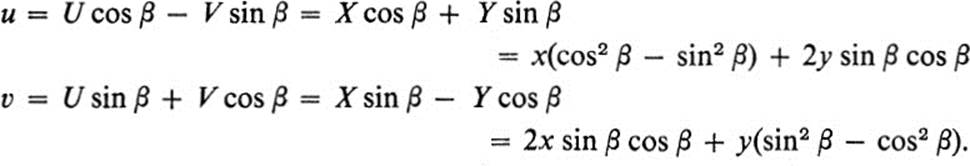
If we set α = 2β, these equations take the form
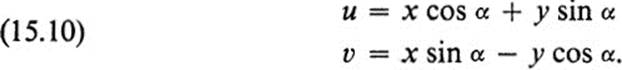
Thus a reflection is a linear transformation with matrix

The resemblance between this matrix and matrices (15.7) and (15.9) corresponding to a rotation is certainly striking. Note, however, the important difference that the determinant of matrix (15.11) is equal to − 1, whereas for both (15.7) and (15.9) the determinant is +1. This is the algebraic confirmation of the geometrically obvious fact that rotations preserve orientation, and reflections reverse orientation.
Dilations
By a dilation we mean a uniform stretching or contraction. Analytically, for some fixed number λ > 0 the image of an arbitrary point (x, y) is the point (u, υ) (Fig. 15.4), where
![]()
Thus the equations of a dilation are

and its matrix is

A basic property of dilations is that not only distances to the origin, but all distances are multiplied by the same constant λ. In other words, if the distance between two points in the x, y plane is d, then the distance between their image points in the u, υ plane will be λd. This follows immediately from Eq. (15.12) and the formula for the distance between two points. In general, the following terminology is used.
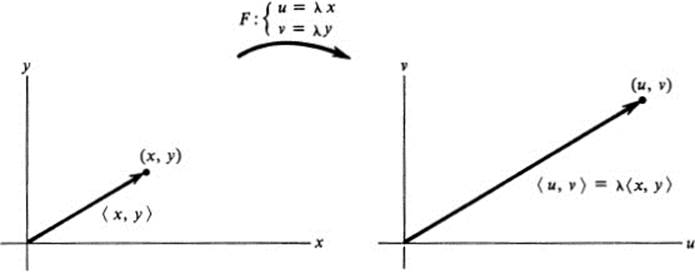
FIGURE 15.4Dilation
Definition 15.1 A similarity transformation is a linear transformation under which all distances are multiplied by a fixed constant λ > 0.
The reason for this terminology is that such a transformation transforms every triangle into a similar triangle.
Now as we have just seen, a dilation is always a similarity transformation. Furthermore, both rotations and reflections are similarity transformations in which λ= 1. That is, both of these types of transformation preserve all distances, as is clear geometrically, and can be verified algebraically by direct substitution in Eqs. (15.6) and (15.10). Finally, since the composition of two similarity transformations is clearly again a similarity transformation, any transformation obtained by composing rotations, reflections, and dilations is a similarity transformation. An important fact is that the converse is also true.
Theorem 15.2 Every similarity transformation consists of a dilation followed by a rotation or reflection.
PROOF.We note first of all that a similarity transformation is always nonsingular. Namely, two distinct points are mapped onto two distinct points, whereas a singular transformation is never one-to-one. Consequently the unit circle x2+ y2 = 1 is mapped onto an ellipse. But since every point on the unit circle is unit distance from the origin, every point on the image must be a distance λ from the origin. Hence the image ellipse is just the circle u2 + υ2 = λ2.
Suppose now that the equations of the transformation are

Then
![]()
and the inverse image of the circle u2+ υ2 = λ2 has the equation
![]()
But this equation must represent the circle x2 + y2 = 1. This means that we must have
![]()
If we introduce the vectors ![]() a, c
a, c![]() ,
, ![]() b, d
b, d![]() these equations reduce to
these equations reduce to
![]()
From the first of these equations we deduce that
![]()
for some number μ, by Lemma 1.1. But since |![]() − c, a
− c, a![]() | =|
| =|![]() a, c
a, c![]() | = (a2 +c2)1/2, we deduce further from the second of Eqs. (15.16) that
| = (a2 +c2)1/2, we deduce further from the second of Eqs. (15.16) that
![]()
and hence |μ| = 1 or μ = ±1. Thus either
![]()
In terms of components, we have
![]()
Finally, again using the second of Eqs. (15.16), we note that ![]() a, c
a, c![]() /λ is a unit vector and hence is of the form
/λ is a unit vector and hence is of the form ![]() cos α, sin α
cos α, sin α![]() for some α. In other words,
for some α. In other words,
![]()
Case 1.If the first alternative in (15.17) holds, then
![]()
Substituting in Eqs. (15.14), the equations of the transformation take the form
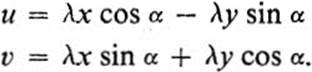
But these equations may be obtained by setting
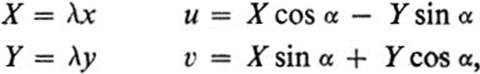
the first of which represents a dilation, and the second a rotation through the angle α (see (15.7)).
Case 2. If the second alternative in (15.17) holds, then by (15.18),
![]()
Substituting in (15.14) yields
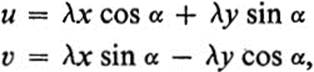
which is the composition of
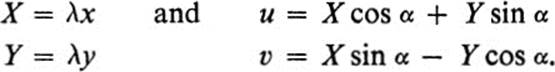
The first of these is again a dilation, but the second is in this case a reflection (see (15.11)).
This concludes the proof of the theorem.![]()
RemarkAn examination of the proof reveals that it falls into two distinct parts. In the first part we showed that if the linear transformation (15.14) is a similarity transformation, then its coefficients must satisfy (15.15). In the second part we deduced that if Eqs. (15.15) hold, then the transformation must consist of a dilation followed by a rotation or a reflection, and hence it must be a similarity transformation. Further, we showed that Eqs. (15.15) imply (15.17), and the converse is obvious. We have therefore the following conclusion.
Corollary The algebraic condition that the general linear transformation (15.14) be a similarity transformation is that any of the equivalent relations (15.15) ,(15.16), or (15.17) on the coefficients should hold.
We are now in a position to characterize two basic classes of linear transformations those which preserve angles and those which preserve distances. We start with the former.
Under a linear transformation every pair of straight lines in the x, y plane maps into a pair of straight lines in the u, υ plane. We say that the transformation preserves angles if the angle between the original pair of lines equals the angle between the image pair of lines. We restrict ourselves to nonsingular transformations, since otherwise certain lines map into a single point, and the angle is not defined.
Theorem 15.3For a nonsingular linear transformation the following are equivalent. The transformation
1.preserves all angles
2.preserves all right angles
3.is a similarity transformation.
PROOF.Clearly, if all angles are preserved then all right angles are preserved. Hence 1 ⇒ 2. To show that 2 ⇒ 3, suppose that every pair of perpendicular lines maps onto a pair of perpendicular lines. Let the transformation be given by
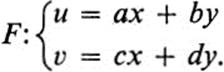
Then F maps the origin into the origin, (1, 0) onto (a, c), and (0, 1) onto (b, d). Thus the image of the x axis is the line through (0, 0) and (a, c), and the image of the y axis is the line through (0, 0) and (b, d). By our assumption the two image lines must be perpendicular. This means that the vectors ![]() a, c
a, c![]() and
and ![]() b, d
b, d![]() are perpendicular:
are perpendicular: ![]() a, c
a, c![]() ⊥
⊥ ![]() b, d
b, d![]() (Fig. 15.5). But this is precisely the first of Eqs. (15.16). Next consider the images of the two diagonal lines y = x and y= − x. Since F maps (1, 1) onto (a+ b, c+ d) and (1, − 1) onto (a − b, c − d), we have
(Fig. 15.5). But this is precisely the first of Eqs. (15.16). Next consider the images of the two diagonal lines y = x and y= − x. Since F maps (1, 1) onto (a+ b, c+ d) and (1, − 1) onto (a − b, c − d), we have ![]() a + b, c + d
a + b, c + d![]() ·
· ![]() a − b, c − d
a − b, c − d![]() = 0, or a2 −
= 0, or a2 − ![]() b2 +c2 − d2 = 0. Thus a2 + c2 = b2 + d2, and setting λ= |
b2 +c2 − d2 = 0. Thus a2 + c2 = b2 + d2, and setting λ= |![]() a, c>
a, c>![]() | = |
| = |![]() b, d
b, d![]() | we see that (15.16) is satisfied. By the Corollary to Th. 15.2, F is a similarity transformation. Finally, the fact that 3 ⇒ 1 is obvious, since a similarity transformation takes every triangle into a similar triangle, and hence all angles are preserved. Thus conditions 1, 2, and 3 are all equivalent, and the theorem is proved.
| we see that (15.16) is satisfied. By the Corollary to Th. 15.2, F is a similarity transformation. Finally, the fact that 3 ⇒ 1 is obvious, since a similarity transformation takes every triangle into a similar triangle, and hence all angles are preserved. Thus conditions 1, 2, and 3 are all equivalent, and the theorem is proved. ![]()
We consider next the class of transformations that preserve all distances.
Theorem 15.4The linear transformations that preserve distances are precisely the rotations and reflections. Algebraically they are characterized by the conditions
![]()
where we assume that the equations of the transformation are in the standard form (15.14).
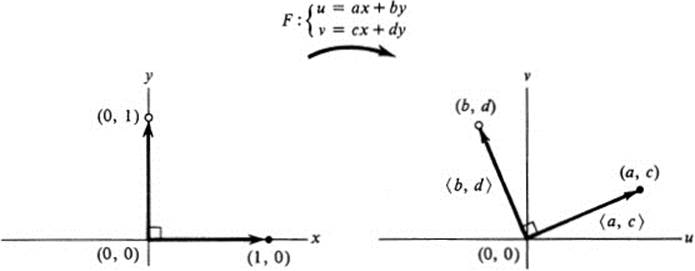
FIGURE 15.5Distance-preserving transformation
PROOF. That a transformation preserves distances means that the images of any pair of points are the same distance apart as the original pair of points. But such a transformation is simply a similarity transformation with λ = 1. The result is then an immediate consequence of Th. 15.2 and its Corollary.![]()
Although this theorem may appear to some as intuitively clear, it has simple consequences that are not so obvious. We give one example.
Corollary The composed transformation obtained by a reflection in some axis followed by a rotation may also be obtained by making a single reflection in a suitable axis.
PROOF. Since both the reflection and rotation preserve distances, so does the composed transformation, which must itself be a reflection or rotation by Th. 15.4. But the determinant of a reflection is − 1, and that of a rotation is + 1. Hence the composed transformation has determinant −1 (Th. 15.1), and it must be a reflection.![]()
The above results on linear transformations are all that we need in our ensuing discussion of differentiable transformations. For the sake of completeness, however, we note the following additional facts.
Consider a transformation of the form

with matrix
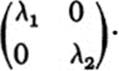
Under such a transformation horizontal distances are multiplied by |λ1| and vertical distances by |λ2|. The over-all effect is easy to visualize. Furthermore, we can then visualize the most general linear transformation by using the following result.
Theorem 15.5Every linear transformation may be obtained by performing in succession first a rotation, then a transformation of the form (15.20), and then another rotation.
The idea of the proof is the following. The unit circle in the x, y plane maps onto an ellipse in the u, υ plane. The lines in the x, y plane which map onto the major and minor axes of the ellipse must be perpendicular, since they correspond to directions in which a quadratic form takes on its maximum and minimum values. Making a rotation in the x, y plane so that these lines go into the coordinate axes, and a rotation in the u, υ plane, which takes the axes of the ellipse into the coordinate axes, the linear transformation reduces to the form (15.20), where the numbers λ1 and λ2 are equal in magnitude to the semimajor and semiminor axes of the ellipse. (See Ex. 15.18 for further details.)
As an application of this result, consider an arbitrary triangle in the x, y plane and its image in the u, υ plane under a given linear transformation. Under a transformation of the form (15.20), the area of this triangle is multiplied by |λ1 λ2| since if we divide the triangle into two parts by a horizontal line through a vertex, each part has the base multiplied by |λ1 | and the altitude by |λ2|. Now let F be an arbitrary linear transformation and denote its determinant by Δ. If we compose F out of rotations and a transformation of the form (15.20), then the determinant of F is the product of the determinants of these transformations. But the determinant of a rotation is equal to 1, and the determinant of the transformation (15.20) is just λ1λ2. Hence Δ = λ1λ2. Finally, since rotations preserve areas, we come to the following conclusion.
CorollaryUnder an arbitrary linear transformation the area of every triangle is multiplied by a fixed constant |Δ|, that is, the absolute value of the determinant of the transformation.
This statement is restricted to triangles, since their area is computed in an elementary fashion. After we have discussed the concept of area for more general figures in the following chapter, it will be clear that the above result holds for such figures (see the Corollary to Th. 26.2).
As a final consequence, we have the result: a linear transformation preserves areas if and only if its determinant Δ satisfies |Δ| = 1, that is Δ = ±1.
Exercises
15.1 Find the matrix of the transformation G ![]() F if the matrices of F and G, respectively, are equal to
F if the matrices of F and G, respectively, are equal to
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
g. ![]()
h. ![]()
15.2Carry out the computation leading from Eq. (15.4) to Eq. (15.5).
15.3Verify Eq. (15.5a) explicitly for each of the pairs F, G in Ex. 15.1.
15.4Prove that the composition of any number of nonsingular linear transformations is again nonsingular.
15.5Prove that the composition of any number of nonsingular linear transformations together with one singular transformation is always singular.
15.6Show that for any two linear transformations F, G
![]()
15.7Find the equations of each of the following linear transformations.
a. A counterclockwise rotation through an angle of ![]() π.
π.
b. A clockwise rotation through an angle of ![]() π
π
c. A reflection in the line x + y = 0.
d. A reflection in the line of positive slope making an angle of ![]() π with the x axis.
π with the x axis.
15.8Show that each of the following transformations is a reflection, and find the line in which the plane is reflected.
a. F1:(x, y)→ (y, x)
b. F2:(x, y)→(x, −y)
c. F3:(x, y)→(−x, y)
15.9Show that the effect of a counterclockwise rotation through 45° followed by a reflection in the line y = x is the same as a single reflection in a certain line, and specify the line.
15.10 a. Using the notation of Ex. 15.8 show that F2 ![]() F1 is a rotation through a certain angle, and determine the angle.
F1 is a rotation through a certain angle, and determine the angle.
b. Do the same for F3 ![]() F2.
F2.
c. Find the equations of the transformation F3 ![]() F2
F2 ![]() F1 and describe this transformation geometrically.
F1 and describe this transformation geometrically.
15.11Show that the result of performing any even number of successive reflections in different lines may also be obtained by a single rotation.
15.12Let F be a similarity transformation that multiplies all distances by λ. Show that the determinant of F is ± λ2.
15.13Show that the inverse of a similarity transformation is also a similarity transformation.
15.14Show that a linear transformation is a similarity transformation if and only if it maps circles onto circles.
15.15Show that the following transformations are similarity transformations by referring to Eqs. (15.17). Then express each as the composition of a dilation and a rotation or reflection.
a. ![]()
b. ![]()
c. ![]()
d. ![]()
15.16Show that if F is a dilation and G is an arbitrary linear transformation, then F ![]() G = G
G = G ![]() F.
F.
15.17Give a geometric description of transformations of the form of (15.20) in each of the following cases.
a. λ1 > 1, λ2 = 1
b.0 < λ1 < 1, λ2 = −1
c. λ1= 0, λ2 = −1
d.−1 < λ1 < 0, λ2 −1
* 15.18Complete the proof of Th. 15.5 in the following steps.
a. Show that if a linear transformation F maps the circle x2 + y2 = 1 onto a circle, then F is already in the form of (15.20), with λ1 = λ2.
b. Verify the statement that if F is nonsingular, and if the circle x2 + y2 = 1 maps onto a certain ellipse, then the inverse images of the axes of that ellipse are perpendicular lines in the x, y plane. (Hint: use Corollary 2 to Th. 10.2.)
c. Show that if a nonsingular linear transformation F maps the x axis into the u axis, the y axis into the υ axis, and the circle x2 + y2 = 1 onto the ellipse ![]() , then F is of the form u = ± λ1x, υ = ±λ2 y. (Hint: observe that the coefficients of a linear transformation F are determined by the action of F on the points (1, 0) and (0, 1).)
, then F is of the form u = ± λ1x, υ = ±λ2 y. (Hint: observe that the coefficients of a linear transformation F are determined by the action of F on the points (1, 0) and (0, 1).)
d. Show that Th. 15.5 holds for a singular transformation, in which case either λ1 or λ2 (or both) will be zero. (Hint: use Ex. 14.5c, and describe the rotations that must be made in the x, y plane and in the u, υ plane.)
15.19Let F be an arbitrary linear transformation :
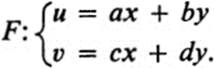
Give a direct proof of the Corollary to Th. 15.5 by carrying out the following steps.
Let (x0, y0), (x1, y1), (x2, y2)be the vertices of an arbitrary triangle T in the x, y plane, and let (uk, υk) = F(xk , yk), k = 0, 1, 2. Let
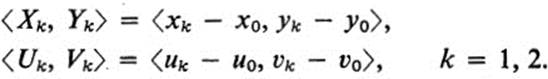
a. Express Uk, υk in terms of Xk, Yk.
b. Express the area A of the triangle T in terms of X1, Y1, X2, Y2 (Hint: see Ex. 1.29d.)
c. Let T ' be the triangle with vertices (u0, υ0), (u1, υ1),(u2, υ2). Express the area of A ' T ' in terms of U1, υ1, U2, υ2.
d. By a direct computation, using parts a, b, c, above, show that A' =| ad − bc|A.
15.20 Let F1, F2 be any two linear transformations, and let Δ1, Δ2 be their determinants. Let Δ be the determinant of F2 ![]() F1.
F1.
a. Using the Corollary to Th. 15.5, give a geometric proof of the fact that
![]()
b. Using the geometric interpretation of the sign of the determinant of a linear transformation, show that if F1 and F2 are both nonsingular, then
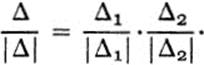
c. Using parts a and b (or part a alone, in case either F1 or F2 is singular) show that we always have
![]()
(Note that this gives both a purely geometric proof and also an important geometric interpretation of Eq. (15.5a).)
*15.21Using the notation of Exs. 14.11 and 14.20-14.24, we associate with an arbitrary linear transformation F, the corresponding linear transformation F of displacement vectors.
a. Show that F is a dilation with constant λ if and only if F(w) = λw for all vectors w.
b. Show that F preserves distances if and only if |F(w)| = |w| for all vectors w.
c. Show that F is a similarity transformation with factor λ if and only if |F(w)| = λ|w| for all vectors w.
d. Show that F preserves distances if and only if F preserves dot products, that is, F(W1)·F(w2) = w1·w2 for all vectors w1, w2. (Hint: if F preserves dot products, set W1 = w2 and use part b. If F preserves distances, use part b and the dentity
![]()
applied to any two vectors w1, w2 and to F(w1) + F(w2) = F(w1 + w2).)
e. Show that F is a similarity transformation with factor λ if and only if F(w1)·F(w2) = λ2w1·w2 for all vectors w1, w2. (Hint: use Th. 15.2 together with parts a and d.)
f. Give a purely analytic proof that if F is a similarity transformation, then F preserves all angles between vectors. (Hint : use parts c and e together with the formula cos α = w1·w2/|w1| |w2|, for the angle α between the vectors w1, w2.)
RemarkGiven matrices

associated with a pair of linear transformations F1, F2, respectively, the product of M1 and M2 is defined to be the matrix associated with the composition of F1 and F2. As is clear, for example by Ex. 15.1e, f, this product depends on the order in which the transformations are performed. Specifically, we define M2M1 to be the matrix of F2 ![]() F1.Then by Eq. (15.4), we have
F1.Then by Eq. (15.4), we have
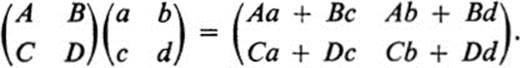
The matrix
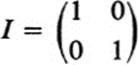
is called the identity matrix and is associated with the identity transformation F, which leaves every point fixed. If M =![]() is associated with a nonsingular transformation F, then
is associated with a nonsingular transformation F, then
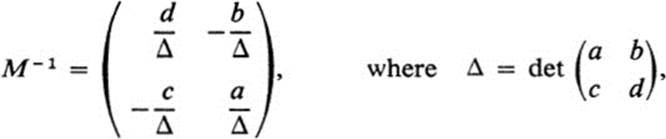
is associated with the inverse transformation F−1 by Eq. (14.7). This matrix M−1 is called the inverse matrix of M. Equation (14.8) takes the form
![]()
where the right-hand side is simply the reciprocal of det M.
We may also define other algebraic operations on matrices in terms of elementary operations on the corresponding linear transformations. Thus
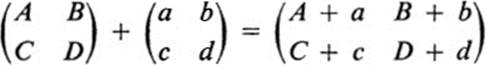
and
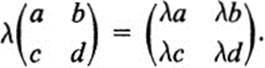
The study of matrices and their properties under these operations is known as matrix algebra. It may be carried out quite independently of any considerations of the associated linear transformations. One advantage of this approach is that matrices have other applications (such as to quadratic forms, in the case of symmetric matrices, as we have seen earlier) and it is not desirable to tie their study to any one interpretation.
The following exercises are designed to illustrate some of the elementary facts of matrix algebra. They are to be carried out by direct application of the matrix operations defined above.
15.22Show that if I is the identity matrix, then
![]()
for every matrix M.
15.23Show that for any matrix M with nonzero determinant,
![]()
15.24Let
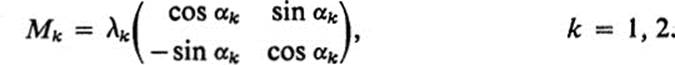
Show that
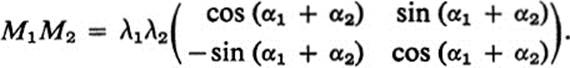
15.25Let M1, M2 be given matrices with det M1 ≠ 0. Show that if λ1,λ2 are the roots of the equation
![]()
then
![]()
15.26Show that the answer to Ex. 10.14, can be written in matrix form as
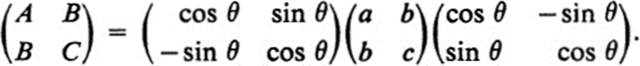
Show how this provides a simple answer to Ex. 10.16.