Two-Dimensional Calculus (2011)

Chapter 3. Transformations

18. Functional dependence; conformal mapping

We start once more with a differentiable transformation,

defined in some domain D. In the previous section we concentrated chiefly on the case where the Jacobian was different from zero at all points in D. We wish now to consider the other extreme, namely those transformations F for which the Jacobian is zero at every point of D. Let us start with the special case in which F is linear,

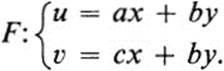
Then

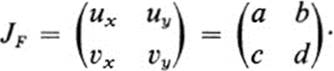
Thus the Jacobian is everywhere equal to zero if and only if the determinant of the linear transformation F is equal to zero. We have seen in Sect. 14 that a linear transformation with zero determinant maps the whole plane into a straight line through the origin. Thus, for linear transformations, the property that the Jacobian is everywhere zero is equivalent to the geometrical property that the whole plane is mapped into some straight line.

Returning to the general transformation (18.1), we ask what it means for F to map the whole domain D into a line through the origin. The equation of such a line is λu + μυ = 0, where λ and μ are constants, and the condition that Fmaps D into that line is that λf(x, y) + μg(x, y) ≡ 0 in D. The following terminology is used.

Definition 18.1 Two functions f(x, y) and g(x, y) defined in a domain D are linearly dependent if there exist numbers λ, μ, not both zero, such that

(See Ex. 18.3c for an alternative characterization of linear dependence.)

Lemma 18.1If F is a differentiable transformation defined by Eq. (18.1), and if f and g are linearly dependent, then the Jacobian of F is identically zero.

PROOF. Differentiating Eq. (18.2) yields

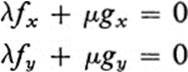
at every point of D. This is a pair of simultaneous linear homogeneous equations for the unknowns λ and μ, whose matrix is the Jacobian matrix of F at a given point of D. If the Jacobian of F were different from zero at some point, then the determinant of this system would be different from zero, and there would be a unique solution λ = 0, μ = 0. But by assumption, λ and μ are not both zero. Hence, the Jacobian must vanish at each point.

Now the notion of linearly dependent functions is a special case of the general concept of functional dependence. Intuitively, functional dependence means that there is some relation between the functions f and g. For our purposes the following definition is most appropriate.

Definition 18.2 Two functions f(x, y), g(x, y) defined in a domain D are functionally dependent if there exists a continuously differentiable function φ(u, υ) such that

1. φ(f(x, y), g(x, y)) ≡ 0.

2. ∇φ ≠ 0 at each point (u, υ) = f(x, y), g(x, y)) for (x, y) in D.

RemarkGeometrically, functional dependence has the following interpretation. Condition 1 means that the transformation F defined by Eq. (18.1) maps the domain D into the set of points satisfying φ(u, υ) = 0, and Condition 2 tells us (by the implicit function theorem) that this set of points lies on a regular curve (Fig. 18.1). (See the note in Ex. 18.5b for further comments on the definition.)

Example 18.1

Here Condition 1 is just Eq. (18.2), and Condition 2 says that not both λ and μ are zero, so that f and g are linearly dependent.

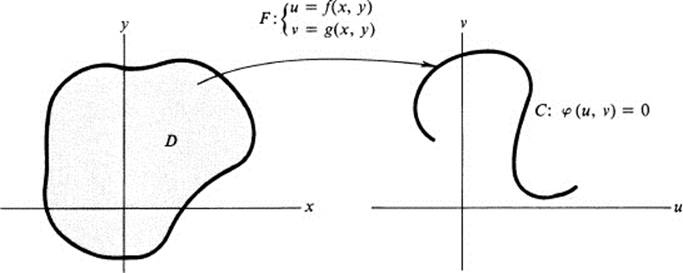
FIGURE 18.1 Geometrical interpretation of functional dependence

Example 18.2

Let

Then

This means that Condition 1 is fulfilled if we set

Condition 2 is also fulfilled, since

Thus xy and 1 + x²y² are functionally dependent.

Theorem 18.1 Let F be a differentiable transformation defined by Eq.(18.1) . If f(x, y) and g(x, y) are functionally dependent, then the Jacobian of F is identically zero.

PROOF. If we differentiate the equation of Condition 1, using the chain rule, we find

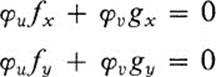
at every point. Using Condition 2, the reasoning of Lemma 18.1 may be applied without change.

It is natural to ask whether the converse of Th. 18.1 is true. If the Jacobian of a mapping vanishes identically, does that imply functional dependence? The answer is that this is more or less true, but not without qualifications. Rather than go into detail, we may summarize the situation as follows. Given a pair of functions f(x, y), g(x, y), which we should like to test for functional dependence, the first step is to compute the Jacobian. If the Jacobian is notidentically zero, then f and g are not functionally dependent by Th. 18.1. On the other hand, if the Jacobian is identically zero, then this is strong evidence of functional dependence, and the best procedure is to try to find an explicit relationship between the functions. (See also the Remark preceding Ex. 18.27.)

Example 18.3

Let

Are these functionally dependent?

We start by finding the Jacobian,

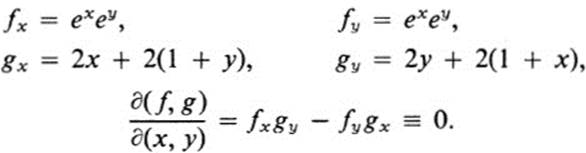
Thus we are led to seek a functional relationship. By elementary manipulations we can rewrite f and g in the form,

Thus

so that f and g are funcionally dependent.

Diffeomorphisms and Conformal Mappings

The transformations whose Jacobians are identically zero are in a sense the “most singular” of all differentiable transformations. Every point is a singular point, and in general, a whole domain is mapped into a curve. At the other extreme, we have the class of differentiable transformations that are the “most regular.” The following terminology is now standard.

Definition 18.3 A differentiable transformation F, which maps a domain D one-to-one onto a domain E and whose Jacobian is never equal to zero, is called a diffeomorphism.

Remark Since the map F of D onto E is one-to-one, there is an inverse map G of E onto D. By Th. 17.3 the map G is also differentiable. One sometimes uses the property that F and F⁻¹ are differentiable as the definition of a diffeomorphism.

We conclude our discussion of differentiable transformations by studying a special class of diffeomorphisms that arises in several important connections—the “angle-preserving” transformations. We first make precise the notion of angle between two curves.

Definition 18.4 If two regular curves pass through a point (x₀,y₀), then the angle between the curves at (x₀, y₀) is defined to be the angle between their tangent vectors at the point.

Example 18.4

Find the angle between the curves

at the point (0, 2).

We first find on each curve the value of the parameter t that corresponds to the point (0, 2). In both cases it is t = 1. For C₁ we have

and for t = 1 the tangent vector is

For C₂ we have

and at t = 1 the tangent vector is 4, 0 . If θ is the angle between these tangent vectors, then

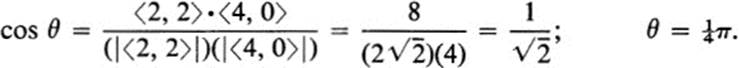
Definition 18.5 A Conformal mapping is a diffeomorphism that preserves all angles between curves.²

Remark To be precise, if F is a diffeomorphism that maps a domain D onto a domain E, then every regular curve in D is mapped onto a regular curve in E (see Ex. 16.16). To be a Conformal mapping the following must hold. Let (x₀, y₀) be any point in D, and (u₀, υ₀) its image point in E. For every pair of regular curves through (x₀, y₀), the angle between these curves at (x₀, y₀) must equal the angle between the image curves at (u₀, υ₀).

Theorem 18.2 A diffeomorphism F: (x, y) → (u, υ) is a Conformal mapping if and only if one of the following pairs of equations holds throughout D,

or

PROOF. Let (x₀, y₀) be any point of D. The differential dF_{(x0, y0)} defines the correspondence between tangent vectors to curves at (x₀, y₀) and their images. Thus angles between curves at (x₀, y₀) are preserved under F if and only if dF_{(x0, y0)} preserves angles. But dF_{(x0, y0)} is a linear transformation with matrix

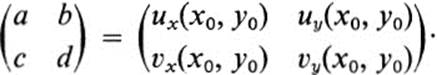
By Th. 15.3, dF_{(x0, y0)} preserves angles if and only if it is a similarity transformation, and by the Corollary to Th. 15.2 the algebraic condition for this is precisely that either a = d and b = − c, or else a = −d, b = c. Thus F is Conformal if and only if at each point (x₀, y₀) either (18.3) or (18.4) holds. Note that if (18.3) holds, the Jacobian is positive, while for (18.4) it is negative. Since the Jacobian of a diffeomorphism is never zero, and since the Jacobian is a continuous function in D, it must be either everywhere positive or everywhere negative (see Ex. 5.14). Thus either (18.3) or (18.4) must hold throughout D.

RemarkThe term conformal is sometimes reserved for transformations satisfying (18.3) that preserve orientation (since the Jacobian is positive), while a mapping satisfying (18.4), which necessarily reverses orientation, is called anticonformal. This is especially true in the study of functions of a complex variable, where one is led to Eqs. (18.3). In that context these equations are called the Cauchy-Riemann equations. It is clear from our derivation that these equations are no more nor less than the algebraic condition on the Jacobian matrix at each point that the differential dF be a similarity transformation preserving orientation.

Example 18.5

Let F be the transformation

which we examined in detail at the end of Sect. 13.³ From the description we gave there it is clear that F maps the first quadrant one-to-one onto the upper half-plane υ > 0. The Jacobian matrix is

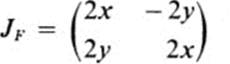
so that Eqs. (18.3) are satisfied, and the Jacobian is equal to 4(x² + y²), which is different from zero in the first quadrant. Thus F is a Conformal mapping of the first quadrant onto the upper half-plane. (The same would be true for any quadrant, or more generally, any domain D in the x, y plane in which the map F is one-to-one.) Note in particular that the curves x² − y² = c and 2xy = d indicated in Fig. 13.12 must intersect at right angles, since they map onto the perpendicular lines u = c, υ = d. This gives an example of “orthogonal families of curves.” Namely, the set of curves x² − y² = c, for different values of c, forms one family of curves, and the curves 2xy = d, as d varies, form a second family (see Fig. 18.2). What we have seen is that each curve of the first family intersects each curve of the second family at right angles. This could also be verified by noting that these families are level curves of the functions x² − y² and 2 xy, and the gradients of these functions are the vectors 2x, −2y and 2y, 2x , respectively, which are perpendicular vectors at each point.

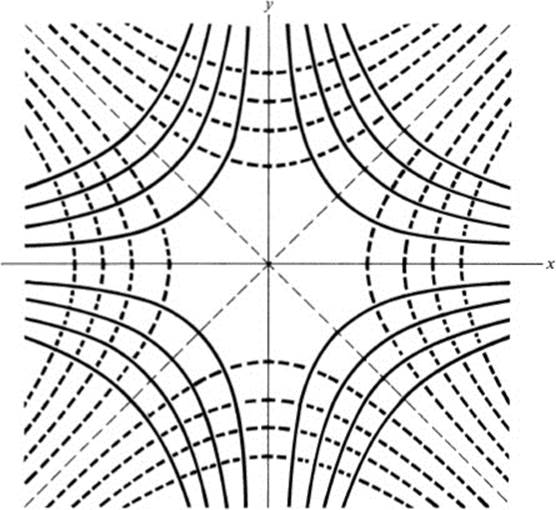
FIGURE 18.2 Orthogonal families of hyperbolas

Exercises

18.1Test each of the following pairs of functions for functional dependence. (The domain D is the whole plane except in parts a, e, and g, where D is taken to be the first quadrant.) In case of functional dependence, give an explicit relationship of the form φ(u, υ) = 0.

a.

b.

c.

d.

e.

f.

g.

h.

i.

*j.

18.2Which pairs of functions in Ex. 18.1 are linearly dependent?

18.3 a. Show that if one function of a pair is identically zero, then the pair of functions is linearly dependent.

b. Show that if a pair of functions is linearly dependent, and if neither function is identically zero, then each function equals a constant times the other function.

c. Using parts a and b, show that f(x, y) and g(x, y) are linearly dependent if and only if either f(x, y) ≡ cg(x, y) or g(x, y) ≡ cf(x, y) for some constant c (which may be zero).

18.4 a. Let h(t) be a continuously differentiable function of one variable. Show that if g(x, y) ≡h(f(x, y)), then f(x, y) and g(x, y) are functionally dependent.

*b. Let f(x, y) and g(x, y) be functionally dependent in a domain D. Let (x₀, y₀) be any point of D. Show that there exists some r > 0 and there exists a continuously differentiable function h(t) such that for

either

18.5Let

a. Show that ∂(f, g)/∂(x, y) ≡ 0.

b. Show that although [f(x, y)]³ ≡ [g(x, y)]², this does not imply that f(x, y) and g(x, y) are functionally dependent in the whole plane according to Def. 18.2, since the function φ(u, υ) = u³ − υ² has zero gradient at the origin.

(Note: the definition of functional dependence is sometimes enlarged to allow dependence of this sort, but then a different proof is needed for Th. 18.1. Sometimes functional dependence is defined by the vanishing of the Jacobian, but that does not imply a functional relationship in the sense we envisage intuitively. See, however, Ex. 18.27, and the remark immediately preceding it.)

18.6 a. Let F(t), G(t) be continuously differentiable functions of one variable, and let f(x, y) = F(h(x, y)), g(x, y) = G(h(x, y)), where h(x, y) ∈ in some domain D. Show that ∂(f, g)/∂(x, y)≡ 0 in D.

b. Give a geometric description of the mapping u = f(x, y), υ = g(x, y) in part a.

18.7Find the angle between each of the following pairs of curves at the point indicated.

a. C₁: x = t, y= t; C₂:x = t, y = /t, at (1, )

b. C₁: x = e^t, y = 2 + 4 sin t; C₂:x = t⁴, y = t + 3; at (1, 2)

c. C₁: x = log(l + t²), y = e^t + e^−t;

C₂:x = t³ − t, y = t² + t; at (0, 2)

18.8Decide whether each of the following transformations is a diffeomorphism or not in the domain indicated. For those that are diffeomorphisms, use Th. 18.2 to test for conformality.

a.

b.

c.

d.

e.

f.

g.

*h.

*i.

18.9Consider the transformations

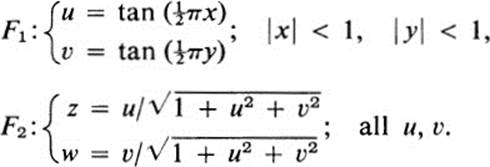
a. Show that F₁ is a diffeomorphism of the square |x| < l, |y| < 1 onto the whole plane.

b. Show that F₂ is a diffeomorphism of the whole plane onto the disk u² + υ² < 1.

c. Show that F₂ F₁ is a diffeomorphism of the square onto the disk.

*d. Is F₂ F₁ Conformal?

18.10Let F₁ be a diffeomorphism of a domain D onto a domain E. Let F₂ be a diffeomorphism defined on E.

a. Show that F₂ F₁ is a diffeomorphism.

b. Show that if F₁ and F₂ are both Conformal, then so is F₂ F₁.

*c. Do part b using Th. 18.2.

18.11 Let F be a diffeomorphism.

a. Show that F⁻¹ is a diffeomorphism.

b. Show that if F is Conformal then F⁻¹ is conformal.

c. Do part b using Th. 18.2.

18.12Show that a linear transformation is a Conformal mapping if and only if it is a similarity transformation.

18.13Show that if a Conformal mapping of a domain D is given by u = f(x, y), υ = g(x, y), then f(x, y) and g(x, y) are harmonic functions in D.

18.14Show that a diffeomorphism given by u = f(x, y),υ = g(x, y), where f(x, y) and g(x, y) are harmonic functions, need not be Conformal. (Hint : consider linear transformations.)

18.15 a. Show that if a diffeomorphism F of a domain D is a Conformal mapping, then at each point (x₀, y₀) D, the vectors

and

satisfy

b. Interpret the condition of part a geometrically in terms of the action of F on horizontal and vertical lines.

c. Show that if a diffeomorphism F satisfies the condition of part a at every point of a domain D, then F is a Conformal mapping. (Hint; use the Corollary to Th. 15.2.)

18.16Let F be a diffeomorphism defined by u = f(x, y), υ = g(x, y) in a domain D.

a. Show that if F is Conformal, then at each point of D,

b. Show that if F is Conformal, then

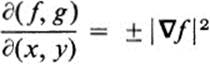
at each point of D.

c. Show that if F is Conformal, then f and g satisfy the conditions

at every point of D.

*d. Show that if f and g satisfy the conditions of part c at each point of D, then F is conformal. (Hint: adapt the reasoning used in the proof of Th. 15.2 to get from Eqs. (15.16) to (15.17).)

18.17Show that if F is a diffeomorphism of a domain D and if the Jacobian of F is positive at each point of D, then F is a conformal mapping if and only if at each point (x₀, y₀) of D the differential dF_{(x0, y0)} consists of a dilation by some constant λ > 0 followed by a rotation. (Note that the value of λ and the amount of rotation will, in general, vary from point to point.)

18.18Show that if F is a diffeomorphism of a domain D and if the Jacobian of F is negative throughout D, then the transformation H = G F, where G is a reflection in the horizontal axis, is a diffeomorphism with positive Jacobian.

Note: it follows that every Conformal mapping is either of the form described in Ex. 18.17, or else consists of a transformation of that form followed by a reflection. This characterization of Conformal mappings, in terms of the action of dF at each point, provides probably the deepest insight into their nature. Thus, Fig. 16.5, which illustrates a special case, gives a valid picture of the general situation.

*18.19 Let F be a diffeomorphism defined by u = f(x, y), υ = g(x, y). Let (u₀, υ₀) = F(x₀, y₀). Let C be a regular curve passing through (x₀, y₀) and let Γ be the image of C under F. Let s be the parameter of arc length on C and let σ be the parameter of arc length on Γ. If C is written in the form x(s), y(s) , using the arc length s as parameter, then Γ takes the form:

Let

where (x(s₀), y(s)) =(x₀, y₀).

a. Show that | X, Y | = 1, | U, V | = dσ/ds, evaluated at s₀.

b. Show that U, V = dF_{(x0, y0)}( X, Y ).

c. Using parts a and b, show that dσ/ds depends only on the tangent direction of the curve C at (x₀, y₀).

(Note : since dσ/ds is equal to the rate of change of arc length along Γ with respect to arc length along C, and since this “ratio of arc lengths” depends only on the tangent vector X, Y to C, we may call it the dilation of the mapping F at the point (x₀, y₀) in the direction of X, Y .)

d. Show that U² + V² is equal to a quadratic form in X and Y, and find the coefficients.

e. Let λ₁ and λ₂ be the maximum and minimum of the dilation of F at the point (x₀, y₀) as X, Y ranges over all unit vectors (that is, λ₁ and λ₂ are the maximum and minimum of dσ/ds as C ranges over all regular curves through (x₀, y₀)). Show that and are the maximum and minimum of the quadratic form in part d.

f. Show that the quantities λ₁ and λ₂ of part e satisfy

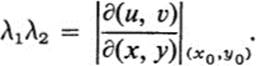
g. Show that λ₁ = λ₂ if and only if dF is a similarity transformation.

h. Show that F is a Conformal mapping if and only if the dilation of F at each point (x₀, y₀) is independent of the direction (that is, the quantity dσ/ds is the same for all curves C passing through (x₀, y₀)).

18.20Note that the mapping u = x² −y², υ = 2xy satisfies the Cauchy- Riemann Equations (18.3) at every point of the plane. However, according to our description of this mapping in Sect. 13, two lines through the origin map onto two lines through the origin in such a way that the angle between the lines is doubled. Explain why this does not contradict Th. 18.2.

18.21Let D be the quarter disk x > 0, y > 0, x² + y² < 1. Let E be the half disk υ < 0, u² + υ² < 1.

a. Show that the equations u = x² − y², υ = 2xy define a Conformal mapping of D onto E.

b. Note that the right angle at the origin in D maps onto a straight angle at the origin in E. Explain why this does not contradict part a.

18.22The equation υ² = 4c²(c² − u) represents, for an arbitrary constant c ≠ 0, a parabola with focus at the origin and opening to the left. As c runs through all positive real numbers we obtain a family of confocal parabolas. Similarly, the equation υ² = 4d²(d² + u) describes, for arbitrary d ≠ 0, a parabola with focus at the origin opening to the right. Show that every such parabola meets every parabola of the first family at right angles. Illustrate with a sketch. (Hint: consider the images of horizontal and vertical lines under the transformation u = x² − y², υ = 2xy.)

18.23 a. Show that a diffeomorphism F: (x, y) → (u, υ) has the property that the images of each pair of lines x = c,y = d intersect at right angles if and only if u_xu_y + υ_xυ_y = 0.

b. Give examples of transformations that satisfy the condition in part a and are not conformal.

c. Let F = (x, y) → (u, υ) be a transformation satisfying the condition in part a, and let C:(u, y) → (z, w) be conformal. Show that G F satisfies the condition in part a.

18.24 Show that a diffeomorphism is a Conformal mapping if and only if every pair of perpendicular lines map onto curves that intersect at right angles. (.Hint: apply Th. 15.3.)

18.25 Show that the curves x³ − 3xy² = c, where c Φ 0, and 3x² y − y³ = d, d Φ 0, intersect at right angles.

18.26 Show that the two families of curves

and

are orthogonal families; describe the curves of each family and sketch several of them. (Hint: consider the mapping: u = x/(x² + y²), υ = y/(x² + y²).)

RemarkThe following result may be considered as a partial converse of Th. 18.1: Suppose f(x, y), g(x, y) ∈ in a domain D and ∂(f, g)/∂(x, y) ≡ 0 in D. If f_y(x₀, y₀) ≠ 0, then there is a function F(t) of one variable such that for all(x, y) in some disk (x − x₀)² + (y − y₀) < r², g(x, y) = F(f(x, y)). For a proof, see [36], Sect. 12.3. Exercise 18.27 is intended to give some insight into why such a result might be expected to hold.

*18.27Let F be defined in a domain D by u = f(x, y), υ = g(x, y), where ∂(u, υ)/∂(x, y) ≡ 0.

a. Show that at any point where u_y ≠ 0, there exists a number λ such that ∇g = λ∇f.

b. Show that the image under F of a curve C:x(t), y(t), is the curve Γ:u = f_c(t), υ = g_c(t), and that at a point where u_y ≠ 0, = where λ is the same as in part a.

c. Show that if C is a level curve f(x, y) = u₀, and if u_y ≠ 0 at each point of C, then and g(x, y) is constant along C.

d. Show that if C is a segment of a vertical line x = x₀ and if u_y ≠ 0 along C, then the curve Γ : u = f(x₀, y), υ = g (x₀, y) can be expressed in non- parametric form as υ = F(u). (Hint : the equation u = f(x₀, y) can be solved for y in terms of u.)

Remark (continued) The remainder of the argument may be pictured intuitively as follows. If u_y(x₀, y₀) ≠ 0, then by continuity, u_y ≠ 0 in some disk (x − x₀)² + (y − y₀)² < r².Let u₀ = f(x₀, y₀), υ₀ = g(x₀, y₀). By part d, the segment x = x₀, y₀ − r ≤ y ≤ y₀ + r maps onto a curve υ = F(u) through (u₀, υ₀). Each point (u₁, υ₁) of this curve is the image of a point (x₁, y₁) in the disk, and since u_y(x₁, y₁) ≠ 0 we may apply the implicit function theorem to deduce that the level curve f(x, y) = u₁ through (x₁, y₁) is a regular curve C. By part c, g(x, y) ≡ υ₁ on C. Thus the curve C is the inverse image of the single point (u₁, υ₁), and the inverse image of each point on υ = F(u) is a whole curve. This gives a family of curves each of which maps onto a point of υ = F(u). (Note the analogy with the behavior of linear transformations whose determinant is zero, as described in Ex. 14.5c.) All that remains to complete the proof is to show that this family of curves fills out some disk about the point (x₀, y₀), and that can be done by slightly more refined arguments.