Two-Dimensional Calculus (2011)

Introduction

Examples of functions of several variables are encountered at every turn in mathematics and its applications. By way of illustration, consider the following.

Algebra

1. The expressions for the roots of the general quadratic equation ax² + bx + c = 0

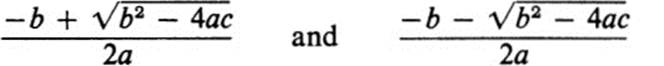
represent functions of the three variables a, b, c.

2. The simultaneous linear equations

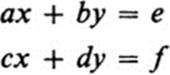
have a determinant

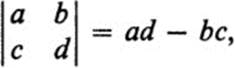
which is a function of four variables.

For three equations in three unknowns, the corresponding determinant is a function of nine variables.

Trigonometry

1. The “addition formula” for the sine of a sum of two angles is given by the expression

which is a function of two variables.

2. The cosine law for a triangle

gives c as a function of the three variables a, b, C.

Geometry

1. he distance from the point (X, Y) to a fixed line ax + by + c = 0 is

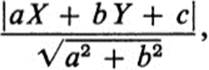
which is a function of the two variables X, Y.

2. The volume of a cylinder of height h and elliptical base is

which is a function of the three variables a, b, h.

Calculus of One Variable

1. For a given differentiable function f(x) the equation of the tangent line to the curve y = f(x) at x = x₀ is

a function of the two variables x₀ and X.

2. For a fixed continuous function f(x), the definite integral

is a function of the two variables a and b.

It is quite true that in most of these examples we tend to regard the expressions as “formulas” involving certain constants, rather than “functions” involving certain variables. Thus, in the last illustration, the definite integral is defined by considering a and b as having fixed values. However, the whole theory of integration is based on the fundamental theorem of calculus, which is derived precisely by allowing the limits of integration to vary, and observing the change in the value of the integral, considered as a function of the variable endpoints.

Again, the formula for the distance from a point to a line can be much more easily derived, as we shall show, by allowing the point to vary, and considering the distance to be a function of the variable coordinates, rather than by the usual static approach using a fixed point and a fixed line.

If we turn to the functions that arise in physical applications, we find that they are almost invariably functions of more than one variable. For example, temperature and pressure in a gas (such as the earth’s atmosphere) are, in general, functions of the four variables x, y, z, t, where x, y, z are the coordinates of position in space, and t represents time.

In view of the fact that “almost all” the functions we encounter seem to involve more than one variable, we may wonder how the calculus of functions of a single variable is at all applicable. One answer is that a function of several variables can always be artificially reduced to be dependent upon a single variable by fixing all the other variables. Thus we may consider the variation of temperature at a given instant of time along a vertical line above a point on the earth’s surface. The temperature then becomes a function of the single variable height. Or we may consider the variation of temperature with time at a fixed point in space.

The question is how satisfactory a description of the entire function do we obtain by this process of studying it separately with respect to each variable? A brief answer is that in some cases we get an adequate description, while in others this approach fails completely. From the mathematical point of view, there are a number of new and important concepts that arise when we allow the variables to vary simultaneously. These will be discussed in detail in Chapter 2. From the physical point of view, the artificiality of holding all but one variable fixed can be realized from the example of measuring the temperature along a vertical line. As we move along the line and take readings, the time is in fact varying too. Although this may seem to be a purely practical difficulty rather than a theoretical one, it was pointed out by Einstein in his first paper on relativity that basic problems arise in trying to define what is meant by “the same time” in different places.¹

Without going as far afield as relativity, let us consider a very concrete physical problem. If a sound is emitted underwater, what path does it take? It is known, just as in the case of light, that the path is not a straight line but is refracted if the velocity is not constant. The velocity of sound underwater (in meters per second) is given approximately by the following formula²:

where T is temperature in degrees centigrade, D is depth in meters, and S is salinity in parts per thousand. Note that each of the variables T, D, S is itself a function of the four variables x, y, z, t. As we move along the path of a “sound wave,” the variables x, y, z, t are all changing. They, in turn, determine the values of T, D, S, which determine the velocity. A typical question that we may encounter is the following: if T, D, and S are not known explicitly as functions of x, y, z, t, but if we have determined their values at some point and their rate of change in various directions, can we determine the rate of change of the velocity υ in an arbitrary direction?

The purpose of this book is to provide the basic tools for treating problems of this general nature. We may note that an important feature of the above problem is that we have to consider a whole set of functions of several variables. We shall see later (Chapter 3) that although some information may be derived by considering each function separately, there are important advantages to be gained from dealing with the set of functions simultaneously.

In its most general form, the subject introduced in this book may be described as the study of systems of functions of several variables :

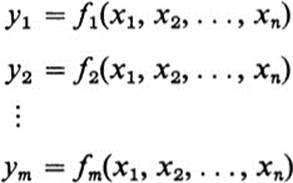
Here we have n variables, denoted as x₁, ...,x_n, and m functions, f₁, ..., f_m.

Our approach will be to gradually increase the number of variables and functions to be considered. We shall also find a variety of ways in which we may reduce a problem to the consideration of a function of a single variable, to which we may then apply the results of elementary calculus.

A final word concerning theorems and their proofs. The statements of theorems comprise the core of basic information about the subject matter. You should make every effort to understand the meaning of each theorem. Many examples and comments are given to assist you in acquiring this understanding. You should also attempt to follow the reasoning in the proofs of the theorems. In some cases the proofs will help shed light on the content of the theorem. There are some cases, however, where a proof will be too difficult to understand fully on a first reading. Only by reading subsequent sections and then returning to the proof will you be able to grasp completely the material. We are dealing here with a fundamental and almost paradoxical difficulty. Stated briefly, it is that learning is sequential but knowledge is not. A branch of mathematics (or any other body of knowledge) consists of an intricate network of interrelated facts, each of which contributes to the understanding of those around it. When confronted with this network for the first time, we are forced to follow a particular path, which involves a somewhat arbitrary ordering of the facts. It is the large degree of choice in the path to be followed that accounts for the many different presentations possible for a given subject. One can be a very efficient tourist and race from one landmark to the next, or one can stop to investigate interesting side paths. One can choose between direct routes and scenic routes. One can enjoy the happy glint of recognition when an earlier point on the path is approached from a new direction.

This book has been arranged in a way intended to provide a path that affords a commanding view and at the same time a firm foothold for the student first discovering his way through the intricacies of higher-dimensional calculus. You are urged to make repeated return trips over parts of the path that have already been traveled ; you will surely be happily surprised at how much easier it is to traverse the same stretch the second time, and at how often what at first seemed only a confused tangle of underbrush later assumes a clearly defined form and pattern. This transformation from an amorphous to a crystalline structure is a process that must take place inside each individual. Besides being an esthetically satisfying experience, it is the only process that can be truly called learning.

¹ See, for example, reference [20]. Still better, see Einstein’s original paper on relativity ([15], 37–65), and in particular, Sections 1 and 2, dealing with the definition of simultaneity and the relativity of lengths and times. We may note that there is a widespread misconception that advanced mathematical training is required in order to approach the theory of relativity. As a matter of fact, high school algebra is all that is needed to understand the two sections referred to above, and Einstein’s entire paper uses no mathematical concepts beyond those discussed in the first three chapters of the present book.

² For more precise versions of this formula, see references [4] and [26].