University Mathematics Handbook (2015)
V. Integral Calculus of Single-Variable Functions
Chapter 2. Definite Integral
2.1 Definition
Let 
be a function defined on interval 
. Let's divide interval 
into subintervals by the points
We denote 
, using the same denotation for the length of all subintervals, 
, 
.
Let us denote 
. In every 
, we select an arbitrary point 
. The expression
is called Riemann sum, according to the partition to subintervals and the selected points .
Definition: function is called a Riemann integrable function, on interval , if the limit 
exists and is not dependent on the selection of partitions and points . We denote this limit by 
, and it is called the definite integral of function on interval , when 
and 
in integral 
are called limits of integration.
2.2 Classes of Integrable Functions
a. If function is not bounded on interval , then it is not integrable on that interval.
b. If function is continuous in interval , then it is integrable in it.
c. A function defined and bounded in interval is called piecewise continuous function, if it has at most a finite set of discontinuities, all of which are jump discontinuities.
d. If function is piecewise continuous in interval , then it is integrable in it.
2.3 Properties of Definite Integral
a. 
b. 
c. 
for every constant 
d. 
e. If 
, then 
, particularly when 
, 
.
f. If and 
are integrable on , then 
is integrable on interval .
g. Mean Value Theorem for Integrals
If is continuous on , then there is a point on , such that
The number 
is called the average value of on .
h. If 
for all 
, then 
.
i.
1. If is integrable on , then 
is also integrable in that interval and there holds 
.
2. The inverse is incorrect. That is, if is integrable, it doesn't necessarily follow that is integrable in that interval.
j. If 
and 
for all , then
2.4 Connection Between the Indefinite and Definite Integral
If is a continuous function and 
is its antiderivative on , then:
a. 
, when 
b. 
c. Newton-Leibniz Formula 
d. 
e. Cauchy-Schwartz Inequality
If and are integrable on , then:
2.5 Calculating Definite Integrals
a. Change of Variables
If function is continuous on , and if function 
is continuously differentiable on 
, if its image equals interval , and there holds 
and 
, then:
b. Integration by Parts
If functions 
and 
have continuous derivatives on , then:
c. Integral of Even and Odd Functions on Interval 
If function is even and integrable on , then:
And, if function is odd and integrable on , then:
2.6 Numerical Methods of Computing Definite Integrals
We divide interval into 
equal sub-intervals, by points:
when 
, .
a. The following formulas are rectangle approximations:
when is the midpoint of 
.
The approximation error, in the case that is twice differentiable is 
.
b. Trapezoid Approximation
The approximation error is 
c. Simpson's Rule
when is then midpoint of 
.
The approximation error is
2.7 Applications of Definite Integral
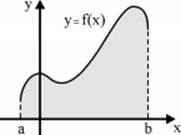
a. The area of a plane confined by the graph of non-negative function , 
-axis, and straight lines 
and 
is
b. The Area of a plane bounded by a curve presented in the parametric form 
is
c. The area of a plane bounded by two functions , 
, above interval is
d. The area of a plane bounded by a curve presented by 
, 
, and two rays, 
and 
is
e. The length of a planar curve given by:
1) 
, is 
2) 
, 
is 
f. The volume of a solid of revolution around the 
-axis of an area confined by the graph of non-negative function and the straight lines , , is
g. The volume of a solid of revolution around the -axis of an area confined by the graphs of functions and and straight lines , , is
h. The volume of a solid of revolution around the 
-axis of an area confined by the graph of non-negative function and the straight lines , , is
i. The volume of a solid of revolution around the -axis of an area confined by the graphs of functions and in interval is
j. If a solid body is confined by planes , , and the plane 
carves out of the body an area 
for every 
, then, the volume of the body is
Example: Calculate the volume of the sphere 
, confined between the planes 
and 
.
For every situated at 
, the section is circle 
, the area of which is 
. Therefore, the volume of the sphere is
