University Mathematics Handbook (2015)

VI. Series

Chapter 1. Basic Concepts

1.1  Series of Numbers. Summation of Series

a.  Let be a sequence of numbers.

The expression is called infinite series or just a series, and a_k is the general term of the series.

The terms of the series add up to partial sums:

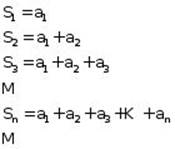
The result is a sequence of partial sums .

b.  Series is convergent if there exists a finite limit of the sequence of partial sums . is called the sum of the series. Written .

If the limit of does not exist, or is infinity, the series is called divergent.

c.  Examples:

1.  Geometric Series

converges if and only if and its sum is .

2.  Leibniz Series

3.  Series is divergent.

4.  Harmonic Series .

1.2  Series Remainder

The series is the -th remainder of the series , .

1.3  Telescoping Series

a.  Let be a sequence of numbers. Series is called telescoping series.

b.  A telescoping series is convergent if and only if sequence is convergent.

c.  If sequence converges to , then the sum of the telescoping series is .

1.4  Properties of Convergent Series

a.  Cauchy's Criterion: Series converges if and only if

, , ,

b.  Necessary Condition of Convergence

If series converges, then .

This is an insufficient condition: For instance, for harmonic series , there holds , yet the series is divergent.

c.  If series is convergent, then the sequence of remainders converges to zero. That is, for every there exists such that for all , there holds .

1.5  Operation on Series

a.  Removing a finite number of terms from a series, or adding a finite number of terms to it, does not affect the convergence or divergence of the series.

Attention: It does change the sum of the series.

b.  If converges to , then, for every constant the series converges to .

If series is divergent, then, for all , the series , is divergent.

c.  If series , are convergent, then, the series is convergent, and .