University Mathematics Handbook (2015)

VII. Differential Calculus of Multivariable Functions

Chapter 3. Limits and Continuity of Functions

3.1  Definition of Limit

a.  Cauchy's Definition: is the limit of function at the point , if for every there exists , such that for all holding , there holds . It is written .

b.  Limit is not dependent of the path through which point tends to .

c.  Heine's Definition: is the limit of function when , if for all sequences of points converging to and where the function is defined, the sequence converges to .

d.  Cauchy's and Heine's definition of limit are equivalent.

3.2  Properties of Limit

Let and be functions defined at the point . If the limits exist, then:

a.  

b.  

c.  If, in addition, and , then: .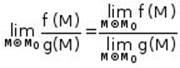

3.3  Continuity at a Point

Function is continuous at point if for every there exists such that for all holding there holds .

In other words, function is continuous at if .

3.4  Properties of Continuous Functions

a.  If function is continuous on and , , then there exists a neighborhood of such that at all point of that neighborhood, , .

b.  If functions and are continuous on , then:

1.  Functions , are continuous on _.

2.  If, in addition, , then, function , is continuous on .

c.  Continuity of a Composite Function

Theorem: Let be a function defined by , and functions

(*)

defined by and let be a point on and a point on , the coordinates of which are connected by (*).

If functions are continuous on and function is continuous on , such that

, then, the composite function is continuous on .

In other words, a composition of continuous functions is a continuous function.

d.  Function is continuous on domain if it is continuous on all points of .

e.  Intermediate Value Theorem: If function is continuous in connected domain , and if points are on , then, for all real number between and there exists point such that .

f.  Weierstrass Theorem: If function is continuous on closed and bounded domain , then it is bounded on that domain, reaching its maximum and minimum value above . That is, there exist points , on , such that:

3.5  Uniform Continuity

a.  Function is continuous on domain if, for every there is , dependent on , such that for all two points which hold , there holds .

b.  Cantor Theorem: If function is continuous on closed and bounded domain , then it is uniformly continuous on that domain.