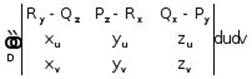University Mathematics Handbook (2015)

IX. Vector Analysis

Chapter 10. Surface Integral

10.1  Surfaces

a.   is a smooth surface if vector function is of class region.

b.  The unit normal to surface is

c.  A smooth surface S is called oriented (two-sided) if there is a normal unit vector n at every point on S, not on the boundary curve of S, such that n is a continuous function of (x, y, z) on S. Later on, each surface must be oriented, have a finite area and a single smooth, closed boundary curve. The sphere, ellipsoid, paraboloid, and hyperboloid are two-sided surfaces.

A nonorientable surface is, for example, a Mobius strip. It is formed by half-twisting a strip of paper, attaching its ends together (see illustration). If we draw a unit normal N from one point of a Mobius strip, we eventually get a normal at the same point, at the opposite direction of the original normal.

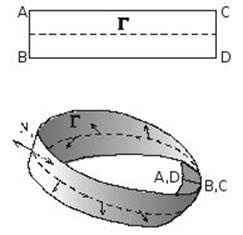
d.  A smooth surface is two-sided if the direction of normal can on it can be specified definitely. Later on, we shall only refer to two-sided surfaces.

e.  The area of the surface is .

f.  If surface is given in the form , then its area is .

g.  The positive direction of surface is the direction of normal . If is the boundary of a closed body, then the positive direction on is outwards. If is an open surface, then the positive direction is towards the Z-axis.

10.2  Surface Integral

Given a vector field

a.   is a surface integral when is the unit normal vector to surface .

b.  Different ways of writing and calculating surface integral:

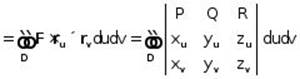
when are directional angles of .

c.  Gauss Divergent Theorem

Let be a body the boundary of which is smooth and closed surface with an outer normal . If vector field is of class in , then holds

or .

The integral is called the flux of vector field through surface .

d.  Stokes Theorem

If, in the neighborhood of two-sided surface , vector field is of class and is the boundary of surface in the positive direction, then

or

denote