University Mathematics Handbook (2015)

X. Algebra

Chapter 13. Inner Product Spaces

13.1  Inner Product

a.   is an inner product space over field if every ordered pair of vectors has a corresponding number of called the inner product of vectors and and denoted such that:

1.  

2.  

3.  

4.   for every .

b.  If is a field of complex numbers , then is a unitary space.

c.  If is a field of real numbers , then is a Euclidean space.

d.  In a Euclidean space, .

e.  Every finite-dimensional vector space over fiend is unitary.

f.  Examples:

1.  Vector space with inner product .

2.  A space of continuous real functions on interval with the inner product is a Euclidean space.

3.  Complex matrices space is a unitary space with the inner product

4.   is the space of all infinite sequences such that the series is convergent. The inner product of two vectors of is

13.2  Cauchy-Schwartz Inequality

a.  Non-negative number is called a length or a norm of vector .

b.  For every vectors of a unitary space, there holds:

This equality holds if and only if and are linearly dependent.

c.  In a continuous functions space (see example f.2), Cauchy-Schwartz inequality is in the form of

d.  Triangle inequality: The length of sum of two vectors is no greater than the sum of their lengths. That is, , and this equality holds if, and only if, (that is, and are parallel and in the same direction).

e.  Angle between non-zero vectors of vector field is defined by .

f.  Angle exists and is unique.

13.3  Orthogonality

a.  Vectors and of unitary space are orthogonal (perpendicular) if their inner product is equal to zero, that is, .

b.  Vector is the only vector that is orthogonal to any other vector of .

c.  Set of vectors of unitary space is orthogonal if any two different vectors of are orthogonal.

d.  An orthogonal set of non-zero vectors is linearly independent. If, in addition, it spans the space, then it is an orthogonal basis in span .

e.  Gram-Schmidt theorem: every -dimensional unitary space has an orthogonal basis. Moreover, for every linearly independent set spanning a subspace , there is an orthogonal set spanning .

f.  Gram-Schmidt orthogonalization: If is linearly independent set, we construct a set of orthogonal non-zero vectors such that for every , the following way:

1.  Define .

2.  Choose such that is orthogonal to .

The result is .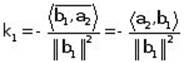

Therefore, .

The same way we get

13.4  Orthonormal Basis

a.  An orthogonal vector set is orthonormal if every vector of the set is normalized (that is, it has a unit length).

b.  Every unitary space has an orthonormal basis.

c.  In unitary space , the components of a vector in orthonormal basis are

d.  If is a basis in unitary space and , are two vectors of , then basis is orthonormal if and only if the inner product of every two vectors and is .

13.5  Fourier Coefficients

a.  Let orthonormal basis in unitary space and . Scalars are called Fourier coefficients of in respect to .

b.  Let be an inner product space and . The distance between and is non-negative number .

c.  If is an orthonormal system in vector space and , then vector is the closest vector to of . Moreover, is the unique vector of at a minimum distance from .

d.  Bessel's Inequality: If is an orthonormal system on , then, for every vector there holds:

Equality holds if, and only if, .

This is called Parseval's equality.

13.6  Infinite Orthonormal System

Let be an inner product space and an infinite orthonormal system.

a.  Bessel's Inequality: for every , series converges and there holds

b.  Let be an infinite series of vectors in a normed space . This sequence is convergent in norm to vector if . Which means, for each there exists integer such that for each , holds.

c.  Definition: Let be an infinite sequence of vectors in a normed space and let be a scalar sequence. Series is said to be convergent in norm to vector , is denoted , if the partial sumssequence converges in norm to . In other words, series converges in norm to vector if .

d.  The proposition “vector w is spanned by infinite sequence means there is a matching sequence of scalars such that as m increases, the combination becomes an increasingly better approximation to vector w. The approximation between vectors in a normed space is measured by their distance, and consequently, the exact meaning of the last proposition is that for every , as small as we wish, there exists an such that for all .

e.  Definition: Let be an infinite orthonormal system in an inner product space . It is close in if for every there holds

f.  Orthonormal system is closed in inner product space if, and only if, for every vector there holds

It means that the closeness is equivalent to Parseval's equality for every vector .

g.  Orthonormal system is complete in if the only unique vector holding is zero vector .

h.  A Generalization of Parseval's Equality: If is a complete orthonormal system in inner product space , then, for every pair of vectors there holds , when and