University Mathematics Handbook (2015)

XI. Ordinary Differential Equations, or ODE

Chapter 3. Series Solutions of Second-Order ODE

3.1  Solutions Near an Ordinary Point

a. is an ordinary point of ODE

(*)

if functions and can be developed to a power series about converging at .

b. Theorem: If is an ordinary point of (*) then (*) has a solution in the form of series with a convergence radius of at least .

c. Example: Airy equation

is a regular point. We look for the solution in the form . We differentiate twice:

Substituting in the equation, we get:

Writing , shifting the indexes, we get

Equating the coefficients of the same powers of to zero, we get recursion formula

Therefore, the general solution is

3.2  Chebyshev's Equation

a. is an ordinary point. The general solution is

b. If is zero or an integer, then one solution is a polynomial. Such polynomials are called Chebyshev's polynomials.

c. , are Chebyshev's polynomials.

d. Recursion formula:

3.3  Legendre Polynomials

Legendre Equation:

a.  Its polynomial solutions are Legendre Polynomials holding the recursion formula

b.  Rodrigues formula:

c.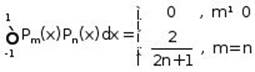  

3.4  Solutions Near a Regular Singular Point

Point is a regular singular point of ODE

(*).

If there exist finite limits

,

then the equation (**) is called the characteristic equation of (*).

a. If the characteristic equation (**) has two different real solutions, , the difference of which, , is not an integer, then (*) has two linearly independent LI solutions

b. If the characteristic equation (**) has two equal solutions , then (*) has two LI solutions

c. If and is an integer, then (*) has two LI solutions

,

3.5  Bessel's Equation

a.  The General solution, when

b.  

c.   are Bessel functions of the first kind

d.  For integer, the solutions of the equation are Bessel functions

e.  Bessel equation of order has two solutions, one unbounded in the neighborhood of , and another is zero-order Bessel function .