University Mathematics Handbook (2015)

XII. Complex Functions

Chapter 1. Complex Numbers Sequence (see X.1)

1.1  - Neighborhood

a.  A set of all points is called a
- neighborhood of complex number .

b.   is an accumulation point of set if every neighborhood of has at least one point of different from .

1.2  Limit Point of a Sequence

a.  The number is a limit of sequence , , if, for every there exists an , such than for every greater than , there holds . It is denoted , or is said, sequence converges to .

b.  Cauchy's Criteria: converges to if and only if for every there exists an , such that for every and every integer , .

Written in short:

c.  The sequence of complex numbers converges to the number if and only if the sequences of real numbers and converge to and , respectively.

d.  If complex number sequences and converge, then sequences , , and with , also converge and hold:

.

1.3  Sets in

a. is an inner point of if there exists an -neighborhood of which is entirely in .

b. is a boundary point of if in every -neighborhood of there are points of and points not of .

c. The set of all boundary points of form a boundary of set . It is denoted .

d. Set is open if it only consists of its inner points.

e. Set is closed if it includes all of its boundary points.

f. Set is closed if, and only if, it contains all of its accumulation points.

g. Set is bounded if there exists a circle of a finite radius containing it.

h. Bolzano-Weierstrass theorem: every infinite and bounded sequence of complex numbers has a subsequence converging to the limit.

1.4  Curves and Domains in

a.  A Jordan curve or a continuous curve is the set of points in the complex plane , where , are real continuous functions.

If, in addition, for every two different values , there are two different fitting points on that line except probably , , this is a simple curve.

b.  A simple curve is a smooth curve if , have continuous derivatives, which do not vanish simultaneously, that is .

c.  A continuous curve is piecewise smooth if it consists of a finite number of smooth curves.

d.  The positive direction of the curve is the parameter increase direction.

e.  Closed curve divides the plane into two domains, one not containing (an inner domain with respect to a closed continuous curve), and another, containing (an outer region with respect to the same curve). This curve is a boundary of each of these domains.

f.  A positive direction on a continuous curve is such that while we move along the curve in that direction, the inner region is always in the left.

g.  An inner region with respect to a continuous curve is called a Simply Connected Domain. Otherwise, it is a multi-connected domain.

h.  A domain with a boundary consisting of closed curves such that each of the curves is outside the other curves, and all within is called an -connected domain.

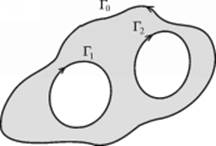
i.  A positive direction on the boundary of connected domain is such that while we move along each of the boundary components, the domain is always on the left. In the illustration, the positive direction on is counterclockwise, while on , it is clockwise.

j.  Set is connected if every two of its inner points can be connected with a continuous curve entirely contained in the set.

k.  An open and connected set is called a domain.