University Mathematics Handbook (2015)

XIV. Partial Differential Equations (PDE)

Chapter 3. Quasi-Linear PDE

 (*)

when , , are of class (see VII.4.3).

Solution or written in its implicit form is called an integral surface.

3.1  General Solution

a.  Surface is an integral surface of (*) if, and only if, in every point on , there holds

b.  An integral surface consists of characteristic curves

Therefore, vectors and are parallel.

c.  To find out all characteristic curves, we solve characteristic equation system

or (**)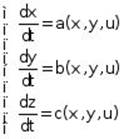

d.  Theorem: If a general solution of (**) is given as the intersection of the two surfaces and , then for every continuous function with partial continuous derivatives, the surface

is an integral surface of (*), for every arbitrary choice of parameters .

3.2  Cauchy Problem

a.  Finding integral surface of PDE (*), passing through characteristic curve is a Cauchy problem.

b.  Existence and Uniqueness Theorem: If, in PDE (*)

1.   in solid .

2.   is a smooth, simple curve (see XII. 1.4).

3.  There holds the transversality criterion

That is, if vectors and are not parallel, then there exists a unique integral surface containing .

c.  If the transversality criterion of b. does not hold, then, when the rank of matrix

is , the Cauchy problem has an infinite number of solutions. When , the Cauchy problem has no solutions.

d.  Lagrange's Method of Solution:

If the general solution of characteristic equation (**) is the line of intersection between surfaces and , and initial condition is also given as the intersection of surfaces , , then, out of these 4 equations, we extract and get a relation between and , which is .

Substituting and , and . We get the required solution (see 3.1.d).