AP Physics C Exam

Part IV

Content Review for the AP Physics C Exam

Chapter 4 Kinematics

INTRODUCTION

Kinematics is the study of an object’s motion in terms of its displacement, velocity, and acceleration. Questions such as How far does this object travel? Or, How fast and in what direction does it move? Or, At what rate does its speed change? All properly belong to kinematics. In the next chapter, we will study dynamics, which delves more deeply into why objects move the way they do.

POSITION, DISTANCE, AND DISPLACEMENT

Position is an object’s relation to a coordinate axis system. Distance is a scalar that represents the total amount traveled by an object. Displacement is an object’s change in position. It’s the vector that points from the object’s initial position to its final position, regardless of the path actually taken. Since displacement means change in position, it is generically denoted s, where denotes change in and s means spatial location. (The letter p is not used for position because it’s reserved for another quantity: momentum.) If it’s known that the displacement is horizontal, then it can be called x; if the displacement is vertical, then it’s y. The magnitude of this vector is the net distance traveled and, sometimes, the word displacement refers just to this scalar quantity. Since a distance is being measured, the SI unit for displacement is the meter.

Example 1 Traveling along a single axis, a car starts 10 m from the origin. The car then moves 8 m directly away from the origin and then turns around and moves 12 m back toward the origin. Determine the final position of the car, the distance the car traveled and the displacement of the car.

Solution. The car ends at the 6 m mark, so the final position is 6 m. The car moves a total of 20 m, so the distance traveled is 20 m. The displacement of the car only refers to the car’s final position minus its initial position. Because the car ended 4 m behind where it started its displacement would be –4 m.

Example 2 An infant crawls 5 m east, then 3 m north, then 1 m east. Find the magnitude of the infant’s displacement.

Solution. Although the infant crawled a total distance of 5 + 3 + 1 = 9 m, this is not the displacement, which is merely the net distance traveled.

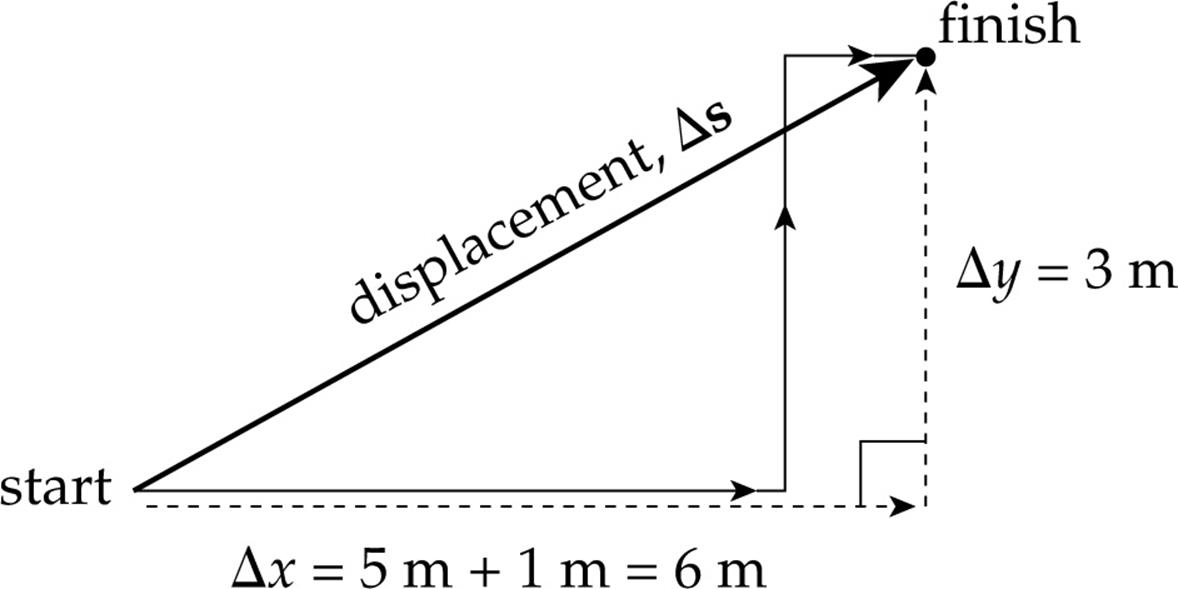
Using the Pythagorean theorem, we can calculate that the magnitude of the displacement is

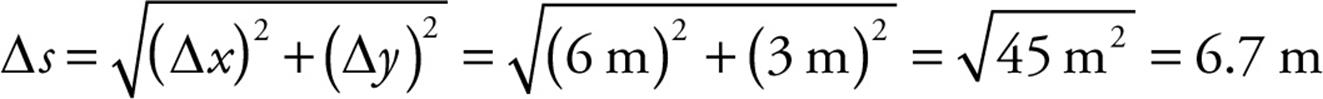
Example 3 In a track-and-field event, an athlete runs exactly once around an oval track, a total distance of 500 m. Find the runner’s displacement for the race.

Solution. If the runner returns to the same position from which she left, then her displacement is zero.

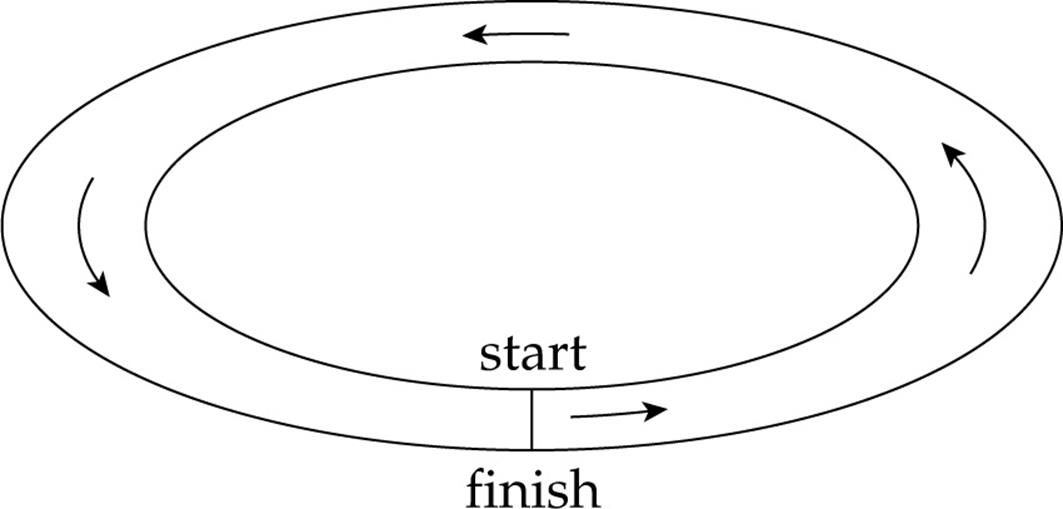
The total distance covered is 500 m, and the displacement is 0.

SPEED AND VELOCITY

When we’re in a moving car, the speedometer tells us how fast we’re going; it gives us our speed. But what does it mean to have a speed of say, 10 m/s? It means that we’re covering a distance of 10 meters every second. By definition, average speed is the ratio of the total distance traveled to the time required to cover that distance:

average speed =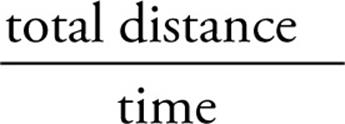

The car’s speedometer doesn’t care in what direction the car is moving (as long as the wheels are moving forward). You could be driving north, south, east, west, whatever; the speedometer would make no distinction. 55 miles per hour, north and 55 miles per hour, east register the same on the speedometer: 55 miles per hour. Speed is a scalar.

However, we will also need to include direction in our descriptions of motion. We just learned about displacement, which takes both distance (net distance) and direction into account. The single concept that embodies both speed and direction is called velocity, and the definition of average velocity is:

average velocity =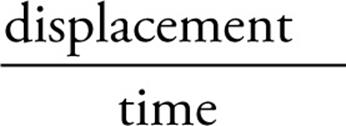

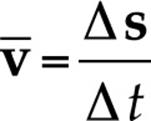
(The bar over the v means average.) Because s is a vector, is also a vector, and because t is a positive scalar, the direction of is the same as the direction of s. The magnitude of the velocity vector is called the object’s speed, and is expressed in units of meters per second (m/s).

Note the distinction between speed and velocity. In everyday language, they’re often used interchangeably. However, in physics, speed and velocity are technical terms whose definitions are not the same. Velocity is speed plus direction. As an important note, the magnitude of the velocity is the speed. However (and this is perhaps a bit unfortunate and can be confusing), the magnitude of the average velocity is not called the average speed. Average speed is defined as the total distance traveled divided by the elapsed time. On the other hand, the magnitude of the average velocity is the displacement divided by the elapsed time.

However, the car’s speedometer is not intended to tell you an average speed over a long period of time: It’s supposed to tell you the current speed at the present moment! For instantaneous speed or velocity, we need calculus. Any shift from an average quantity with deltas in the definition to an instantaneous quantity, especially if the quantity is a rate of change (that is, if Δt is in the denominator), is likely to involve changing “” to “d” and leaving everything else the same, and this is no exception:

v =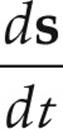

Often, a derivative with respect to time is denoted by a dot above the quantity, so an alternative notation for the equation above is v = ẋ.

Because taking an integral is the inverse of taking a derivative, this definition also implies that displacement is given by the integral of velocity with respect to time:

s = v dt

Example 4 If the infant in Example 2 completes his journey in 20 seconds, find the magnitude of his average velocity.

Solution. Since the displacement is 6.7 m, the magnitude of his average velocity is

= s/t = (6.7 m)/(20 s) = 0.34 m/s

Example 5 Assume that the runner in Example 3 completes the race in 1 minute and 18 seconds. Find her average speed and the magnitude of her average velocity.

Solution. Average speed is total distance divided by elapsed time. Since the length of the track is 500 m, the runner’s average speed was (500 m)/(78 s) = 6.4 m/s. However, since her displacement was zero, her average velocity was zero also: = s/t = (0 m)/(78 s) = 0 m/s.

Example 6 Is it possible to move with constant speed but not constant velocity? Is it possible to move with constant velocity but not constant speed?

Solution. The answer to the first question is yes. For example, if you set your car’s cruise control at 55 miles per hour but turn the steering wheel to follow a curved section of road, then the direction of your velocity changes (which means your velocity is not constant), even though your speed doesn’t change.

The answer to the second question is no. Velocity means speed and direction; if the velocity is constant, then that means both speed and direction are constant. If speed were to change, then the velocity vector’s magnitude would change (by definition), which immediately implies that the vector changes.

Example 7 An object’s position x, in meters, obeys the equation x = sin(t), where t is the time in seconds since the object began moving. How fast is the object moving at seconds?

Solution. Since velocity is the time derivative of position, the velocity is given by v = cos(t). Then plug in the value of t: v() = cos() = 0 m/s.

ACCELERATION

When you step on the gas pedal in your car, the car’s speed increases; step on the brake and the car’s speed decreases. Turn the wheel, and the car’s direction of motion changes. In all of these cases, the velocity changes. To describe this change in velocity, we need a new term:acceleration. In the same way that velocity measures the rate-of-change of an object’s position, acceleration measures the rate-of-change of an object’s velocity. An object’s average acceleration is defined as follows:

average acceleration =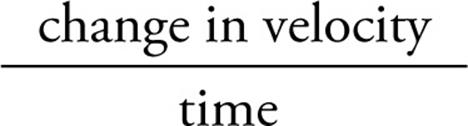

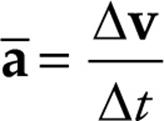
The units of acceleration are meters per second, per second: [a] = m/s². Because v is a vector, ā is also a vector; and because t is a positive scalar, the direction of ā is the same as the direction of v.

Furthermore, if we take an object’s original direction of motion to be positive, then an increase in speed corresponds to a positive acceleration, while a decrease in speed corresponds to a negative acceleration (deceleration).

Note that an object can accelerate even if its speed doesn’t change. (Again, it’s a matter of not allowing the everyday usage of the word accelerate to interfere with its technical, physics usage.) This is because acceleration depends on v, and the velocity vector v changes if (1) speed changes, or (2) direction changes, or (3) both speed and direction change. For instance, a car traveling around a circular racetrack is constantly accelerating even if the car’s speed is constant, because the direction of the car’s velocity vector is constantly changing.

Just as a transition from average velocity to instantaneous velocity changes “” to “d” in an equation, so too does a transition from average acceleration to instantaneous acceleration. Instantaneous acceleration is given by:

a =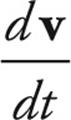

Since velocity is itself the derivative of position, this implies that acceleration is the second derivative of position:

a =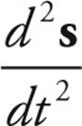

In dot notation, a = = ẍ. The above definition of acceleration also implies that velocity is the integral of acceleration:

v = a dt

The relationships described here can be summarized in the following diagram:

position velocity acceleration
x(t) v(t) a(t)

Example 8 A car is traveling in a straight line along a highway at a constant speed of 80 miles per hour for 10 seconds. Find its acceleration.

Solution. Since the car is traveling at a constant velocity, its acceleration is zero. If there’s no change in velocity, then there’s no acceleration.

Example 9 A car is traveling along a straight highway at a speed of 20 m/s. The driver steps on the gas pedal and, 3 seconds later, the car’s speed is 32 m/s. Find its average acceleration.

Solution. Assuming that the direction of the velocity doesn’t change, it’s simply a matter of dividing the change in velocity, 32 m/s – 20 m/s = 12 m/s, by the time interval during which the change occurred: ā = v/t = (12 m/s) / (3 s) = 4 m/s².

Example 10 Spotting a police car ahead, the driver of the car in the previous example slows from 32 m/s to 20 m/s in 2 seconds. Find the car’s average acceleration.

Solution. Dividing the change in velocity, 20 m/s – 32 m/s = –12 m/s, by the time interval during which the change occurred, 2 s, gives us ā = v/t = (–12 m/s) / (2 s) = –6 m/s². The negative sign here means that the direction of the acceleration is opposite the direction of the velocity, which describes slowing down.

Example 11 The position of an object (measured in meters from the origin, where x = 0) moving along a straight line is given as a function of time t (measured in seconds) by the equation x(t) = 4t² – 6t – 40. Find

(a) its velocity at time t

(b) its acceleration at time t

(d) the object’s velocity and acceleration at the time calculated in (c)

Solution.

(a) The velocity as a function of t is the derivative of the position function:

v(t) = ẋ(t) = 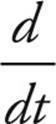(4t² − 6t − 40) = 8t − 6(in m/s)

(b) The acceleration as a function of t is the derivative of the velocity function:

a(t) = (t) = 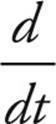(8t − 6) = 8 m/s²

Notice that the acceleration is constant (because it doesn’t depend on t).

4t² – 6t – 40 = 0

2(2t² – 3t – 20) = 0

2(2t + 5)(t – 4) = 0

t = – or 4 seconds

(d) Disregarding the negative value for t, we can say that the object passes through the origin at t = 4 s. At this time, the object’s velocity is

v(4) = v(t)|_t₌₄ = (8t − 6)|_t₌₄ = (8)(4) − 6 = 26 m /s

The object’s acceleration is a constant 8 m/s² throughout its motion, so, in particular, at t = 4 s, the acceleration is 8 m/s².

Example 12 An object is moving along the x-axis with an acceleration given by the function, a(t) = (4t + 7) m/s². At time t₀ = 0, the object is at x = 6 m, and it is moving at 2 m/s. How fast will the object be traveling at time t = 4 s? Where will the object be at time t = 4 s?

Solution. By integrating the acceleration with respect to time, we find the velocity as a function of time.

v(t) = a(t)dt = (4t + 7)dt = 2t² + 7t + c

We determine the value of c, the constant of integration, by using the given initial velocity, v(0) = 2 m/s.

v(0) = 2 (2t² + 7t + c)|_t₌₀ = 2 c = 2

(c is just the initial velocity, v₀). So the velocity function is given by: v(t) = 2t²+ 7t + 2 (in m/s). Therefore, we can evaluate the function at t = 4 s and determine the velocity at that moment of time.

v(4) = (2t² + 7t + 2)|_t _{= 4} (2(4)² + 7(4) + 2) = 62

Integrating this velocity function with respect to time will give us the position function.

x(t) = v(t)dt = (2t² + 7t + 2)dt = t³ + t² + 2t + c₁

Again we determine the constant of integration, c₁, by using the given initial position, x(0) = 6 m.

(c₁, is just the initial position, x₀). So the position function is given by:

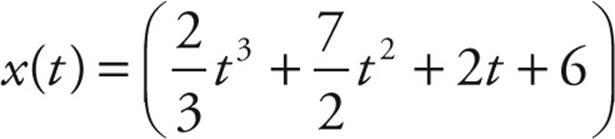in meters

Therefore, we can evaluate the function at t = 4 s and determine the position at that moment of time.

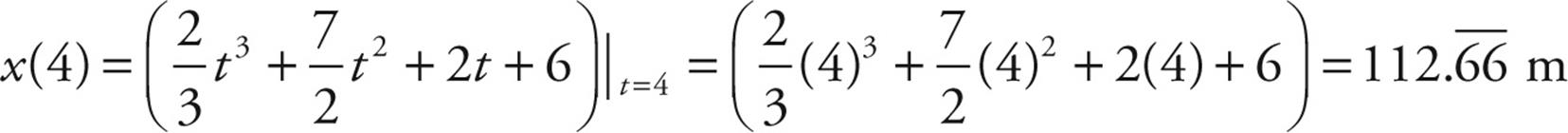
UNIFORMLY ACCELERATED MOTION AND THE BIG FIVE

The simplest type of motion to analyze is motion in which the acceleration is constant (possibly equal to zero). Although true uniform acceleration is rarely achieved in the real world, many common motions are governed by approximately constant acceleration and, in these cases, the kinematics of uniformly accelerated motion provide a pretty good description of what’s happening. Notice that if the acceleration is constant, then taking an average yields nothing new, so ā = a.

Another restriction that will make our analysis easier is to consider only motion that takes place along a straight line. In these cases, there are only two possible directions of motion. One is positive, and the opposite direction is negative. Most of the quantities we’ve been dealing with—displacement, velocity, and acceleration—are vectors, which means that they include both a magnitude and a direction. With straight-line motion, direction can be specified simply by attaching a + or – sign to the magnitude of the quantity. Therefore, although we will often abandon the use of bold letters to denote the vector quantities of displacement, velocity, and acceleration, the fact that these quantities include direction will still be indicated by a positive or negative sign.

Let’s review the quantities we’ve seen so far. The fundamental quantities are displacement (x), velocity (v), and acceleration (a). Acceleration is a change in velocity, from an initial velocity (v_i or v₀) to a final velocity (v_f or simply v—with no subscript). And, finally, the motion takes place during some elapsed time interval, t. Also, if we agree to start our clocks at t₀ = 0 then t = t – 0 = t. We will use t = t to keep the notation cleaner and to match the AP equation sheet. Therefore, we have five kinematics quantities: x, v₀, v, a, and t.

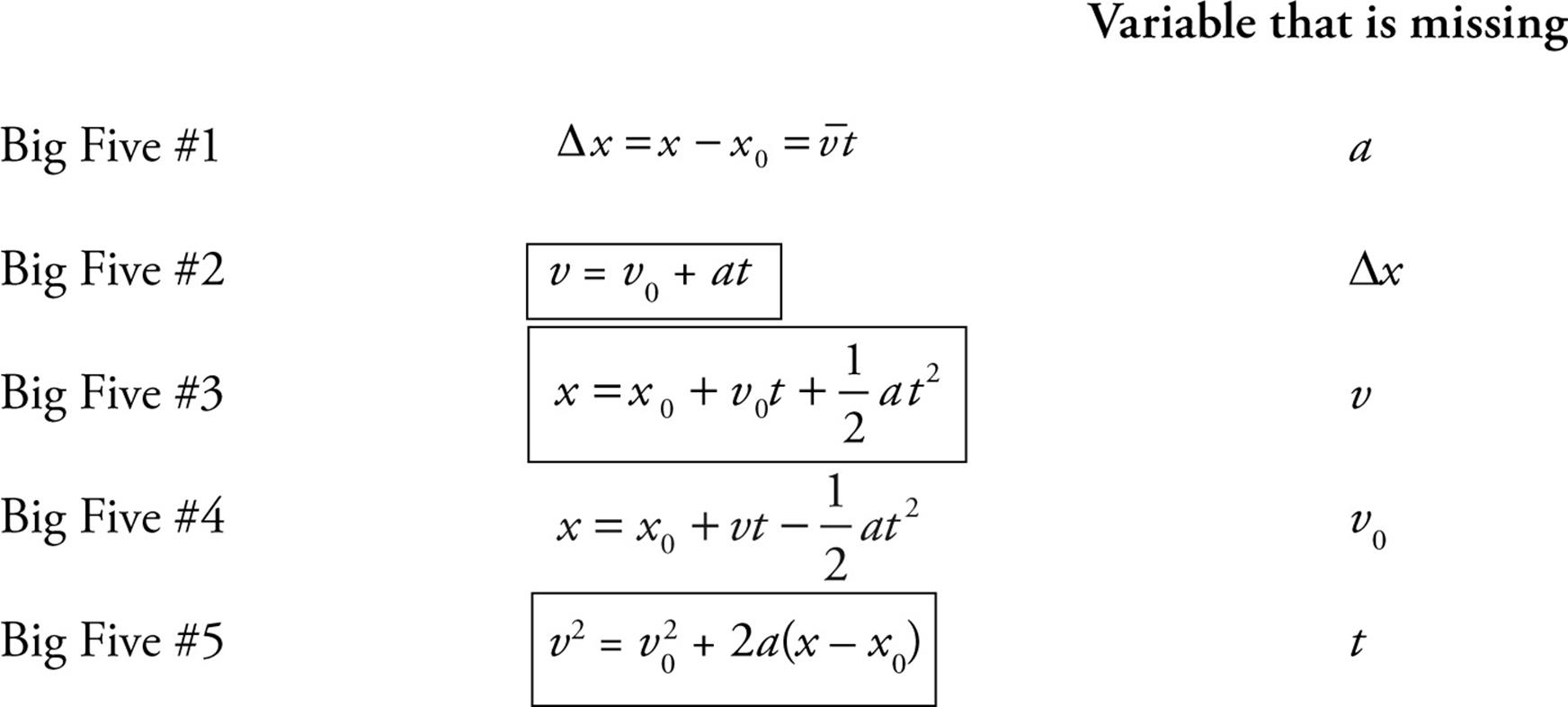
These five quantities are related by a group of five equations that we call the Big Five. They work in cases where acceleration is uniform, which are the cases we’re considering.

It is best to memorize
these equations, as
they are needed for the
multiple-choice section
of the exam, but you are
only allowed to use the
AP equations sheet for the
free-response section.

The change in the position of an object is the displacement: x = x – x₀. Equations #2, #3, and #5 are given on the Advanced Placement Physics C Equations Sheet. They are written here exactly as they will appear on the sheet, which is why we are using x rather than s for the displacement. Throughout this book, equations from the sheet will be enclosed in a box. Because the acceleration is constant, the average velocity is 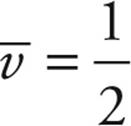(v₀ + v).

Each of the Big Five equations is missing one of the five kinematic quantities. The way you decide which equation to use when solving a problem is to determine which of the kinematic quantities is missing from the problem—that is, which quantity is neither given nor asked for—and then use the equation that doesn’t contain that variable. A good strategy is to make a list of your “knowns” and your “unknowns.” For example, if the problem never mentions the final velocity—v is neither given nor asked for—the equation that will work is the one that’s missing v. That’s Big Five #3.

Big Five #1 and #2 are simply the definitions of and ā written in forms that don’t involve fractions. The other Big Five equations can be derived from these two definitions and the equation 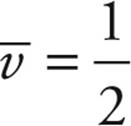(v₀ + v), using a bit of algebra.

Example 13 An object with an initial velocity of 4 m/s moves along a straight axis under constant acceleration. Three seconds later, its velocity is 14 m/s. How far did it travel during this time?

Solution. We’re given v₀, t, and v, and we’re asked for x. So a is missing; it isn’t given and it isn’t asked for, and we use Big Five #1:

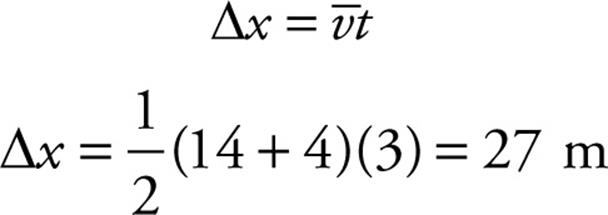
It’s okay to leave off the
units in the middle of the
calculation as long as
you remember to include
them in your final answer.
Leaving units off of your
final answer will cost
you points on the free
-response section of the
AP exam.

Example 14 A car that’s initially traveling at 10 m/s accelerates uniformly for 4 seconds at a rate of 2 m/s², in a straight line. How far does the car travel during this time?

Solution. We’re given v₀, t, and a, and we’re asked for x. So, v is missing; it isn’t given and it isn’t asked for, and we use Big Five #3:

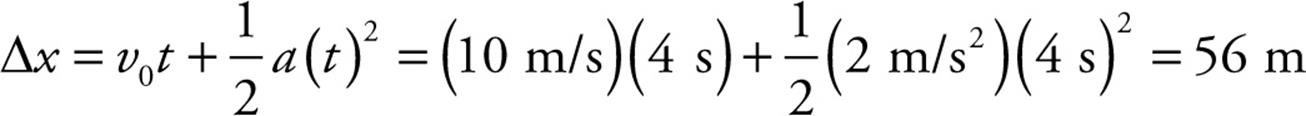
Example 15 A rock is dropped off a cliff that’s 80 m high. If it strikes the ground with an impact velocity of 40 m/s, what acceleration did it experience during its descent?

Solution. If something is dropped, then that means it has no initial velocity: v₀ = 0. So, we’re given v₀, x, and v, and we’re asked for a. Since t is missing, we use Big Five #5, choosing positive as downward:

v² = + 2ax v² = 2ax (since v₀ = 0)

a = 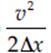= = 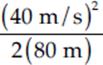10 m/s² downward

Note that since a has the same sign as x, the acceleration vector points in the same direction as the displacement vector. This makes sense here, since the object moves downward and the acceleration it experiences is due to gravity, which also points downward.

KINEMATICS WITH GRAPHS

So far, we have dealt with kinematics problems algebraically, but you should also be able to handle kinematics questions in which information is given graphically. The two most popular graphs in kinematics are position-vs.-time graphs and velocity-vs.-time graphs. For example, consider an object that’s moving along an axis in such a way that its position x as a function of time t is given by the following position-vs.-time graph:

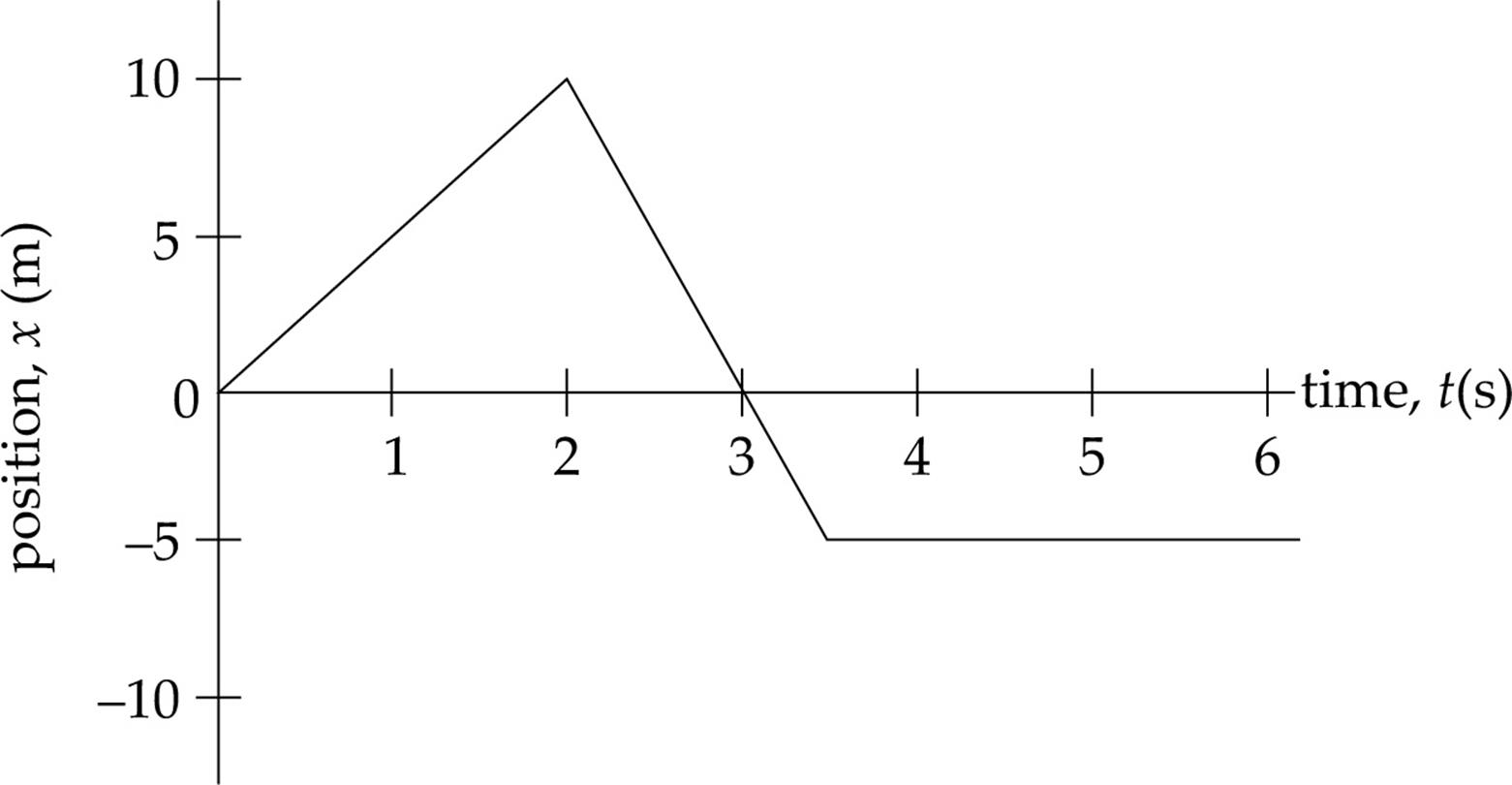
What does this graph tell us? It says that at time t = 0, the object was at position x = 0. Then, in the next two seconds, its position changed from x = 0 to x = 10 m. Then, at time t = 2 s, it reversed direction and headed back toward its starting point, reaching x = 0 at time t = 3 s, and continued, reaching position x = –5 m at time t = 3.5 s. Then the object remained at this position, x = –5 m, at least through time t = 6 s. Notice how economically the graph embodies all this information!

We can also determine the object’s average velocity (and average speed) during particular time intervals. For example, its average velocity from time t = 0 to time t = 2 s is equal to the object’s displacement, 10 – 0 = 10 m, divided by the elapsed time, 2 s:

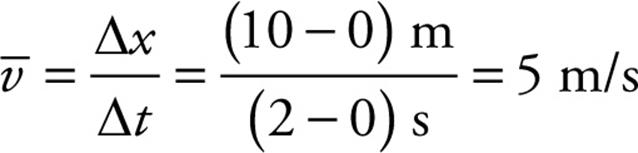
Note, however, that the ratio that defines the average velocity, x/t, also defines the slope of the x-vs.-t graph. Therefore, we know the following important fact:

The slope of a position-vs.-time graph gives the average velocity.

What was the average velocity from time t = 2 s to time t = 3.5 s? The slope of the line segment joining the point (t, x) = (2 s, 10 m) to the point (t, x) = (3.5 s, – 5m) is

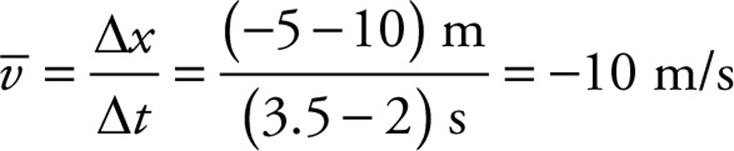
The fact that is negative tells us that the object’s displacement was negative during this time interval; that is, it moved in the negative x direction. The fact that is negative agrees with the observation that the slope of a line that falls to the right is negative. What is the object’s average velocity from time t = 3.5 s to time t = 6 s? Since the line segment from t = 3.5 s to t = 6 s is horizontal, its slope is zero, which implies that the average velocity is zero, but we can also figure this out from looking at the graph, since the object’s position did not change during that time.

Finally, let’s figure out the object’s average velocity and average speed for its entire journey (from t = 0 to t = 6 s). The average velocity is

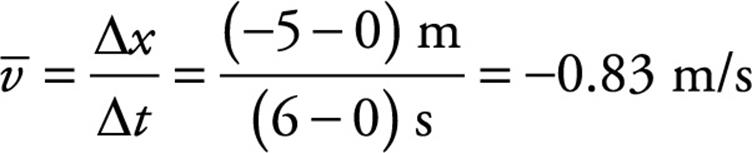
This is the slope of the imagined line segment that joins the point (t, x) = (0 s, 0 m) to the point (t, x) = (6 s, –5 m). The average speed is the total distance traveled by the object divided by the elapsed time. In this case, notice that the object traveled 10 m in the first 2 s, then 15 m (albeit backward) in the next 1.5 s; it covered no additional distance from t = 3.5 s to t = 6 s. Therefore, the total distance traveled by the object is d = 10 + 15 = 25 m, which took 6 s, so

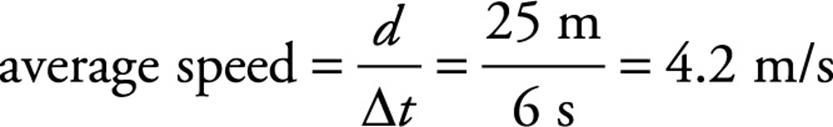
Let’s next consider an object moving along a straight axis in such a way that its velocity, v, as a function of time, t, is given by the following velocity-vs.-time graph:

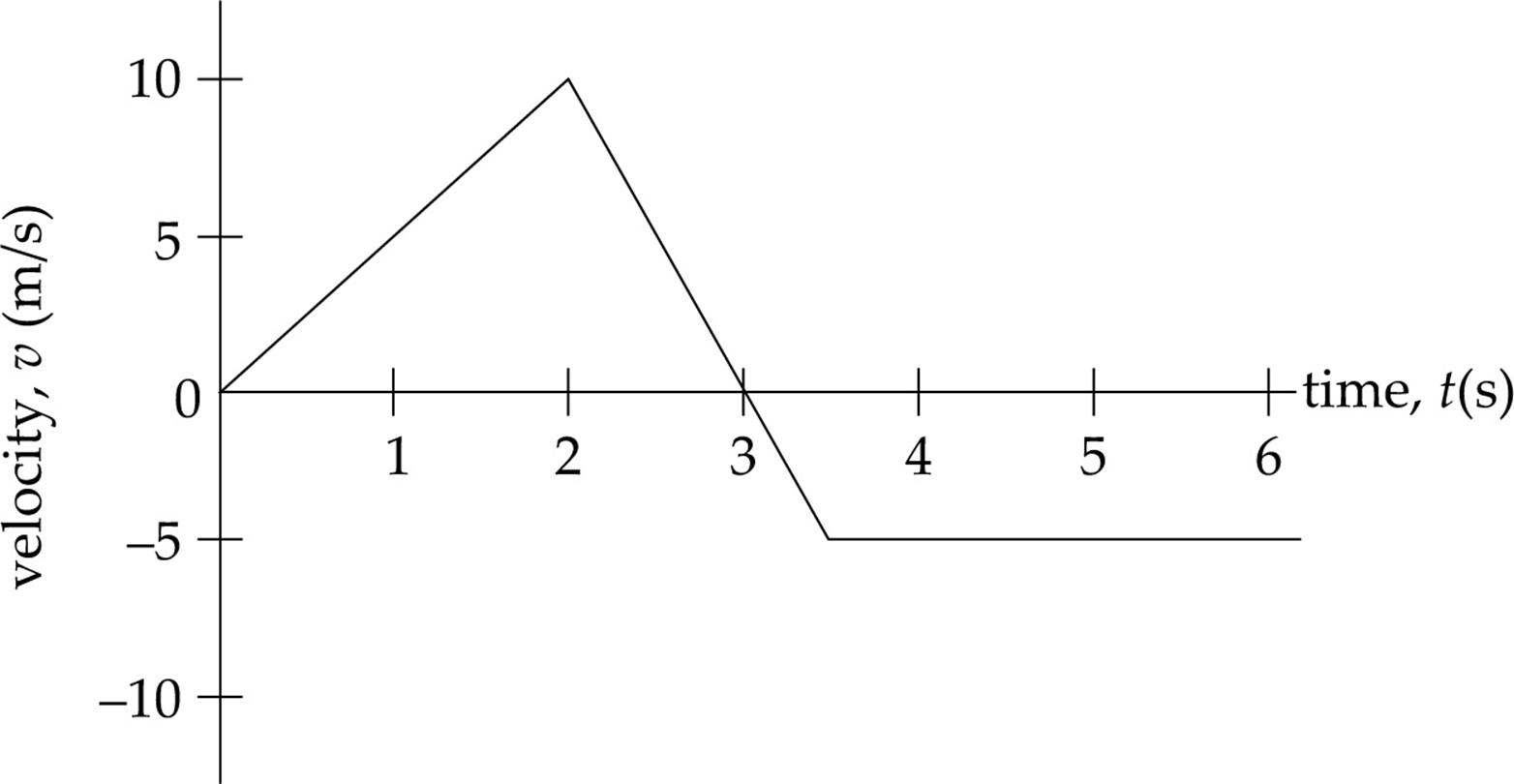
What does this graph tell us? It says that, at time t = 0, the object’s velocity was v = 0. Over the first two seconds, its velocity increased steadily to 10 m/s. At time t = 2 s, the velocity then began to decrease (eventually becoming v = 0, at time t = 3 s). The velocity then became negative after t = 3 s, reaching v = –5 m/s at time t = 3.5 s. From t = 3.5 s on, the velocity remained a steady –5 m/s.

What can we ask about this motion? First, the fact that the velocity changed from t = 0 to t = 2 s tells us that the object accelerated. The acceleration during this time was

Note, however, that the ratio that defines the acceleration, v/t, also defines the slope of the v vs. t graph. Therefore,

The slope of a velocity-vs.-time graph gives the average acceleration.

What was the acceleration from time t = 2 s to time t = 3.5 s? The slope of the line segment joining the point (t, v) = (2 s, 10 m/s) to the point (t, v) = (3.5 s, –5 m/s) is

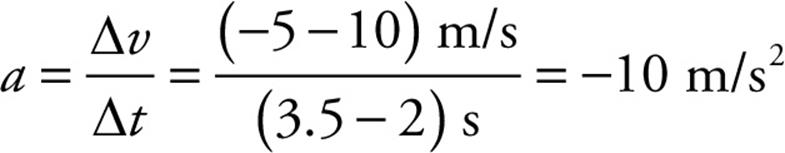
The fact that a is negative tells us that the object’s velocity change was negative during this time interval; that is, the object accelerated in the negative direction. In fact, after time t = 3 s, the velocity became more negative, indicating that the direction of motion was negative at increasing speed. What is the object’s acceleration from time t = 3.5 s to time t = 6 s? Since the line segment from t = 3.5 s to t = 6 s is horizontal, its slope is zero, which implies that the acceleration is zero, but you can also see this from looking at the graph; the object’s velocity did not change during this time interval.

Another question can be asked when a velocity-vs.-time graph is given: How far did the object travel during a particular time interval? For example, let’s figure out the displacement of the object from time t = 4 s to time t = 6 s. During this time interval, the velocity was a constant –5 m/s, so the displacement was x = vt = (–5 m/s)(2 s) = –10 m.

Geometrically, we’ve determined the area between the graph and the horizontal axis. After all, the area of a rectangle is base × height and, for the shaded rectangle shown below, the base is t, and the height is v. So, base × height equals t × v, which is displacement.

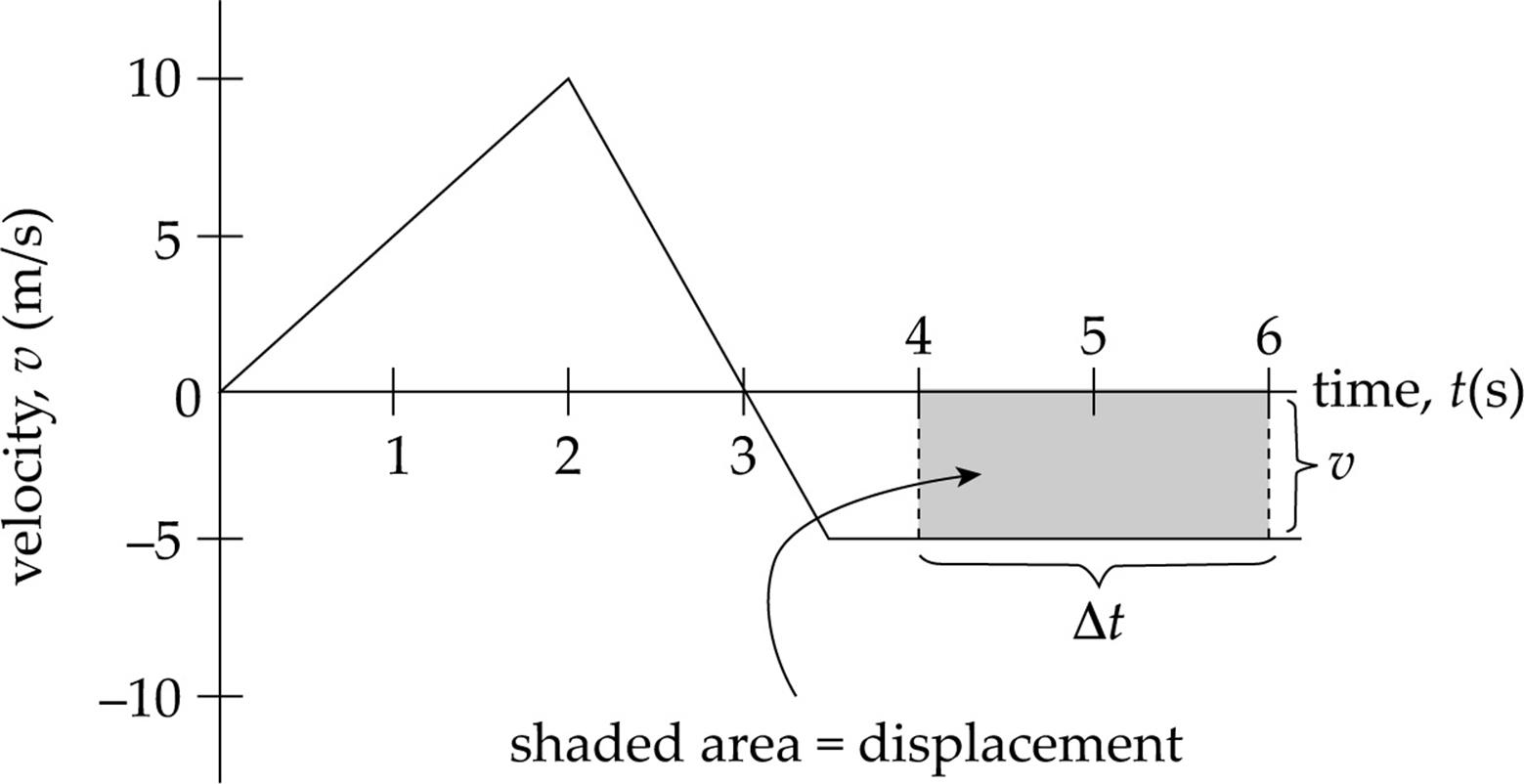
Counting areas above the horizontal axis as positive and areas below the horizontal axis as negative, we can make the following claim:

Given a velocity-vs.-time graph, the area between the graph and the t-axis equals the object’s displacement.

What is the object’s displacement from time t = 0 to t = 3 s? Using the fact that displacement is the area bounded by the velocity graph, we figure out the area of the triangle shown below:

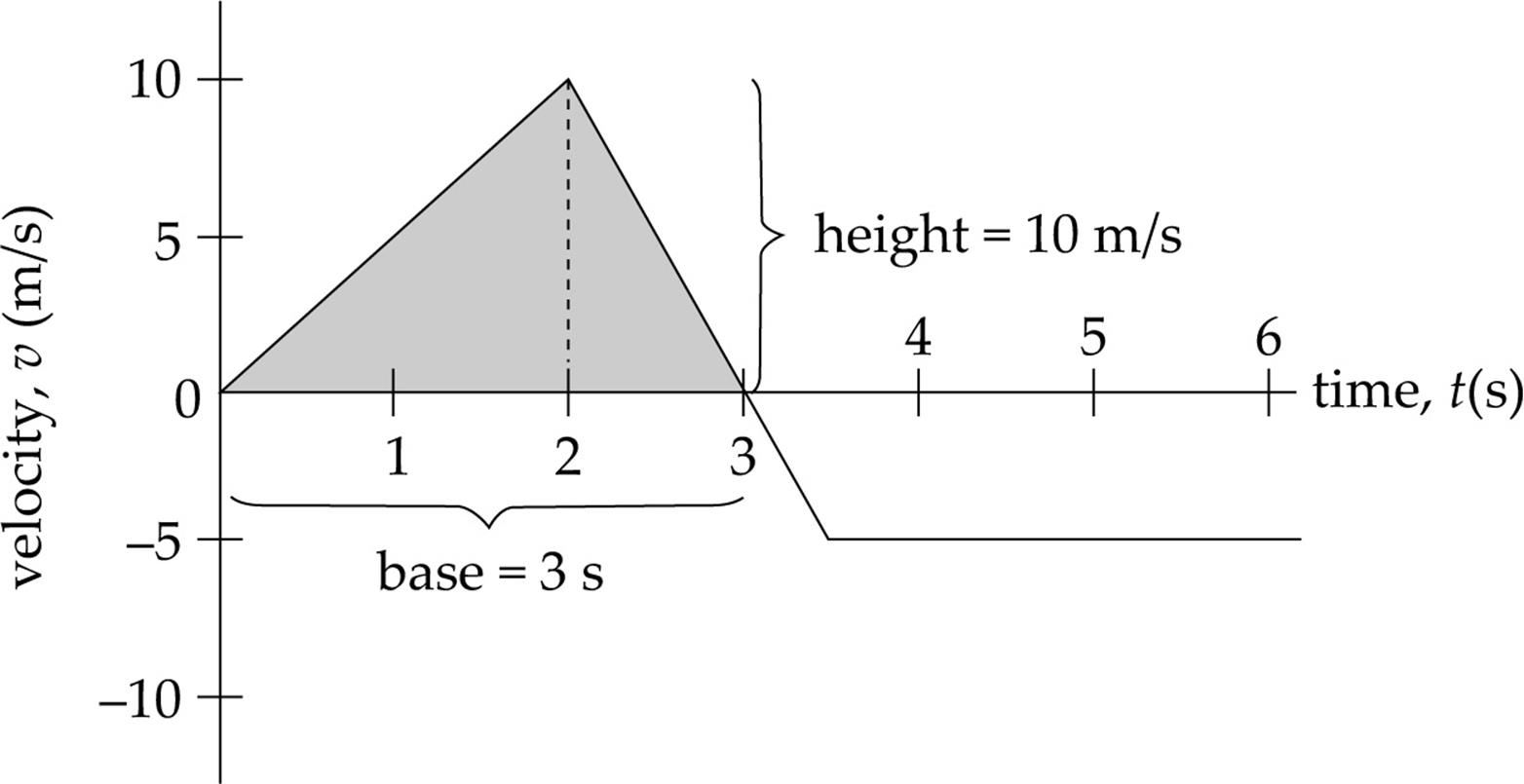
Since the area of a triangle is × base × height, we find that x = (3 s)(10 m/s) = 15 m.

A Note About Calculus

The use of graphs for solving kinematics questions provides a link to some basic definitions in calculus. The slope of a curve is the geometric definition of the derivative of a function. Since the slope of a position-vs.-time graph gives the velocity, the derivative of a position function gives the velocity. That is, given an equation of the form x = x(t) for the position x of an object as a function of time t, the derivative of x(t)—with respect to t—gives the object’s velocity v(t):

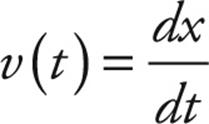
Often, a derivative with respect to time is denoted by a dot above the quantity, so an alternative notation for the equation above is v(t) = ẋ(t).

Next, since the slope of a velocity-vs.-time graph gives the acceleration, the derivative of a velocity function gives the acceleration. That is, given an equation of the form v = v(t) for the velocity v of an object as a function of time t, the derivative of v(t)—with respect to t—gives the object’s acceleration a(t):

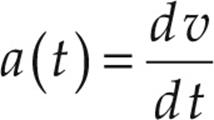
Combining this equation with the previous one, we see that the acceleration is the second derivative of the position:

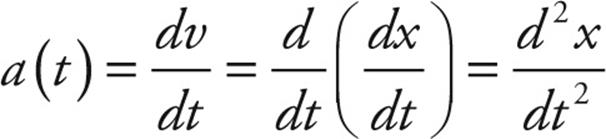
Using the dot notation, these last two equations may be written as a(t) = (t) and a(t) = ẍ(t), respectively.

The signed area bounded by a curve and the horizontal axis is the geometric definition of the definite integral of a function. Since the area bounded by a velocity-vs.-time graph gives the displacement, the definite integral of a velocity function gives the displacement. That is, given the equation v = v(t) for the velocity v of an object as a function of time t, the integral of v(t) from time t = t₁ to time t = t₂ equals the displacement during this time interval:

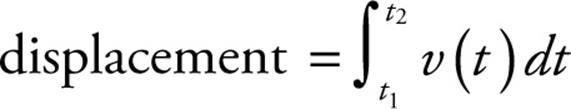
For the velocity-vs.-time graph examined above, the slope of the line segment from (t, v) = (0, 0) to (t, v) = (2, 10) can be described by the equation v(t) = 5t, and the line segment from (t, v) = (2, 10) to (t, v) = (3, 0) can be described by the equation v(t) = –10t + 30 (with t in seconds and vin m/s in both equations). Therefore, the acceleration of the object from time t = 0 to t = 2 s is

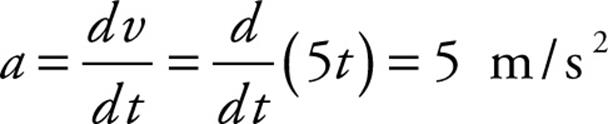
as we found above.

Also, the displacement of the object from time t = 0 to t = 3 s is the value of the integral from t = 0 to t = 3 s, which we can get by adding the integral of v(t) = 5t from t = 0 to t = 2 s to the integral of v(t) = –10t + 30 from t = 2 s to t= 3 s:

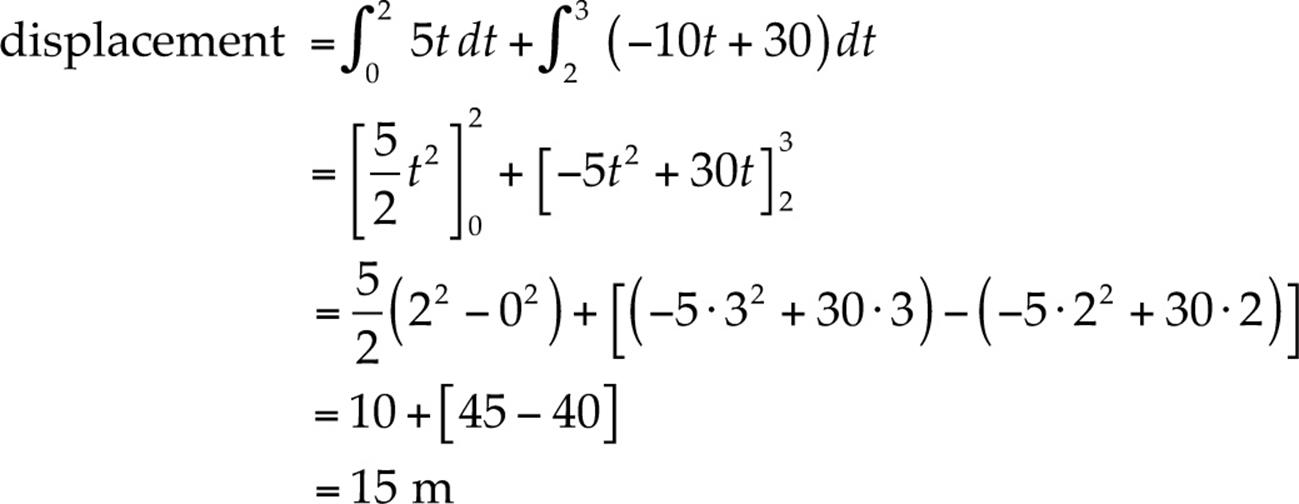
which also agrees with the value computed above.

Example 16 The velocity of an object as a function of time is given by the following graph:

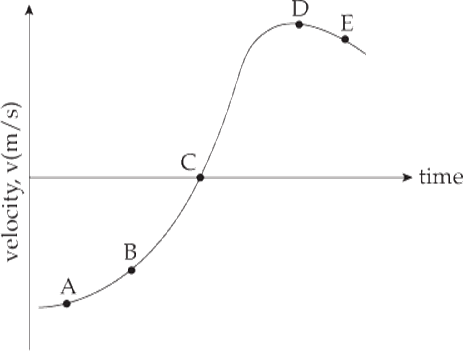
At which point (A, B, C, D, or E) is the magnitude of the acceleration the greatest? How would you answer this same question if the graph shown were a position-vs.-time graph?

Solution. The acceleration is the slope of the velocity-vs.-time graph. Although this graph is not composed of straight lines, the concept of slope still applies; at each point, the slope of the curve is the slope of the tangent line to the curve. The slope is essentially zero at Points A and D (where the curve is flat), small and positive at B, and small and negative at E. The slope at Point C is large and positive, so this is where the object’s acceleration is the greatest.

If the graph shown were a position-vs.-time graph, then the slope would be the velocity. The slope of the given graph starts at zero (around Point A), slowly increases to a small positive value at B, continues to slowly increase to a large positive value at C, then, at around Point D, this large positive slope decreases quickly to zero. Of the points designated on the graph, Point D is the location of the greatest slope change, which means that this is the point of the greatest velocity change. Therefore, this is the point at which the magnitude of the acceleration is greatest.

Average vs. Instantaneous Quantities

We have a variety of methods to determine the velocity and the acceleration of an object. We also need to distinguish between average quantities and instantaneous quantities. Average velocity is the displacement over some time interval, while instantaneous velocity is how fast the object is traveling at a specific instant of time. The speedometer on a car gives us the instantaneous speed (it does not indicate the direction, so it does not indicate the instantaneous velocity). Typically, it is easiest to solve for average quantities using the definitions mentioned before. It is easiest to solve for instantaneous quantities by using one of the Big Five equations, or taking the slope of a given graph or derivative of a given function. Make sure you carefully read the question and understand whether they are asking for an average quantity or an instantaneous quantity.

FREE FALL

The simplest real-life example of motion under pretty constant acceleration is the motion of objects in Earth’s gravitational field, near the surface of Earth and ignoring any effects due to the air (mainly air resistance). Under these conditions, an object can fall freely, that is, it can fall experiencing only acceleration due to gravity. Near the surface of Earth, the gravitational acceleration has a constant magnitude of about 9.8 m/s²; this quantity is denoted g (for gravitational acceleration). On the AP Physics C Exam, you may use g = 10 m/s² as a simple approximation tog = 9.8 m/s². This is particularly helpful because, as we mentioned earlier, you will not be permitted to use a calculator on the multiple-choice section. In this book, we will always use g = 10 m/s². And, of course, the gravitational acceleration vector, g, points downward.

Since the acceleration is constant, we can use the Big Five with a replaced by +g or –g. We will use y for displacement rather than s or x because the motion is vertical. To decide which of these two values to use for a, make a decision at the beginning of your calculations whether to call “down” the positive direction or the negative direction. If you call “down” the positive direction, then a = +g. If you call “down” the negative direction, then a = –g. We will always assume up is the positive direction unless all of the motion is downward.

In each of the following examples, we’ll ignore effects due to the air.

Example 17 A rock is dropped from an 80-meter cliff. How long does it take to reach the ground?

Solution. Since all of the rock’s motion is down, we call down the positive direction, so a = +g. We’re given v₀, y, and a, and we are asked for t. So v is missing; it isn’t given and it isn’t asked for, and we use Big Five #3:

y = y₀ + v₀t + gt² y = g t² (since y₀ = 0, and v₀ = 0)

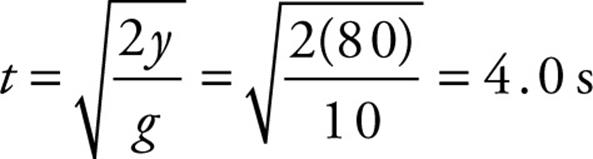
Example 18 A baseball is thrown straight upward with an initial speed of 20 m/s. How high will it go?

Solution. Since the ball travels upward, call up the positive direction. Therefore, down is the negative direction, so a = –g. The ball’s velocity drops to zero at the instant the ball reaches its highest point, so we’re given a, v₀, and v, and asked for y. Since t is missing, we use Big Five #5:

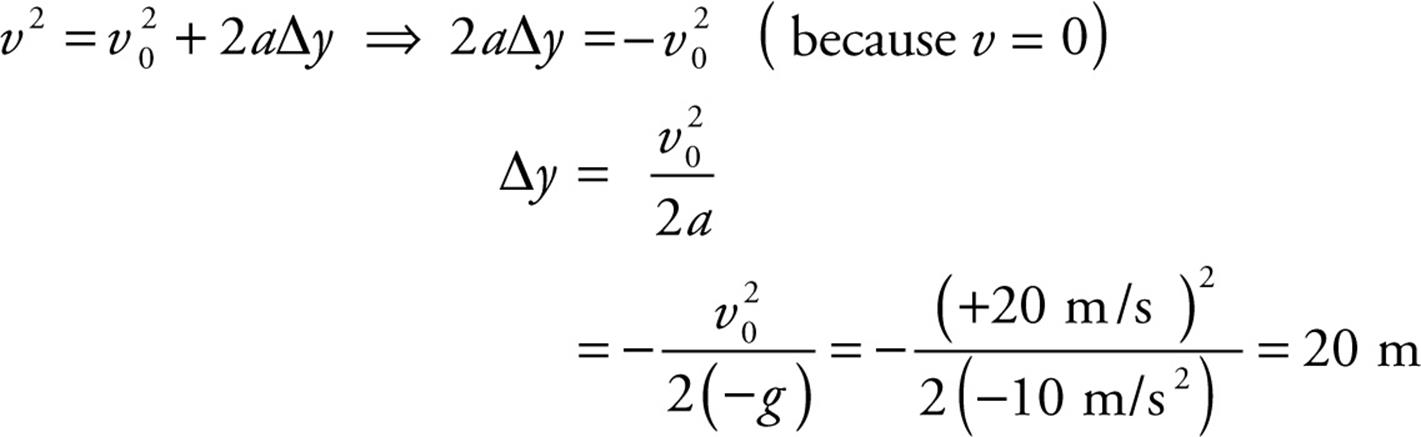
Example 19 One second after being thrown straight down, an object is falling with a speed of 20 m/s. How fast will it be falling 2 seconds after it was traveling 20 m/s?

Solution. Because all the motion is downward, call down the positive direction, so a = +g and v₀ = +20 m/s. We’re given v₀, a, and t, and asked for v. Since y is missing, we use Big Five #2:

v = v₀ + at = (+20 m/s) + (+10 m/s²)(2 s) = 40 m/s

Example 20 If an object is thrown straight upward with an initial speed of 8 m/s and takes 3 seconds to strike the ground, from what height was the object thrown?

Solution. The figure below shows the path of the ball. We will use up as positive because not all the motion is downward. Therefore a = –g. We’re given a, v₀, and t, and we need to find y. Since v is missing, we use Big Five #3:

PROJECTILE MOTION

In general, an object that moves near the surface of Earth will not follow a straight-line path (for example, a baseball hit by a bat, a golf ball struck by a club, or a tennis ball hit from the baseline). If we launch an object at an angle other than straight upward and consider only the effect of acceleration due to gravity, then the object will travel along a parabolic trajectory.

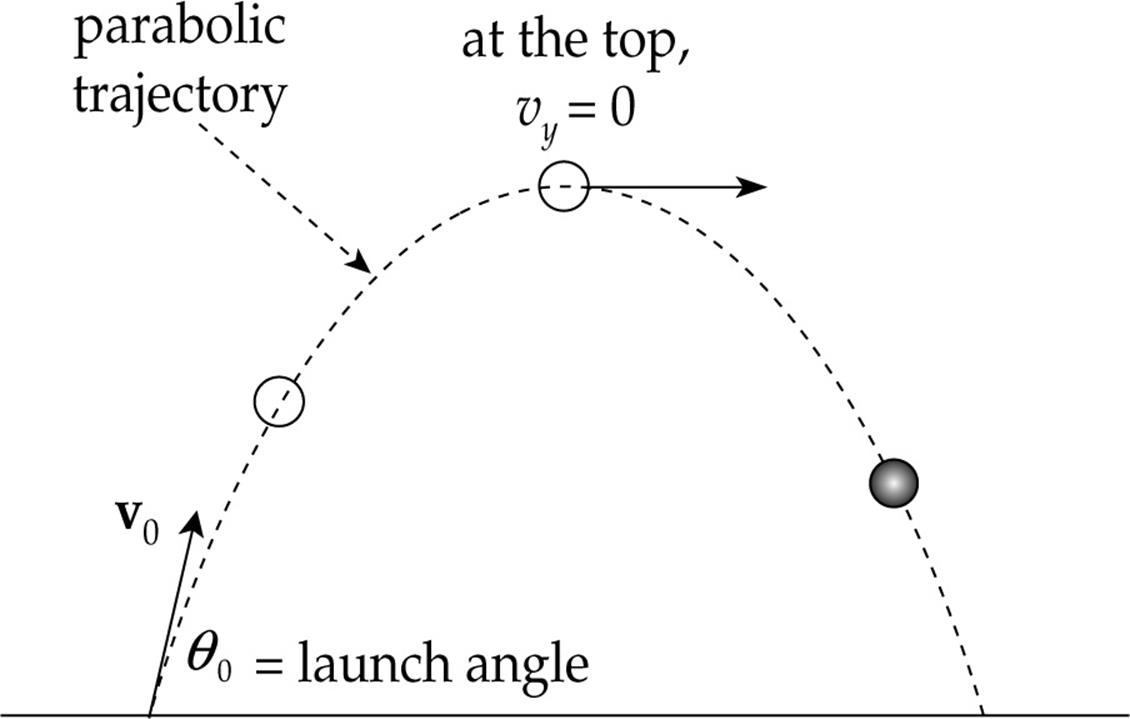
To simplify the analysis of parabolic motion, we analyze the horizontal and vertical motions separately, using the Big Five. This is the key to doing projectile motion problems. Calling down the negative direction, we have

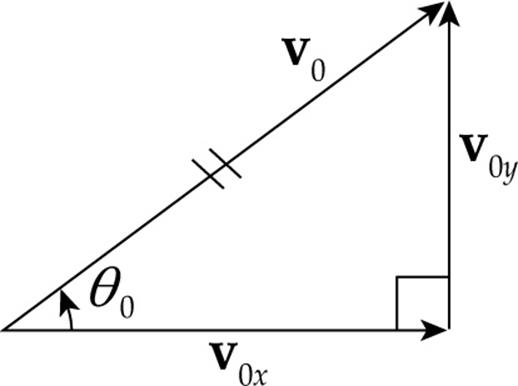
The quantity v_0x, which is the horizontal (or x) component of the initial velocity, is equal to v₀ cos θ₀, where θ₀ is the launch angle, the angle that the initial velocity vector, v₀, makes with the horizontal. Similarly, the quantity v_0y, the vertical (or y) component of the initial velocity, is equal to v₀ sin θ₀.

Example 21 An object is thrown horizontally off a cliff with an initial speed of 10 m/s. How far will it drop in 4 seconds assuming it does not hit the ground first?

Solution. The first step is to decide whether this is a horizontal question or a vertical question, since you must consider these motions separately. The question, How far will it drop?, is a vertical question, so the set of equations we will consider are those listed above under vertical motion. Next, “How far will it drop?” implies that we will use the first of the vertical-motion equations, the one that gives vertical displacement, y.

Now, since the object is thrown horizontally, there is no vertical component to its initial velocity vector v₀; that is, v_0y = 0. Therefore,

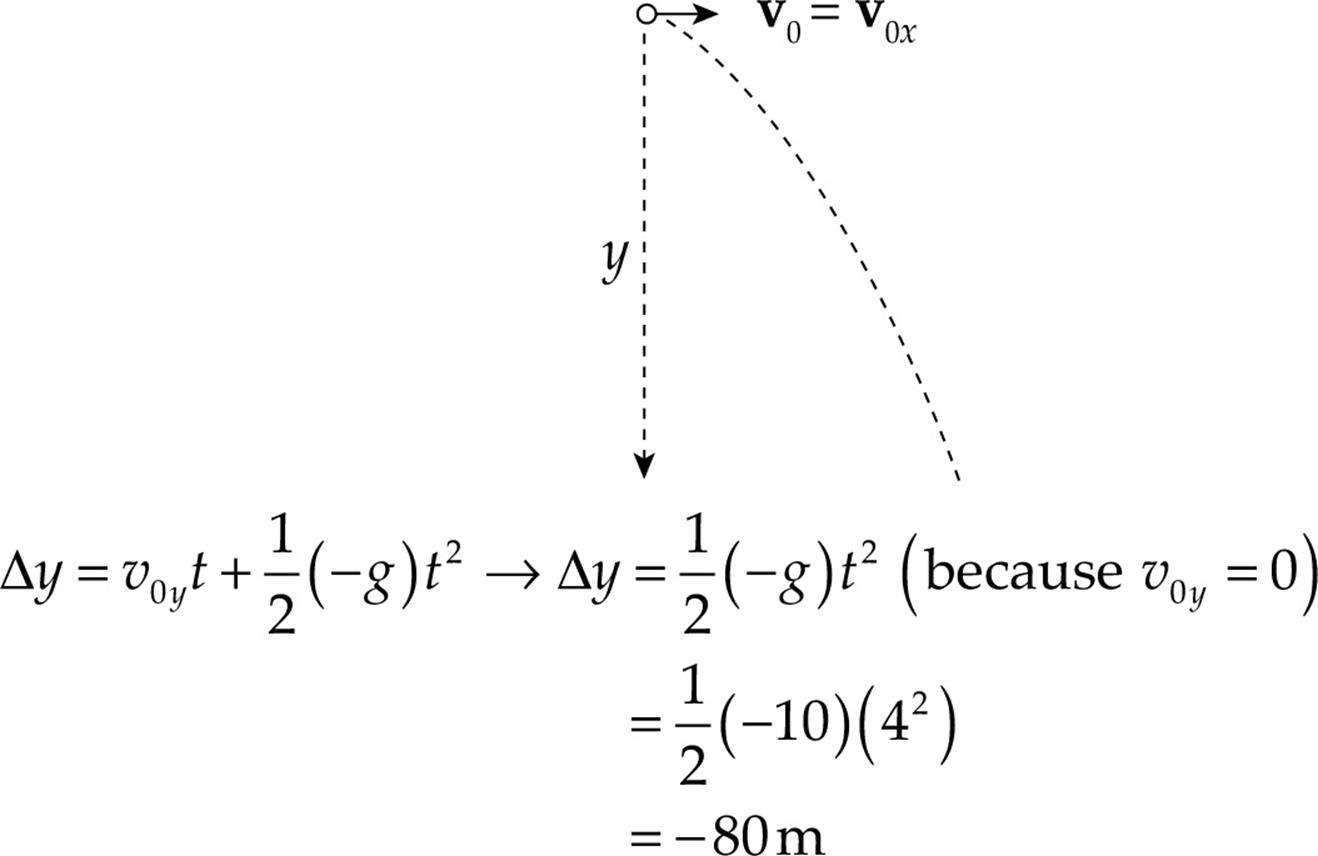
The fact that y is negative means that the displacement is down. Also, notice that the information given about v_0x is irrelevant to the qustion.

Example 22 From a height of 100 m, a ball is thrown horizontally with an initial speed of 15 m/s. How far does it travel horizontally in the first 2 seconds?

Solution. The question, “How far does it travel horizontally?” immediately tells us that we should use the first of the horizontal-motion equations:

x = v_0xt = (15 m/s)(2 s) = 30 m

The information that the initial vertical position is 100 m above the ground is irrelevant (except for the fact that it’s high enough that the ball doesn’t strike the ground before the two seconds have elapsed).

Example 23 A projectile is traveling in a parabolic path for a total of 6 seconds. How does its horizontal velocity 1 s after launch compare to its horizontal velocity 4 s after launch?

Solution. The only acceleration experienced by the projectile is due to gravity, which is purely vertical, so that there is no horizontal acceleration. If there’s no horizontal acceleration, then the horizontal velocity cannot change during flight, and the projectile’s horizontal velocity 1 s after it’s launched is the same as its horizontal velocity 3 s later.

Example 24 An object is projected upward with a 30° launch angle and an initial speed of 40 m/s. How long will it take for the object to reach the top of its trajectory? How high is this?

Solution. When the projectile reaches the top of its trajectory, its velocity vector is momentarily horizontal; that is, v_y = 0. Using the vertical-motion equation for v_y, we can set it equal to 0 and solve for t:

At this time, the projectile’s vertical displacement is

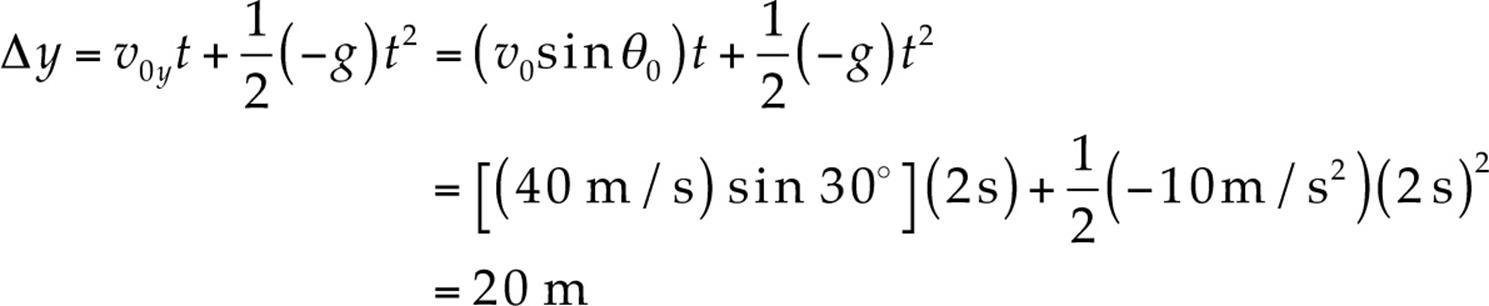
Example 25 An object is projected upward with a 30° launch angle and an initial speed of 60 m/s. For how many seconds will it be in the air? How far will it travel horizontally before returning to its original height?

Solution. The total time the object spends in the air is equal to twice the time required to reach the top of the trajectory (because the parabola is symmetrical). So, as we did in the previous example, we find the time required to reach the top by setting v_y equal to 0, and now double that amount of time:

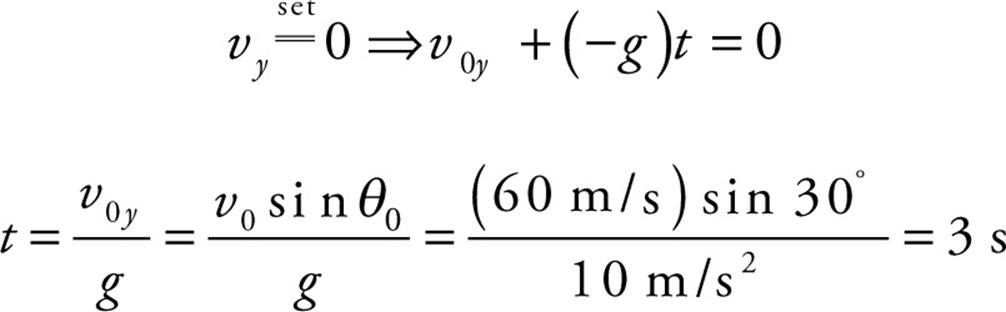
Therefore, the total flight time (that is, up and down) is T = 2t = 2 × (3 s) = 6 s.

Now, using the first horizontal-motion equation, we can calculate the horizontal displacement after 6 seconds:

x = v_0x T = (v₀ cos θ₀)T = [(60 m/s) cos 30°](6 s) = 310 m

By the way, the full horizontal displacement of a projectile to the same height is called the projectile’s range.

A Note About Notation

We are trying to be as consistent as possible with the test by using equations identical to those on the AP Equations Sheet that you will be given to use during the free-response section of the exam. When the motion is vertical we use y instead of x, and occasionally use s to indicate when the motion is in two dimensions. It is important that you judge which variable best represents the values you are given and those you need to solve for.

CHAPTER 4 REVIEW QUESTIONS

The answers and explanations can be found in Chapter 16.

Section I: Multiple Choice

1. An object that’s moving with constant speed travels once around a circular path. Which of the following is/are true concerning this motion?

I. The displacement is zero.

II. The average speed is zero.

III. The acceleration is zero.

(A) I only

(B) I and II only

(D) III only

(E) II and III only

2. At time t = t₁, an object’s velocity is given by the vector v₁ shown below:

A short time later, at t = t₂, the object’s velocity is the vector v₂:

If v₂ = v₁, which one of the following vectors best illustrates the object’s average acceleration between t = t₁ and t = t₂?

(A)

(B)

(C)

(D)

(E)

3. Which of the following is/are true?

I. If an object’s acceleration is constant, then it must move in a straight line.

II. If an object’s acceleration is zero, then its speed must remain constant.

III. If an object’s speed remains constant, then its acceleration must be zero.

(A) I and II only

(B) I and III only

(D) III only

(E) II and III only

4. A baseball is thrown straight upward. What is the ball’s acceleration at its highest point?

(A) 0

(B) g, downward

(D) g, upward

(E) g, upward

5. How long would it take a car, starting from rest and accelerating uniformly in a straight line at 5 m/s², to cover a distance of 200 m?

(A) 9.0 s

(B) 10.5 s

(D) 15.5 s

(E) 20.0 s

6. A rock is dropped off a cliff and strikes the ground with an impact speed of 30 m/s. How high was the cliff?

(A) 15 m

(B) 20 m

(D) 45 m

(E) 60 m

7. A stone is thrown horizontally with an initial speed of 10 m/s from a bridge. If air resistance could be ignored, how long would it take the stone to strike the water 80 m below the bridge?

(A) 1 s

(B) 2 s

(D) 6 s

(E) 8 s

8. A soccer ball, at rest on the ground, is kicked with an initial velocity of 10 m/s at a launch angle of 30°. Calculate its total flight time, assuming that air resistance is negligible.

(A) 0.5 s

(B) 1 s

(D) 2 s

(E) 4 s

9. A stone is thrown horizontally with an initial speed of 30 m/s from a bridge. Find the stone’s total speed when it enters the water 4 seconds later. (Ignore air resistance.)

(A) 30 m/s

(B) 40 m/s

(D) 60 m/s

(E) 70 m/s

10. Which one of the following statements is true concerning the motion of an ideal projectile launched at an angle of 45° to the horizontal?

(A) The acceleration vector points opposite to the velocity vector on the way up and in the same direction as the velocity vector on the way down.

(B) The speed at the top of the trajectory is zero.

(D) The horizontal speed decreases on the way up and increases on the way down.

(E) The vertical speed decreases on the way up and increases on the way down.

11. The position of an object moving in a straight line is given by x = (7 + 10t – 6t³) m, where t is in seconds. What is the object’s velocity at 4 seconds?

(A) –8 m/s

(B) –62 m/s

(D) –278 m/s

(E) none of the above

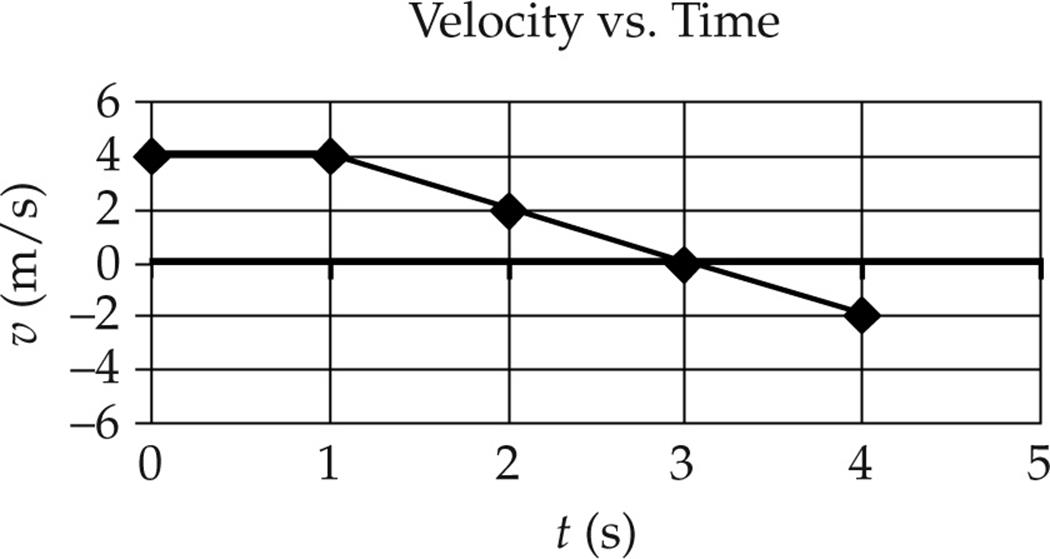
12. The velocity of an object moving in a straight line is graphed above. If x = 3.0 m at t = 0 s, what is the position of the particle at t = 3.0 s?

(A) 6 m

(B) 10 m

(D) 11 m

(E) –5 m

Section II: Free Response

1. This question concerns the motion of a car on a straight track; the car’s velocity as a function of time is plotted below.

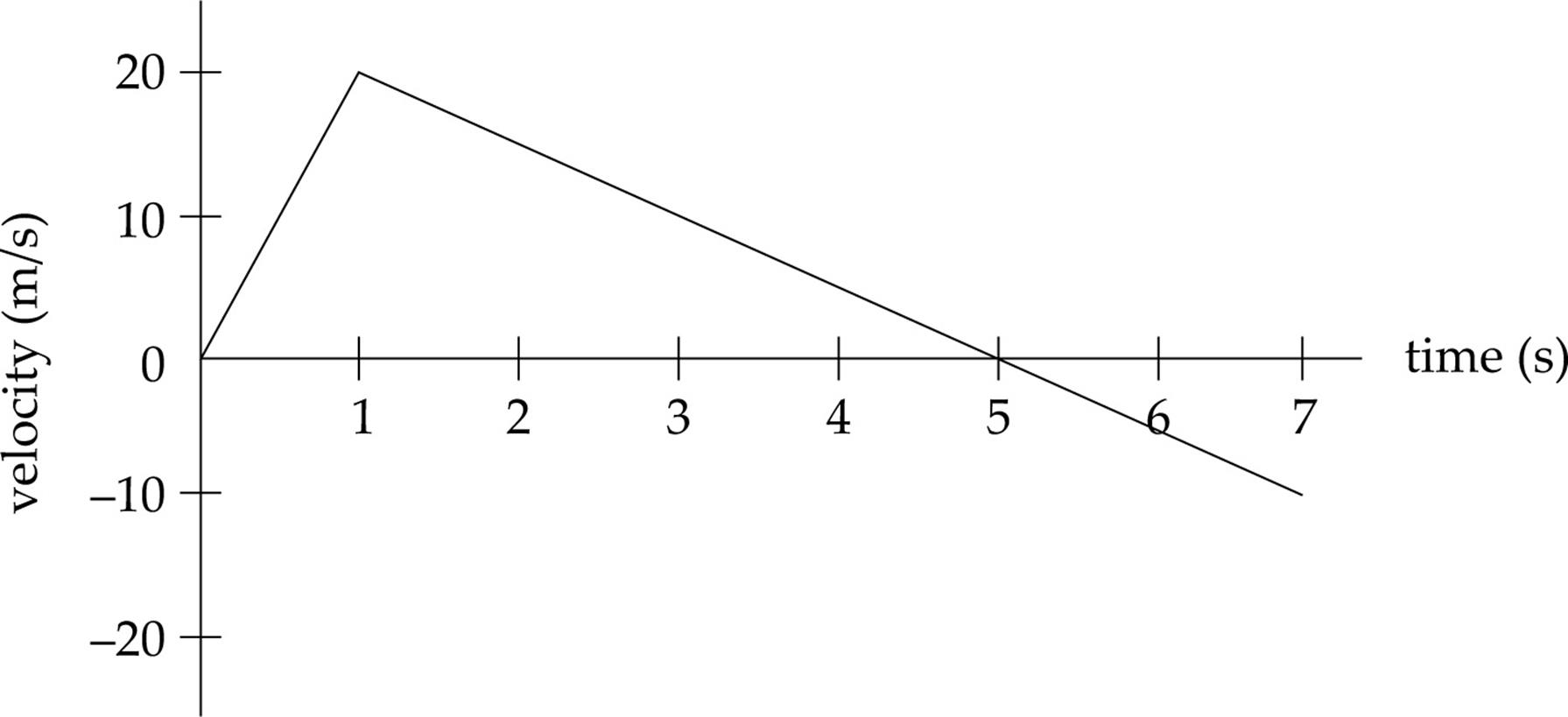
(a) Describe what happened to the car at time t = 1 s.

(b) How does the car’s average velocity between time t = 0 and t = 1 s compare to its average velocity between times t = 1 s and t = 5 s?

(d) Plot the car’s acceleration during this interval as a function of time.

(e) Plot the object’s position during this interval as a function of time. Assume that the car begins at s = 0.

2. Consider a projectile moving in a parabolic trajectory under constant gravitational acceleration. Its initial velocity has magnitude v₀, and its launch angle (with the horizontal) is θ₀. Solve the following in terms of given quantities and the acceleration of gravity, g.

(a) Calculate the maximum height, H, of the projectile.

(b) Calculate the (horizontal) range, R, of the projectile.

(d) If 0 < h < H, compute the time that elapses between passing through the horizontal line of height h in both directions (ascending and descending); that is, compute the time required for the projectile to pass through the two points shown in this figure:

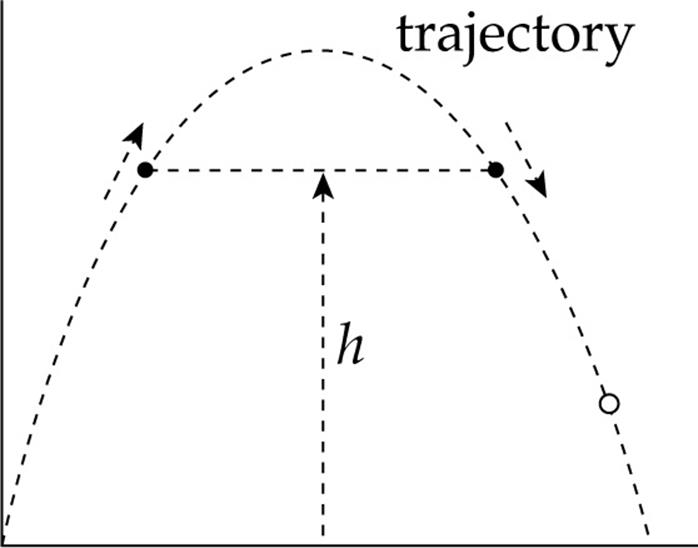
3. A cannonball is shot with an initial speed of 50 m/s at a launch angle of 40° toward a castle wall 220 m away. The height of the wall is 30 m. Assume that effects due to the air are negligible. (For this problem, use g = 9.8 m/s².)

(a) How long will it take the cannonball to reach the vertical plane of the wall?

(b) Will the cannonball strike the wall? If the cannonball strikes the wall, how far below the top of the wall does it strike? If the cannonball does not strike the wall, how much does it clear the wall by?

4. A particle moves along a straight axis in such a way that its acceleration at time t is given by the equation a(t) = 6t (m/s²). If the particle’s initial velocity is 2 m/s and its initial position is x = 4 m, determine

(a) The time at which the particle’s velocity is 14 m/s

(b) The particle’s position at time t = 3 s.

Summary

Definitions

Position refers to where an object is relative to a coordinate axes system.
Distance refers to the total measure of the ground traveled by an object.
Displacement is how far an object is from where it started. It can be represented as the final position minus the initial position: Δs = s_f – s_i.

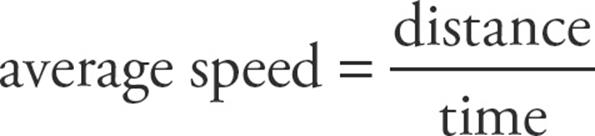
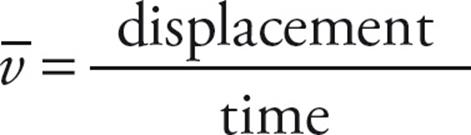
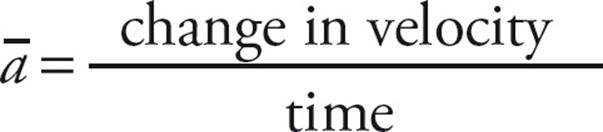
Constant Acceleration Equations

The Big 5 acceleration equations are

x = x − x₀ = t

v = v₀ + at

x = x₀ + v₀t + at²

x = x₀ + vt − at²

v² = v²₀ + 2a(x − x₀)

Graphs

The slope of a position-vs.-time graph is the average velocity.
The area between the t-axis and the velocity function is the displacement.
The slope of a velocity-vs.-time graph is the average acceleration.

Motion Functions

The derivate of x(t) is the velocity.
The integral of v(t) is the displacement.
The derivative of v(t) is the acceleration.

Free Fall and Projectiles

The acceleration due to gravity, g, is a constant 9.8 m/s² downward, for all objects close to the surface of Earth. Note that the test directions state that to simplify calculations you may use 10 m/s² in all problems.
Remember to analyze the vertical (constant acceleration) and horizontal (constant velocity) motions separately. You can use the constant acceleration equations with a replaced by g and x replaced by y to indicate the acceleration is in the vertical direction. The motion in the xdirection has a constant velocity, so the only equation you need for that is x = v_xt.