AP Physics B Exam

17 Atomic and Nuclear Physics

INTRODUCTION

The subject matter of the previous chapters was developed in the seventeenth, eighteenth, and nineteenth centuries, but as we delve into the physics of the very small, we enter the twentieth century.

PHOTONS AND THE PHOTOELECTRIC EFFECT

The particle-like nature of light was revealed and studied through the work of Max Planck in 1900, and later Albert Einstein (who won the 1921 Nobel Prize for work in this area.) Electromagnetic radiation is emitted and absorbed by matter as though it existed in individual bundles calledquanta. A quantum of electromagnetic energy is known as a photon. Light behaves like a stream of photons, and this is illustrated by the photoelectric effect.

When a piece of metal is illuminated by electromagnetic radiation (specifically visible light, ultraviolet light, or X-rays), the energy absorbed by electrons near the surface of the metal can liberate them from their bound state, and these electrons can fly off. The released electrons are known as photoelectrons. In this case, the classical, wave-only theory of light would predict three results:

(1) There would be a significant time delay between the moment of illumination and the ejection of photoelectrons, as the electrons absorbed incident energy until their kinetic energy was sufficient to release them from the atoms” grip.

(2) Increasing the intensity of the light would cause the electrons to leave the metal surface with greater kinetic energy.

(3) Photoelectrons would be emitted regardless of the frequency of the incident energy, as long as the intensity was high enough.

Surprisingly, none of these predictions was observed. Photoelectrons were ejected within just a few billionths of a second after illumination, disproving prediction (1). Secondly, increasing the intensity of the light did not cause photoelectrons to leave the metal surface with greater kinetic energy. Although more electrons were ejected as the intensity was increased, there was a maximum photoelectron kinetic energy; prediction (2) was false. And, for each metal, there was a certain threshold frequency, f₀: If light of frequency lower than f₀ were used to illuminate the metal surface, no photoelectrons were ejected, regardless of how intense the incident radiation was; prediction (3) was also false. Clearly, something was wrong with the wave-only theory of light.

Einstein explained these observations by postulating that the energy of the incident electromagnetic wave was absorbed in individual bundles (photons). The energy of a photon is proportional to the frequency of the wave,

E = hf

where h is Planck”s constant (about 6.63 × 10^–34 J·s). A certain amount of energy had to be imparted to an electron on the metal surface in order to liberate it; this was known as the metal”s work function, or φ. If an electron absorbed a photon whose energy E was greater than φ, it would leave the metal with a maximum kinetic energy equal to E – φ. This process could occur very quickly, which accounts for the rapidity with which photoelectrons are produced after illumination.

Increasing the intensity of the incident energy means bombardment with more photons and results in the ejection of more photoelectrons—but since the energy of each incident photon is fixed by the equation E = hf, the value of K_max will still be E – φ. This can be expressed as

K_max = hf – φ

This accounts for the observation that disproved prediction (2).

Finally, if the incident energy had a frequency that was less than φ/h, the incident photons would each have an energy that was less than φ; this would not be enough energy to liberate electrons. Blasting the metal surface with more photons (that is, increasing the intensity of the incident beam) would also do nothing; none of the photons would have enough energy to eject electrons, so whether there were one or one million of them wouldn”t make any difference. This accounts for the observation of a threshold frequency, which we now know is φ/h. This can be expressed as

f_o = φ/h

Before we get to some examples, it”s worthwhile to introduce a new unit for energy. The SI unit for energy is the joule, but it”s too large to be convenient in the domains we”re studying now. We”ll use a much smaller unit, the electronvolt (abbreviated eV). The eV is equal to the energy gained (or lost) by an electron accelerated through a potential difference of one volt. Using the equation ∆U_E = qV, we find that

1 eV = (1 e)(1 V) = (1.6 × 10^–19 C)(1 V) = 1.6 × 10^–19 J

In terms of electronvolts, the value of Planck”s constant is 4.14 × 10^–15 eV·s.

Example 17.1 The work function, φ, for aluminum is 4.08 eV.

(a) What is the threshold frequency required to produce photoelectrons from aluminum?

(b) Classify the electromagnetic radiation that can produce photoelectrons.

(c) If light of frequency f = 4.00 × 10¹⁵ Hz is used to illuminate a piece of aluminum,

(i) what is K_max, the maximum kinetic energy of ejected photoelectrons?

(ii) what”s the maximum speed of the photoelectrons? (Electron mass = 9.11 × 10^–31 kg.)

(d) If the light described in part (b) were increased by a factor of 2 in intensity, what would happen to the value of K_max?

Solution.

(a) We know from the statement of the question that, in order for a photon to be successful in liberating an electron from the surface of the aluminum, its energy cannot be less than 4.08 eV. Therefore, the minimum frequency of the incident light—the threshold frequency—must be

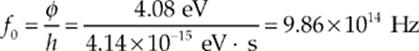
(b) Based on the electromagnetic spectrum given in the previous chapter, the electromagnetic radiation used to produce photoelectrons from aluminum must be at least in the ultraviolet region of the EM spectrum.

(c) (i) The maximum kinetic energy of photoelectrons is found from the equation

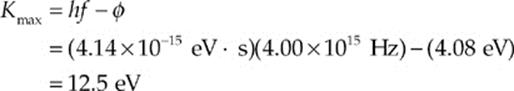
(ii) Using the above result and K = mv², we can find v_max:

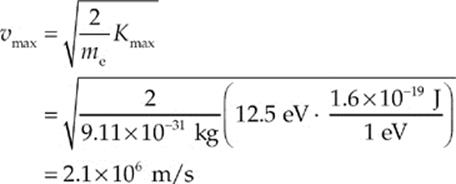
(d) Nothing will happen. Increasing the intensity of the illuminating radiation will cause more photons to impinge on the metal surface, thereby ejecting more photoelectrons, but their maximum kinetic energy will remain the same. The only way to increase K_max would be to increase the frequency of the incident energy.

THE BOHR MODEL OF THE ATOM

In the years immediately following Rutherford”s announcement of his nuclear model of the atom, a young physicist, Niels Bohr, would add an important piece to the atomic puzzle. Rutherford told us where the positive charge of the atom was located; Bohr would tell us about the electrons.

For fifty years it had been known that atoms in a gas discharge tube emit and absorb light only at specific wavelengths. The light from a glowing gas, passed through a prism to disperse the beam into its component wavelengths, produces patterns of sharp lines called atomic spectra. The visible wavelengths that appear in the emission spectrum of hydrogen had been summarized by the Balmer formula

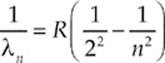
where R is the Rydberg constant (about 1.1 × 10⁷ m^–1). The formula worked—that is, it fit the observational data—but it had no theoretical basis. So, the question was, why do atoms emit (or absorb) radiation only at certain discrete wavelengths?

Bohr”s model of the atom explains the spectroscopists” observations. Using the simplest atom, hydrogen (with only one electron), Bohr postulated that the electron would orbit the nucleus only at certain discrete radii. When the electron is in one of these special orbits, it does not radiate away energy (as the classical theory would predict). However, if the electron absorbs a certain amount of energy, it is excited to a higher orbit, one with a greater radius. After a short time in this excited state, it returns to a lower orbit, emitting a photon in the process. Since each allowed orbit—or energy level—has a specific radius (and corresponding energy), the photons emitted in each jump have only specific wavelengths.

Bohr found that the energy of each excited state was a particular fraction of the energy of the ground state. Specifically, the energy of the nth energy level in hydrogen is given by the formula

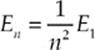
where E₁ is the ground-state energy, equal to –13.6 eV. The energy E₁(and, therefore, all the E_n) are negative. This corresponds to the fact that the electron is bound within the atom. Energy must be supplied to cause it to leave (ionizing the atom), bringing its energy to zero. For one-electron atoms, such as hydrogen, ionized helium (Z = 2), double-ionized lithium (Z = 3), etc., the value of the ground-state energy is also known as the ionization energy, the minimum amount of energy that must be supplied to release the atom”s electron. The energy levels for these atoms are given by

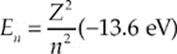
where Z is the number of protons in the atom”s nucleus.

When an excited electron drops from energy level n = j to a lower one, n = i, the transition causes a photon of energy to be emitted, and the energy of the photon is the difference between the two energy levels:

The wavelength of this photon is

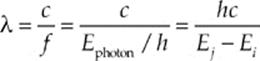
Example 17.2

The first five energy levels of an atom are shown in the diagram below:

(a) If the atom begins in the n = 3 level, what photon energies could be emitted as it returns to its ground state?

(b) What could happen if this atom, while in an undetermined energy state, were bombarded with a photon of energy 10 eV?

Solution.

(a) If the atom is in the n = 3 state, it could return to ground state by a transition from 3 → 1, or from 3 → 2 and then 2 → 1. The energy emitted in each of these transitions is simply the difference between the energies of the corresponding levels:

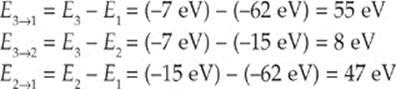
(b) Since no two energy levels in this atom are separated by 10 eV, the atom could not absorb a 10 eV photon, and as a result, nothing would happen. This atom would be transparent to light of energy 10 eV.

Example 17.3

(a) How much energy must a ground-state electron in a hydrogen atom absorb to be excited to the n = 4 energy level?

(b) With the electron in the n = 4 level, what wavelengths are possible for the photon emitted when the electron drops to a lower energy level? In what regions of the EM spectrum do these photons lie?

Solution.

(a) The ground-state energy level (n = 1) for hydrogen is –13.6 eV, and using the equation E_n = (1/n²)E₁, the n = 4 energy level (the third excited state) is

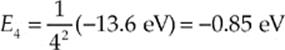
Therefore, in order for an electron to make the transition from E₁ to E₄, it must absorb energy in the amount E₄ – E₁ = (–0.85 eV) – (–13.6 eV) = 12.8 eV.

(b) An electron in the n = 4 energy level can make several different transitions: It can drop to n = 3, n = 2, or all the way down to the ground state, n = 1. The energies of the n = 2 and n = 3 levels are

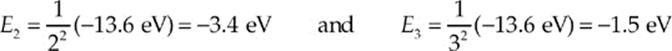
The following diagram shows the electron dropping from n = 4 to n = 3:

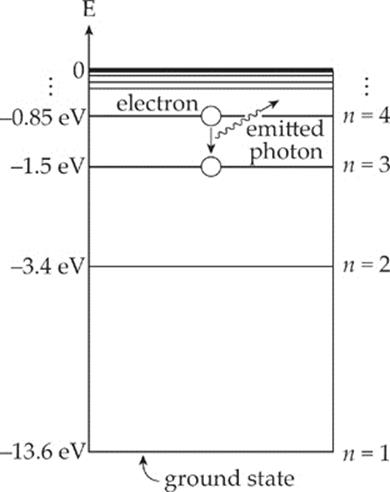
There are three possible values for the energy of the emitted photon, E_{4 → 3}, E_{4 → 2}, or E_{4 → 1}:

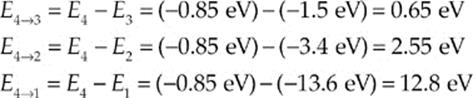
From the equation E = hf = hc/λ, we get λ = hc/E, so

Note that λ_{4 → 2} is in the visible spectrum; this wavelength corresponds to the color blue-green; λ_{4 → 3} is an ultraviolet wavelength, and λ_{4 → 3} is infrared.

WAVE-PARTICLE DUALITY

Light and other electromagnetic waves exhibit wave-like characteristics through interference and diffraction. However, as we saw in the photoelectric effect, light also behaves as if its energy were granular, composed of particles. This is wave-particle duality: Electromagnetic radiation propagates like a wave but exchanges energy like a particle.

Since an electromagnetic wave can behave like a particle, can a particle of matter behave like a wave? In 1923, the French physicist Louis de Broglie proposed that the answer is “yes.” His conjecture, which has since been supported by experiment, is that a particle of mass m and speed v—and thus with linear momentum p = mv—has an associated wavelength, which is called its de Broglie wavelength:

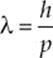
Particles in motion can display wave characteristics and behave as if they had a wavelength.

Since the value of h is so small, ordinary macroscopic objects do not display wave-like behavior. For example, a baseball (mass = 0.15 kg) thrown at a speed of 40 m/s has a de Broglie wavelength of

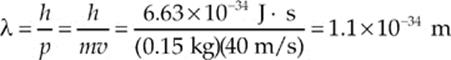
This is much too small to measure. However, with subatomic particles, the wave nature is clearly evident. The 1937 Nobel prize was awarded for experiments that revealed that a stream of electrons exhibited diffraction patterns when scattered by crystals—a behavior that”s characteristic of waves.

There”s an interesting connection between the de Broglie wavelength for electrons and Bohr”s model of quantized orbital radii (once tested on the AP Physics Exam!). Bohr postulated that the electron”s orbital angular momentum, m_ev_nr_n, had to be an integral multiple of ħ = . The equation

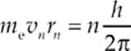
can be rewritten as follows:

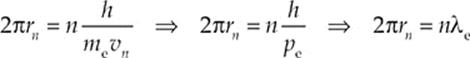
In this last form, the equation says that the circumference of the electron”s orbit must be equal to a whole number of wavelengths in order for it to be stable, a restriction that should remind you of sustained standing waves.

Example 17.4 Electrons in a diffraction experiment are accelerated through a potential difference of 200 V. What is the de Broglie wavelength of these electrons?

Solution. By definition, the kinetic energy of these electrons is 200 eV. Since the relationship between linear momentum and kinetic energy is p = ,

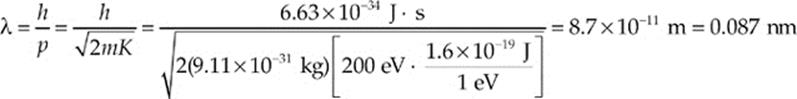
This wavelength is characteristic of X-rays.

NUCLEAR PHYSICS

The nucleus of the atom is composed of particles called protons and neutrons, which are collectively called nucleons. The number of protons in a given nucleus is called the atom”s atomic number, and is denoted Z, and the number of neutrons (the neutron number) is denoted N. The total number of nucleons, Z + N, is called the mass number (or nucleon number), and is denoted A. The number of protons in the nucleus of an atom defines the element. For example, the element chlorine (abbreviated Cl) is characterized by the fact that the nucleus of every chlorine atom contains 17 protons, so the atomic number of chlorine is 17; but, different chlorine atoms may contain different numbers of neutrons. In fact, about three-fourths of all naturally occurring chlorine atoms have 18 neutrons in their nuclei (mass number = 35), and most of the remaining one-fourth contain 20 neutrons (mass number = 37). Nuclei that contain the same numbers of protons but different numbers of neutrons are called isotopes. The notation for a nuclide—the term for a nucleus with specific numbers of protons and neutrons—is to write Z and A before the chemical symbol of the element:

The isotopes of chlorine mentioned above would be written as follows:

Example 17.5 How many protons and neutrons are contained in the nuclide ?

Solution. The subscript (the atomic number, Z) gives the number of protons, which is 29. The superscript (the mass number, A) gives the total number of nucleons. Since A = 63 = Z + N, we find that N = 63 – 29 = 34.

Example 17.6 The element neon (abbreviated Ne, atomic number 10) has several isotopes. The most abundant isotope contains 10 neutrons, and two others contain 11 and 12. Write symbols for these three nuclides.

Solution. The mass numbers of these isotopes are 10 + 10 = 20, 10 + 11 = 21, and 10 + 12 = 22. So, we”d write them as follows:

Another common notation—which we also use—is to write the mass number after the name of the element. These three isotopes of neon would be written as neon-20, neon-21, and neon-22.

THE NUCLEAR FORCE

Why wouldn”t any nucleus that has more than one proton be unstable? After all, protons are positively charged and would therefore experience a repulsive Coulomb force from each other. Why don”t these nuclei explode? And what holds neutrons—which have no electric charge—in the nucleus? These issues are resolved by the presence of another fundamental force, the strong nuclear force, which binds neutrons and protons together to form nuclei. Although the strength of the Coulomb force can be expressed by a simple mathematical formula (it”s inversely proportional to the square of their separation), the nuclear force is much more complicated; no simple formula can be written for the strength of the nuclear force.

BINDING ENERGY

The masses of the proton and neutron are listed below.

proton: m_p = 1.6726 × 10^–27 kg

neutron: m_n = 1.6749 × 10^–27 kg

Because these masses are so tiny, a much smaller mass unit is used. With the most abundant isotope of carbon (carbon-12) as a reference, the atomic mass unit (abbreviated amu or simply u) is defined as 1/12 the mass of a ¹²C atom. The conversion between kg and u is 1 u = 1.6605 × 10^–27kg. In terms of atomic mass units,

m_p = 1.00728 u

m_n = 1.00867 u

Now consider the deuteron, the nucleus of deuterium, an isotope of hydrogen that contains 1 proton and 1 neutron. The mass of a deuteron is 2.01356 u, which is a little less than the sum of the individual masses of the proton and neutron. The difference between the mass of any bound nucleus and the sum of the masses of its constituent nucleons is called the mass defect, ∆m. In the case of the deuteron (symbolized d), the mass defect is

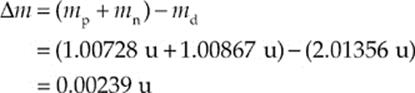
What happened to this missing mass? It was converted to energy when the deuteron was formed. It also represents the amount of energy needed to break the deuteron into a separate proton and neutron. Since this tells us how strongly the nucleus is bound, it is called the binding energy of the nucleus. The conversion between mass and energy is given by Einstein”s mass-energy equivalence equation, E = mc² (where c is the speed of light); the binding energy, E_B, is equal to the mass defect, ∆m:

E_B = (∆m)c²

Using E = mc², the energy equivalent of 1 atomic mass unit is

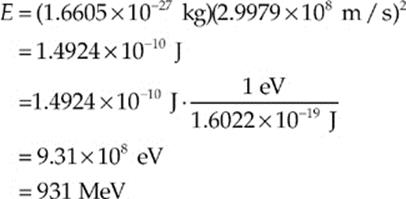
In terms of electronvolts, then, the binding energy of the deuteron is

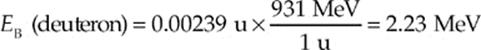
Since the deuteron contains 2 nucleons, the binding-energy-per-nucleon is

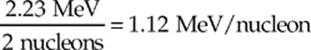
This is the lowest value of all nuclides. The highest, 8.8 MeV/nucleon, is for an isotope of nickel, ⁶²Ni. Typically, when nuclei smaller than nickel are fused to form a single nucleus, the binding energy per nucleon increases, which tells us that energy is released in the process. On the other hand, when nuclei larger than nickel are split, binding energy per nucleon again increases, releasing energy.

Example 17.7 What is the maximum wavelength of EM radiation that could be used to photodisintegrate a deuteron?

Solution. The binding energy of the deuteron is 2.23 MeV, so a photon would need to have at least this much energy to break the deuteron into a proton and neutron. Since E = hf and f = c/λ,

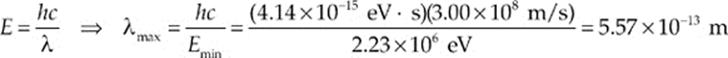
Example 17.8 The atomic mass of is 26.9815 u. What is its nuclear binding energy per nucleon? (Mass of electron = 0.0005486 u.)

Solution. The nuclear mass of is equal to its atomic mass minus the mass of its electrons. Since an aluminum atom has 13 protons, it must also have 13 electrons. So,

Now, the nucleus contains 13 protons and 27 – 13 = 14 neutrons, so the total mass of the individual nucleons is

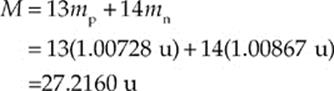
and, the mass defect of the aluminum nucleus is

∆m = M – m = 27.2160 u – 26.9744 u = 0.2416 u

Converting this mass to energy, we can see that

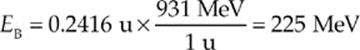
so the binding energy per nucleon is

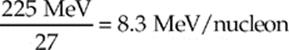
NUCLEAR REACTIONS

Natural radioactive decay provides one example of a nuclear reaction. Other examples of nuclear reactions include the bombardment of target nuclei with subatomic particles to artificially induce radioactivity, such as the emission of a particle or the splitting of the nucleus (this is nuclear fission), and the nuclear fusion of small nuclei at extremely high temperatures. In all cases of nuclear reactions that we”ll study, nucleon number and charge must be conserved. In order to balance nuclear reactions, we write or for a proton and for a neutron. Gamma-ray photons can also be produced in nuclear reactions; they have no charge or nucleon number and are represented as .

Example 17.9 A mercury-198 nucleus is bombarded by a neutron, which causes a nuclear reaction:

What”s the unknown product particle, X?

Solution. In order to balance the superscripts, we must have 1 + 198 = 197 + A, so A = 2, and the subscripts are balanced if 0 + 80 = 79 + Z, so Z = 1:

Therefore, X must be a deuteron, (or just d).

DISINTEGRATION ENERGY

Nuclear reactions not only produce new nuclei and other subatomic product particles, they also involve the absorption or emission of energy. Nuclear reactions must conserve total energy, so changes in mass are accompanied by changes in energy according to Einstein”s equation

∆E = (∆m)c²

A general nuclear reaction is written

A + B → C + D + Q

where Q denotes the disintegration energy. If Q is positive, the reaction is exothermic (or exoergic) and the reaction can occur spontaneously; if Q is negative, the reaction is endothermic (or endoergic) and the reaction cannot occur spontaneously. The energy Q is calculated as follows:

Q = [(m_A + m_B) – (m_C + m_D)]c² = (∆m)c²

For spontaneous reactions—ones that liberate energy—most of the energy is revealed as kinetic energy of the least massive product nuclei.

Example 17.10 The process that powers the Sun—and upon which all life on Earth is dependent—is the fusion reaction:

(a) Show that this reaction releases energy.

(b) How much energy is released per proton?

Use the fact that m_α = 4.0015 u and ignore the mass of the electron-neutrino, ν_e.

Solution.

(a) We need to find the mass difference between the reactants and products:

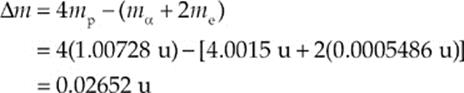
Since ∆m is positive, the reaction is exothermic: Energy is released.

(b) Converting the mass difference to energy gives

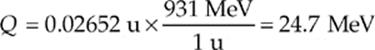
Since four protons went into the reaction, the energy liberated per proton is

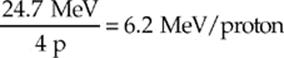
Example 17.11 Can the following nuclear reaction occur spontaneously?

(The mass of the nitrogen nucleus is 13.9992 u, and the mass of the oxygen nucleus is 16.9947 u.)

Solution. We first figure out the mass equivalent of the disintegration energy:

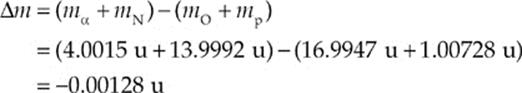
Since ∆m is negative, this reaction is nonspontaneous; energy must be supplied in order for this reaction to proceed. But how much?

CHAPTER 17 REVIEW QUESTIONS

Solutions can be found in Chapter 18.

SECTION I: MULTIPLE CHOICE

1. What”s the energy of a photon whose wavelength is 2.07 nm?

(A)   60 eV

(B)   600 eV

(C)   960 eV

(D)   6000 eV

(E)   9600 eV

2. A metal whose work function is 6.0 eV is struck with light of frequency 7.2 × 10¹⁵ Hz. What is the maximum kinetic energy of photoelectrons ejected from the metal”s surface?

(A)   7 eV

(B)   13 eV

(C)   19 eV

(D)   24 eV

(E)   No photoelectrons will be produced.

3. An atom with one electron has an ionization energy of 25 eV. How much energy will be released when the electron makes the transition from an excited energy level, where E = –16 eV, to the ground state?

(A)   9 eV

(B)   11 eV

(C)   16 eV

(D)   25 eV

(E)   41 eV

4. The single electron in an atom has an energy of –40 eV when it”s in the ground state, and the first excited state for the electron is at –10 eV. What will happen to this electron if the atom is struck by a stream of photons, each of energy 15 eV?

(A)   The electron will absorb the energy of one photon and become excited halfway to the first excited state, then quickly return to the ground state, without emitting a photon.

(B)   The electron will absorb the energy of one photon and become excited halfway to the first excited state, then quickly return to the ground state, emitting a 15 eV photon in the process.

(C)   The electron will absorb the energy of one photon and become excited halfway to the first excited state, then quickly absorb the energy of another photon to reach the first excited state.

(D)   The electron will absorb two photons and be excited to the first excited state.

(E)   Nothing will happen.

5. What is the de Broglie wavelength of a proton whose linear momentum has a magnitude of 3.3 × 10^–23 kg·m/s?

(A)   0.0002 nm

(B)   0.002 nm

(C)   0.02 nm

(D)   0.2 nm

(E)   2 nm

6. A partial energy-level diagram for an atom is shown below. What photon energies could this atom emit if it begins in the n = 3 state?

–3 eV __________________n=4

–5 eV __________________n=3

–8 eV __________________n=2

–12 eV __________________n=1 ground state

(A)   5 eV only

(B)   7 eV only

(C)   3 eV or 7 eV only

(D)   2 eV, 3 eV, or 7 eV

(E)   3 eV, 4 eV, or 7 eV

7. The ground-state energy level for He⁺ is –54.4 eV. How much energy must the electron in the ground state of He⁺ absorb in order to be excited to the next higher energy level?

(A)   13.6 eV

(B)   20.4 eV

(C)   27.2 eV

(D)   40.8 eV

(E)   68.0 eV

8. What would happen to the energy of a photon if its wavelength were reduced by a factor of 2?

(A)   It would decrease by a factor of 4.

(B)   It would decrease by a factor of 2.

(C)   It would increase by a factor of 2.

(D)   It would increase by a factor of 4.

(E)   It would increase by a factor of 2h.

9. In an exothermic nuclear reaction, the difference in mass between the reactants and the products is m, and the energy released is Q. In a separate exothermic nuclear reaction in which the mass difference between reactants and products is m/4, how much energy will be released?

(A)   Q/4

(B)   Q/2

(C)   (Q/4)c²

(D)   (Q/2)c²

(E)   4Q

10. What”s the missing particle in the following nuclear reaction?

(A)   proton

(B)   neutron

(C)   electron

(D)   positron

(E)   deuteron

11. What”s the missing particle in the following nuclear reaction?

(A)   proton

(B)   neutron

(C)   electron

(D)   positron

(E)   gamma

SECTION II: FREE RESPONSE

1. The Bohr model of electron energy levels can be applied to any one-electron atom, such as doubly ionized lithium (Li²⁺). The energy levels for the electron are given by the equation

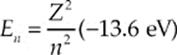
where Z is the atomic number. The emission spectrum for Li²⁺ contains four spectral lines corresponding to the following wavelengths:

11.4 nm, 13.5 nm, 54.0 nm, 72.9 nm

(a)   What”s the value of Z for Li²⁺?

(b)   Identify which energy-level transitions give rise to the four wavelengths cited.

(c)   Can the emission spectrum for Li²⁺ contain a line corresponding to a wavelength between 54.0 nm and 72.9 nm? If so, calculate its wavelength. If not, briefly explain.

(d)   What is the next shortest wavelength in the emission spectrum (closest to, but shorter than, 11.4 nm)?

SUMMARY

· The energy available to liberate electrons near the surface of a metal (the photoelectric effect) is proportional to the frequency of the incident photon. This idea is expressed in E = hf where h is Planck”s constant. (h = 6.63 × 10^–34J·s).

· The work function (φ) indicates the amount of energy needed to liberate the electron. There is a minimum frequency needed to liberate the electrons: f₀ = . The kinetic energy of the emitted electron is K_max = hf − φ.

· Particles in motion have wavelike properties: λ = where p is the momentum of the particle. Combining this with E = hf and c = fλ yields E = pc.

· Standard notation for an element is , where A is the mass number, Z is the number of protons in the nucleus, and A = Z+N, where N is the number of neutrons in the nucleus.

· A nuclear reaction produces new nuclei, other subatomic particles, and the absorption or emission of energy. The change in mass between the reactants and the products tells how much energy is released (exothermic or +Q) or how much energy is needed to produce the reaction (endothermic or –Q) in the general equation A + B → C + D + Q, where A and B are reactants and C and D are products. This energy released or absorbed is given by ΔE = (Δm)c².