AP Physics B Exam
3 Newton”s Laws
INTRODUCTION
In the previous chapter we studied the vocabulary and equations that describe motion. Now we will learn why things move the way they do; this is the subject of dynamics.
An interaction between two bodies—a push or a pull—is called a force. If you lift a book, you exert an upward force (created by your muscles) on it. If you pull on a rope that”s attached to a crate, you create a tension in the rope that pulls the crate. When a skydiver is falling through the air, the Earth is exerting a downward pull called gravitational force, and the air exerts an upward force called air resistance. When you stand on the floor, the floor provides an upward, supporting force called the normal force. If you slide a book across a table, the table exerts a frictional force against the book, so the book slows down and then stops. Static cling provides a directly observable example of the electrostatic force. Protons and neutrons are held together in the nuclei of atoms by the strong nuclear force and radioactive nuclei decay through the action of the weak nuclear force.
The Englishman Sir Isaac Newton published a book in 1687 called Philosophiae Naturalis Principa Mathematica (The Mathematical Principles of Natural Philosophy)—referred to nowadays as simply The Principia—which began the modern study of physics as a scientific discipline. Three of the laws that Newton stated in The Principia form the basis for dynamics and are known simply as Newton”s Laws of Motion.
THE FIRST LAW
Newton”s First Law says that an object will continue in its state of motion unless compelled to change by a force impressed upon it. That is, unless an unbalanced force acts on an object, the object”s velocity will not change: If the object is at rest, then it will stay at rest; and if it is moving, then it will continue to move at a constant speed in a straight line.
This property of objects, their natural resistance to changes in their state of motion, is called inertia. In fact, the First Law is often referred to as the Law of Inertia.
THE SECOND LAW
Newton”s Second Law predicts what will happen when an unbalanced force does act on an object: The object”s velocity will change; the object will accelerate. More precisely, it says that its acceleration, a, will be directly proportional to the strength of the total—or net—force (Fnet) and inversely proportional to the object”s mass, m:
Fnet = ma or Σ F = ma
This is the most important equation in mechanics!
The mass of an object is the quantitative measure of its inertia; intuitively, it measures how much matter is contained in an object. Two identical boxes, one empty and one full, have different masses. The box that”s full has the greater mass, because it contains more stuff; more stuff, more mass. Mass is measured in kilograms, abbreviated as kg. (Note: An object whose mass is 1 kg weighs about 2.2 pounds.) It takes twice as much force to produce the same change in velocity of a 2 kg object than of a 1 kg object. Mass is a measure of an object”s inertia, its resistance to acceleration.
Forces are represented by vectors; they have magnitude and direction. If several different forces act on an object simultaneously, then the net force, Fnet, is the vector sum of all these forces. (The phrase resultant force is also used to mean net force.)
Since Fnet = ma, and m is a positive scalar, the direction of a always matches the direction of Fnet. Finally, since F = ma, the units for F equal the units of m times the units of a:
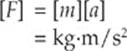
A force of 1 kg·m/s2 is renamed 1 newton (abbreviated as N). A medium-size apple weighs about 1 N.
THE THIRD LAW
This is the law that”s commonly remembered as, to every action, there is an equal, but opposite, reaction. More precisely, if Object 1 exerts a force on Object 2, then Object 2 exerts a force back on Object 1, equal in strength but opposite in direction. These two forces, F1-on-2 and F2-on-1, are called an action/reaction pair.
Example 3.1 What net force is required to maintain a 5000 kg object moving at a constant velocity of magnitude 7500 m/s?
Solution. The First Law says that any object will continue in its state of motion unless an unbalanced force acts on it. Therefore, no net force is required to maintain a 5000 kg object moving at a constant velocity of magnitude 7500 m/s.
You might be asking, “If no net force is needed to keep a car moving at a constant speed, why does the driver need to press down on the gas pedal in order to maintain a constant speed?” There is a big difference between force and net force. As the car moves forward, there is a frictional force (more on that shortly) opposite the direction of motion that would be slowing the car down. The gas supplies energy to the engine to spin the tires so they exert a forward force on the car to counteract friction and make the net force zero, which maintains a constant speed.
Here”s another way to look at it: Constant velocity means a = 0, so the equation Fnet = ma immediately gives Fnet = 0.
Example 3.2 How much force is required to cause an object of mass 2 kg to have an acceleration of 4 m/s2?
Solution. According to the Second Law, Fnet = ma = (2 kg)(4 m/s2) = 8 N.
Example 3.3 An object feels two forces; one of strength 8 N pulling to the left and one of strength 20 N pulling to the right. If the object”s mass is 4 kg, what is its acceleration?
Solution. Forces are represented by vectors and can be added and subtracted. Therefore, an 8 N force to the left added to a 20 N force to the right yields a net force of 20 – 8 = 12 N to the right. Then Newton”s Second Law gives a = Fnet/m = (12 N to the right)/(4 kg) = 3 m/s2 to the right.
WEIGHT
Mass and weight are not the same thing—there is a clear distinction between them in physics—but they are often used interchangeably in everyday life. The weight of an object is the gravitational force exerted on it by the Earth (or by whatever planet it happens to be on). Mass, by contrast, is an intrinsic property of an object that measures its inertia. An object”s mass does not change with location. Put a baseball in a rocket and send it to the Moon. The baseball”s weight on the Moon is less than its weight here on Earth (because the Moon”s gravitational pull is weaker than the Earth”s due to its much smaller mass), but the baseball”s mass would be the same.
Since weight is a force, we can use F = ma to compute it. What acceleration would the gravitational force impose on an object? The gravitational acceleration, of course! Therefore, setting a = g, the equation F = ma becomes
Fw = mg or Fg = mg
This is the equation for the weight of an object of mass m. (Weight is often symbolized as Fg, rather than Fw.) Notice that mass and weight are proportional but not identical. Furthermore, mass is measured in kilograms, while weight is measured in newtons.
Example 3.4 What is the mass of an object that weighs 500 N?
Solution. Since weight is m multiplied by g, mass is Fw (weight) divided by g. Therefore,
m = Fw/g = (500 N)/(10 m/s2) = 50 kg
Example 3.5 A person weighs 150 pounds. Given that a pound is a unit of weight equal to 4.45 N, what is this person”s mass?
Solution. This person”s weight in newtons is (150 lb)(4.45 N/lb) = 667.5 N, so his mass is
m = Fw/g = (667.5 N)/(10 m/s2) = 66.75 kg
Example 3.6 A book whose mass is 2 kg rests on a table. Find the magnitude of the force exerted by the table on the book.
Solution. The book experiences two forces: The downward pull of the Earth”s gravity and the upward, supporting force exerted by the table. Since the book is at rest on the table, its acceleration is zero, so the net force on the book must be zero. Therefore the magnitude of the support force must equal the magnitude of the book”s weight, which is Fw = mg = (2 kg)(10 m/s2) = 20 N.
AN OVERALL STRATEGY
The above examples are the lowest level of understanding Newton”s laws. They are pretty straightforward thinking sometimes referred to as “plug and chug.” Most of physics is not that simple. Frequently there is more than one force acting on an object and many times angles are involved. Following the below strategy can greatly increase your chance of success for all but the most trivial of Newton”s Second Law problems.
I. You must be able to visualize what”s going on. Make a sketch if it helps, but definitely make a free-body diagram by doing the following:
A. Draw a dot to represent the object. Draw arrows going away from the dot to represent any (all) forces acting on the object.
i. Anything touching the object exerts a force.
a. If the thing touching the object is a rope, ropes can only pull. Draw in the force accordingly.
b. If the thing touching the object is a table, ramp, floor, or some other flat surface, a surface can exert two forces.
1. The surface exerts a force perpendicular to itself toward the object. This force is always present if two things are in contact and is called the normal force.
2. If there is kinetic friction present, then the surface exerts a force on the object that is parallel to the surface and opposite to the direction of motion.
ii. Some things can exert a force without touching an object. For example, the Earth pulls down on everything via the mystery of gravity. Electricity and magnetism also exert their influences without actually touching. Unless you hear otherwise, gravity points down!
iii. If you know one force is bigger than another, you should draw that arrow longer than the smaller force.
iv. Don”t draw a velocity and mistake it for a force. No self-respecting velocity vector hangs out in a free-body diagram! Oh, and there is no such thing as the force of inertia.
II. Clearly define an appropriate coordinate system. Be sure to break up each force that does not lie on an axis into its x and y components.
III. Write out Newton”s Second Law in the form of ![]() and/or
and/or ![]() using the forces identified in the free-body diagram to fill in the appropriate forces.
using the forces identified in the free-body diagram to fill in the appropriate forces.
IV. Do the math.
As you go though the following examples, notice how this strategy is used.
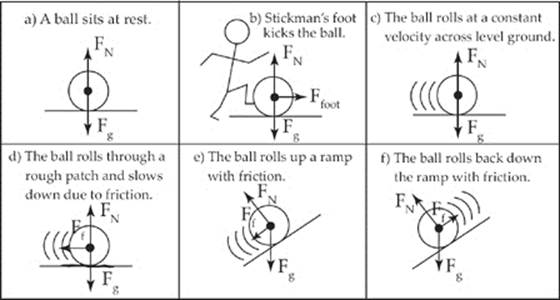
Example 3.7 Draw a free-body diagram for each of the following situations:

Solution. Notice that gravity always points down (even on ramps). Also the normal force is perpendicular to the surface (even on ramps). Do not always put the normal opposite the direction of gravity, because the normal is relative to the surface, which may be tilted. Finally, friction is always parallel to the surface (or perpendicular to the normal) and tends to point in the opposite direction from motion.
Example 3.8 A can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with an acceleration of 1 m/s2, what must the tension in the rope be?
Solution. First draw a picture. Represent the object of interest (the can of paint) as a heavy dot, and draw the forces that act on the object as arrows connected to the dot. This is called a free-body (or force) diagram.
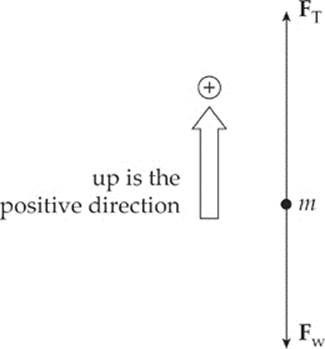
We have the tension force in the rope, FT (also symbolized merely by T), which is upward, and the weight, Fw, which is downward. Calling up the positive direction, the net force is FT – Fw. The Second Law, Fnet = ma, becomes FT – Fw = ma, so
FT = Fw + ma = mg + ma = m(g + a) = 6(10 + 1) = 66 N
Example 3.9 A can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with a constant velocity of 1 m/s, what must the tension in the rope be?
Solution. The phrase “constant velocity” automatically means a = 0 and, therefore, Fnet = 0. In the diagram above, FT would need to have the same magnitude as Fw in order to keep the can moving at a constant velocity. Thus, in this case, FT = Fw = mg = (6)(10) = 60 N.
Example 3.10 How much tension must a rope have to lift a 50 N object with an acceleration of 10 m/s2?
Solution. First draw a free-body diagram:
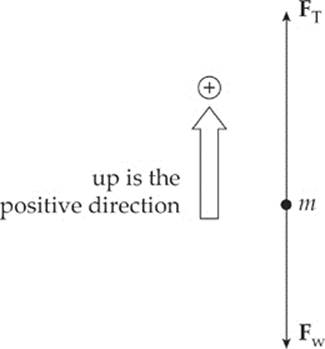
We have the tension force, FT, which is upward, and the weight, Fw, which is downward. Calling up the positive direction, the net force is FT – Fw. The Second Law, Fnet = ma, becomes FT – Fw = ma, so FT = Fw + ma. Remembering that m = Fw/g, we find that
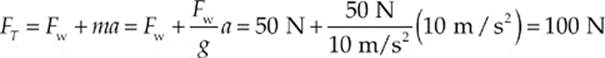
THE NORMAL FORCE
When an object is in contact with a surface, the surface exerts a contact force on the object. The component of the contact force that”s perpendicular to the surface is called the normal force on the object. (In physics, the word normal means perpendicular.) The normal force is what prevents objects from falling through tabletops or you from falling through the floor. The normal force is denoted by FN, or simply by N. (If you use the latter notation, be careful not to confuse it with N, the abbreviation for the newton.)
Example 3.11 A book whose mass is 2 kg rests on a table. Find the magnitude of the normal force exerted by the table on the book.
Solution. The book experiences two forces: The downward pull of Earth”s gravity and the upward, supporting force exerted by the table. Since the book is at rest on the table, its acceleration is zero, so the net force on the book must be zero. Therefore, the magnitude of the support force must equal the magnitude of the book”s weight, which is Fw = mg = (2)(10) = 20 N. This means the normal force must be 20 N as well: FN = 20 N. (Note that this is a repeat of Example 3.6, except now we have a name for the “upward, supporting force exerted by the table”; it”s called the normal force.)
FRICTION
When an object is in contact with a surface, the surface exerts a contact force on the object. The component of the contact force that”s parallel to the surface is called the friction force on the object. Friction, like the normal force, arises from electrical interactions between atoms of which the object is composed and those of which the surface is composed.
We”ll look at two main categories of friction: (1) static friction and (2) kinetic (sliding) friction. If you attempt to push a heavy crate across a floor, at first you meet with resistance, but then you push hard enough to get the crate moving. The force that acted on the crate to cancel out your initial pushes was static friction, and the force that acts on the crate as it slides across the floor is kinetic friction. Static friction occurs when there is no relative motion between the object and the surface (no sliding); kinetic friction occurs when there is relative motion (when there”s sliding).
The strength of the friction force depends, in general, on two things: The nature of the surfaces and the strength of the normal force. The nature of the surfaces is represented by the coefficient of friction, which is denoted by μ (mu) and has no units. The greater this number is, the stronger the friction force will be. For example, the coefficient of friction between rubber-soled shoes and a wooden floor is 0.7, but between rubber-soled shoes and ice, it”s only 0.1. Also, since kinetic friction is generally weaker than static friction (it”s easier to keep an object sliding once it”s sliding than it is to start the object sliding in the first place), there are two coefficients of friction; one for static friction (μs) and one for kinetic friction (μk). For a given pair of surfaces, it”s virtually always true that μk < μs. The strengths of these two types of friction forces are given by the following equations:
Fstatic friction, max = μsFN
Fkinetic friction = μkFN
Note that the equation for the strength of the static friction force is for the maximum value only. This is because static friction can vary, precisely counteracting weaker forces that attempt to move an object. For example, suppose an object experiences a normal force of FN = 100 N and the coefficient of static friction between it and the surface it”s on is 0.5. Then, the maximum force that static friction can exert is (0.5)(100 N) = 50 N. However, if you push on the object with a force of, say, 20 N, then the static friction force will be 20 N (in the opposite direction), not 50 N; the object won”t move. The net force on a stationary object must be zero. Static friction can take on all values, up to a certain maximum, and you must overcome the maximum static friction force to get the object to slide. The direction of Fkinetic friction = Ff (kinetic) is opposite to that of motion (sliding), and the direction of Fstatic friction = Ff (static) is usually, but not always, opposite to that of the intended motion.
Example 3.12 A crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
(a) Determine the strength of the friction force acting on the crate.
(b) If the crate is being pulled by a force of 90 N (parallel to the floor), find the acceleration of the crate.
Solution. First draw a free-body diagram:
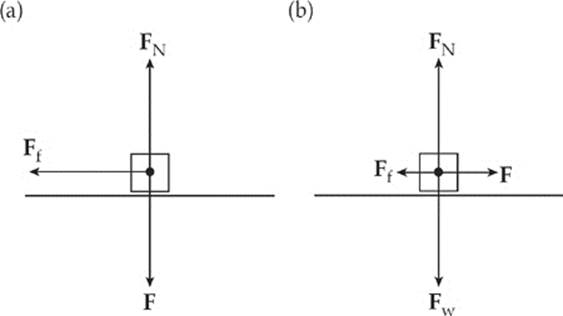
(a) The normal force on the object balances the object”s weight, so FN = mg = (20 kg)(10 m/s2) = 200 N. Therefore, F(kinetic) = μkFN = (0.3)(200 N) = 60 N.
(b) The net horizontal force that acts on the crate is F – Ff = 90 N – 60 N = 30 N, so the acceleration of the crate is a = Fnet/m = (30 N)/(20 kg)= 1.5 m/s2.
Example 3.13 A crate of mass 100 kg rests on the floor. The coefficient of static friction is 0.4. If a force of 250 N (parallel to the floor) is applied to the crate, what”s the magnitude of the force of static friction on the crate?
Solution. The normal force on the object balances its weight, so FN = mg = (100 kg)(10 m/s2) = 1,000 N. Therefore, Fstatic friction, max = Ff (static), max = μsFN = (0.4)(1,000 N) = 400 N. This is the maximum force that static friction can exert, but in this case it”s not the actual value of the static friction force. Since the applied force on the crate is only 250 N, which is less than the Ff (static), max, the force of static friction will be less also: Ff (static) = 250 N, and the crate will not slide.
PULLEYS
Pulleys are devices that change the direction of the tension force in the cords that slide over them. Here we”ll consider each pulley to be frictionless and massless, which means that their masses are so much smaller than the objects of interest in the problem that they can be ignored.
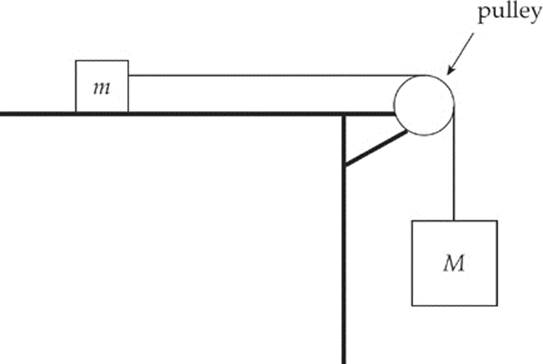
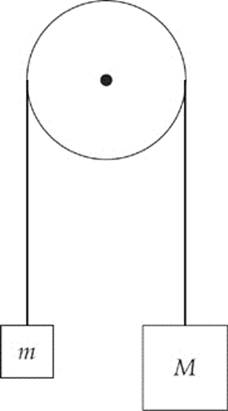
Example 3.14 In the diagram above, assume that the tabletop is frictionless. Determine the acceleration of the blocks once they”re released from rest.
Solution. There are two blocks, so we draw two free-body diagrams:
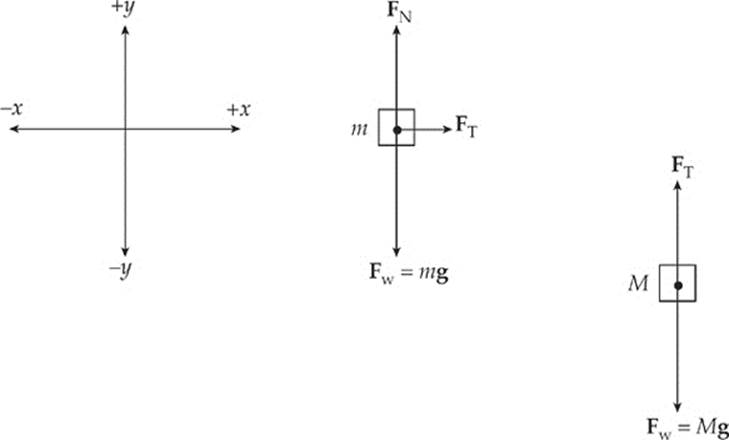
To get the acceleration of each one, we use Newton”s Second Law, Fnet = ma.
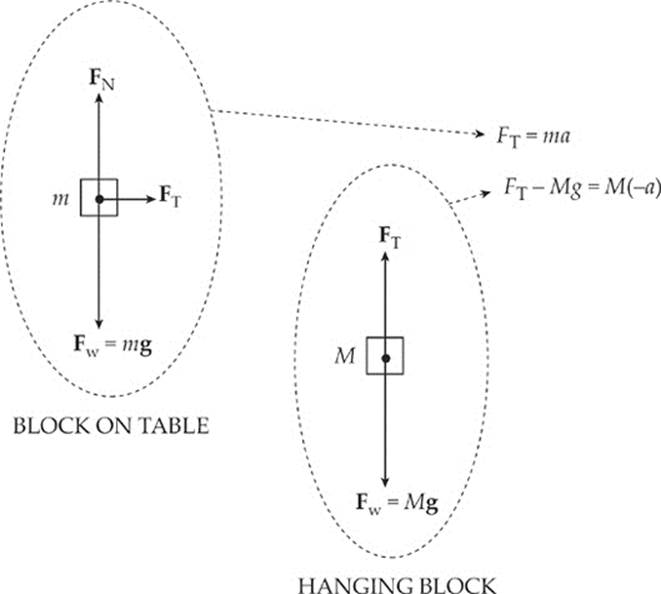
Note that there are two unknowns, FT and a, but we can eliminate FT by adding the two equations, and then we can solve for a.

Example 3.15 Using the same diagram as in the previous example, assume that m = 2 kg, M = 10 kg, and the coefficient of kinetic friction between the small block and the tabletop is 0.5. Compute the acceleration of the blocks.
Solution. Once again, draw a free-body diagram for each object. Note that the only difference between these diagrams and the ones in the previous example is the inclusion of the force of (kinetic) friction, Ff, that acts on the block on the table.
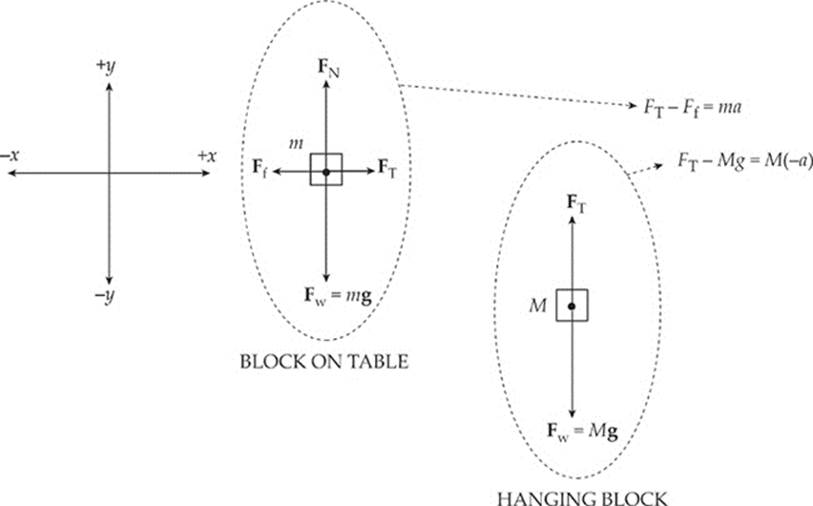
As before, we have two equations that contain two unknowns (a and FT):
FT – Ff = ma (1)
FT – Mg = M(–a) (2)
Subtract the equations (thereby eliminating FT) and solve for a. Note that, by definition, Ff = μFN, and from the free-body diagram for m, we see that FN = mg, so Ff = μmg:
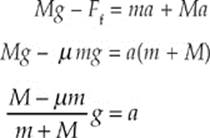
Substituting in the numerical values given for m, M, and μ, we find that a = ![]() g (or 7.5 m/s2).
g (or 7.5 m/s2).
Example 3.16 In the previous example, calculate the tension in the cord.
Solution. Since the value of a has been determined, we can use either of the two original equations to calculate FT. Using Equation (2), FT – Mg = M(–a) (because it”s simpler), we find
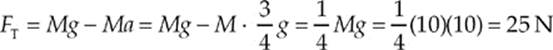
As you can see, we would have found the same answer if Equation (1) had been used:
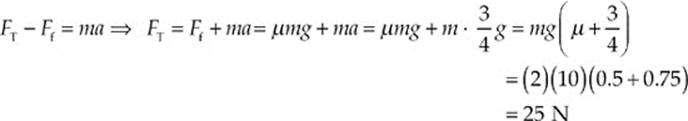
INCLINED PLANES
An inclined plane is basically a ramp. If you look at the forces acting on a block that sits on a ramp using a standard coordinate system it initially looks straight forward. However, part of the normal force acts in the x direction, part acts in the y direction, and the block has acceleration in both the x and y direction. If friction is present it also has components in both the x and y direction. The math has the potential to be quite cumbersome.
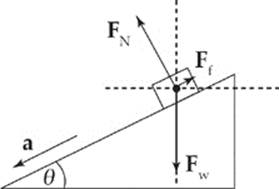
This is a non-rotated coordinate system—notice Ff, FN, and a will each have to be broken into x and y components.
However, if you rotate the coordinate system so that x is parallel to the ramp, gravity becomes split into components, but the normal force acts only in the y direction, friction acts only in the x direction, and the acceleration acts only in the x direction. This makes the math much cleaner.
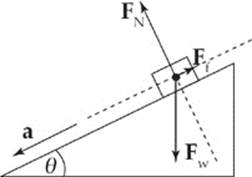
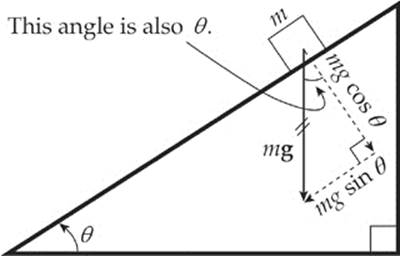
This is a rotated coordinate system—FN acts only in the y direction, Ff and the acceleration act only in the x direction and only Fw must be broken into components. If an object of mass m is on the ramp, then the force of gravity on the object, Fw = mg, has two components: One that”s parallel to the ramp (mg sin θ) and one that”s normal to the ramp (mg cos θ), where θ is the incline angle. The force driving the block down the inclined plane is the component of the block”s weight that”s parallel to the ramp: mg sin θ.
Example 3.17 A block slides down a frictionless, inclined plane that makes a 30° angle with the horizontal. Find the acceleration of this block.
Solution. Let m denote the mass of the block, so the force that pulls the block down the incline is mg sin θ, and the block”s acceleration down the plane is
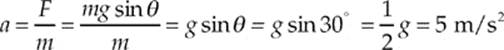
Example 3.18 A block slides down an inclined plane that makes a 30° angle with the horizontal. If the coefficient of kinetic friction is 0.3, find the acceleration of the block.
Solution. First draw a free-body diagram. Notice that, in the diagram shown below, the weight of the block, Fw = mg, has been written in terms of its scalar components: Fw sin θ parallel to the ramp and Fw cos θ normal to the ramp:
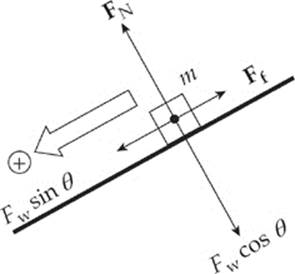
The force of friction, Ff, that acts up the ramp (opposite to the direction in which the block slides) has magnitude Ff = μFN. But the diagram shows that FN = Fw cos θ, so Ff = μ(mg cos θ). Therefore the net force down the ramp is
Fw sin θ – Ff = mg sin θ – μ mg cos θ = mg(sin θ – cos θ)
Then, setting Fnet equal to ma, we solve for a:
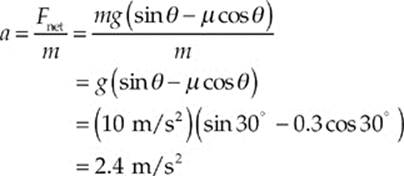
CHAPTER 3 REVIEW QUESTIONS
Solutions can be found in Chapter 18.
SECTION I: MULTIPLE CHOICE
1. A person standing on a horizontal floor feels two forces: the downward pull of gravity and the upward supporting force from the floor. These two forces
(A) have equal magnitudes and form an action/reaction pair
(B) have equal magnitudes but do not form an action/reaction pair
(C) have unequal magnitudes and form an action/reaction pair
(D) have unequal magnitudes and do not form an action/reaction pair
(E) none of the above
2. A person who weighs 800 N steps onto a scale that is on the floor of an elevator car. If the elevator accelerates upward at a rate of 5 m/s2, what will the scale read?
(A) 400 N
(B) 800 N
(C) 1000 N
(D) 1200 N
(E) 1600 N
3. A frictionless inclined plane of length 20 m has a maximum vertical height of 5 m. If an object of mass 2 kg is placed on the plane, which of the following best approximates the net force it feels?
(A) 5 N
(B) 10 N
(C) 15 N
(D) 20 N
(E) 30 N
4. A 20 N block is being pushed across a horizontal table by an 18 N force. If the coefficient of kinetic friction between the block and the table is 0.4, find the acceleration of the block.
(A) 0.5 m/s2
(B) 1 m/s2
(C) 5 m/s2
(D) 7.5 m/s2
(E) 9 m/s2
5. The coefficient of static friction between a box and a ramp is 0.5. The ramp”s incline angle is 30°. If the box is placed at rest on the ramp, the box will do which of the following?
(A) Accelerate down the ramp.
(B) Accelerate briefly down the ramp but then slow down and stop.
(C) Move with constant velocity down the ramp.
(D) Not move.
(E) It cannot be determined from the information given.
6.
Assuming a frictionless, massless pulley, determine the acceleration of the blocks once they are released from rest.
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
7. If all of the forces acting on an object balance so that the net force is zero, then
(A) the object must be at rest
(B) the object”s speed will decrease
(C) the object will follow a parabolic trajectory
(D) the object”s direction of motion can change, but not its speed
(E) None of the above will occur.
8. A block of mass m is at rest on a frictionless, horizontal table placed in a laboratory on the surface of the Earth. An identical block is at rest on a frictionless, horizontal table placed on the surface of the Moon. Let F be the net force necessary to give the Earth-bound block an acceleration of a across the table. Given that gMoon is one-sixth of gEarth, the force necessary to give the Moon-bound block the same acceleration a across the table is
(A) F/12
(B) F/6
(C) F/3
(D) F
(E) 6F
9. A crate of mass 100 kg is at rest on a horizontal floor. The coefficient of static friction between the crate and the floor is 0.4, and the coefficient of kinetic friction is 0.3. A force F of magnitude 344 N is then applied to the crate, parallel to the floor. Which of the following is true?
(A) The crate will accelerate across the floor at 0.5 m/s2.
(B) The static friction force, which is the reaction force to F as guaranteed by Newton”s Third Law, will also have a magnitude of 344 N.
(C) The crate will slide across the floor at a constant speed of 0.5 m/s.
(D) The crate will not move.
(E) None of the above
10. Two crates are stacked on top of each other on a horizontal floor; Crate #1 is on the bottom, and Crate #2 is on the top. Both crates have the same mass. Compared to the strength of the force F1 necessary to push only Crate #1 at a constant speed across the floor, the strength of the force F2 necessary to push the stack at the same constant speed across the floor is greater than F1because
(A) the normal force on Crate #1 is greater
(B) the coefficient of kinetic friction between Crate #1 and the floor is greater
(C) the force of kinetic friction, but not the normal force, on Crate #1 is greater
(D) the coefficient of static friction between Crate #1 and the floor is greater
(E) the weight of Crate #1 is greater
SECTION II: FREE RESPONSE
1. This question concerns the motion of a crate being pulled across a horizontal floor by a rope. In the diagram below, the mass of the crate is m, the coefficient of kinetic friction between the crate and the floor is μ, and the tension in the rope is FT.
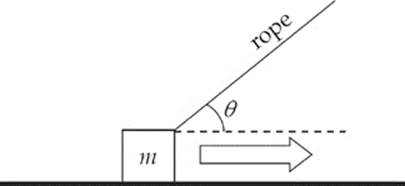
(a) Draw and label all of the forces acting on the crate.
(b) Compute the normal force acting on the crate in terms of m, FT, θ, and g.
(c) Compute the acceleration of the crate in terms of m, FT, θ, μ, and g.
2. In the diagram below, a massless string connects two blocks—of masses m1 and m2, respectively—on a flat, frictionless tabletop. A force F pulls on Block #2, as shown:
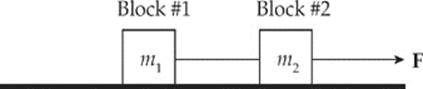
(a) Draw and label all of the forces acting on Block #1.
(b) Draw and label all of the forces acting on Block #2.
(c) What is the acceleration of Block #1?
(d) What is the tension in the string connecting the two blocks?
(e) If the string connecting the blocks were not massless, but instead had a mass of m, figure out
(i) the acceleration of Block #1, and
(ii) the difference between the strength of the force that the connecting string exerts on Block #2 and the strength of the force that the connecting string exerts on Block #1.
3. In the figure shown, assume that the pulley is frictionless and massless.
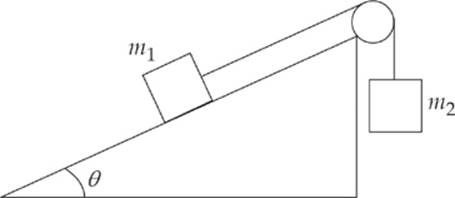
(a) If the surface of the inclined plane is frictionless, determine what value(s) of θ will cause the box of mass m1 to
(i) accelerate up the ramp;
(ii) slide up the ramp at constant speed.
(b) If the coefficient of kinetic friction between the surface of the inclined plane and the box of mass m1 is μk, derive (but do not solve) an equation satisfied by the value of θ which will cause the box of mass m1 to slide up the ramp at constant speed.
4. A sky diver is falling with speed v0 through the air. At that moment (time t = 0), she opens her parachute and experiences the force of air resistance whose strength is given by the equation F = kv, where k is a proportionality constant and v is her descent speed. The total mass of the sky diver and equipment is m. Assume that g is constant throughout her descent.
(a) Draw and label all the forces acting on the sky diver after her parachute opens.
(b) Determine the sky diver”s acceleration in terms of m, v, k, and g.
(c) Determine the sky diver”s terminal speed (that is, the eventual constant speed of descent).
(d) Sketch a graph of v as a function of time, being sure to label important values on the vertical axis.
SUMMARY
· Forces are not needed to maintain motion. Forces cause objects to change their motion, whether that means speeding up, slowing down, or changing direction. This idea is expressed by Newton”s Second Law: Fnet = ma.
· Weight is commonly referred to as the force of gravity Fw or Fg = mg where g is –10 m/s2.
· Friction is defined by Ff = μN and comes in two types—static and kinetic where μkinetic < μstatic.
· The normal force (N or sometimes FN) is frequently given by N or FN = mg cos θ, where θ is the angle between the horizontal axis and the surface on which the object rests.
· To solve almost any Newton”s Second Law problem, use the following strategy:
I. You must be able to visualize what”s going on. Make a sketch if it helps. Make sure to make a free-body diagram (or FBD).
II. Clearly define an appropriate coordinate system.
III. Write out Newton”s Second Law in the form of ![]() and/or
and/or ![]() using the forces identified in the FBD to fill in the appropriate forces.
using the forces identified in the FBD to fill in the appropriate forces.
IV. Do the math.