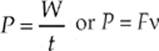AP Physics B Exam
4 Work, Energy, and Power
INTRODUCTION
It wasn”t until more than one hundred years after Newton that the idea of energy became incorporated into physics, but today it permeates every branch of the subject.
It”s difficult to give a precise definition of energy; there are different forms of energy because there are different kinds of forces. There”s gravitational energy and kinetic energy (a meteor crashing into the earth), elastic energy (a stretched rubber band), thermal energy (an oven), radiant energy (sunlight), electrical energy (a lamp plugged into a wall socket), nuclear energy (nuclear power plants), and mass energy (the heart of Einstein”s equation E = mc2). Energy can come into a system or leave it via various interactions that produce changes. One of the best definitions we know reads as follows: Force is the agent of change, energy is the measure of change, and work is the way of transferring energy from one system to another. And one of the most important laws in physics (the Law of Conservation of Energy, also known as the First Law of Thermodynamics) says that if you account for all its various forms, the total amount of energy in a given process will stay constant; that is, it will be conserved. For example, electrical energy can be converted into light and heat (this is how a light bulb works), but the amount of electrical energy coming in to the light bulb equals the total amount of light and heat given off. Energy cannot be created or destroyed; it can only be transferred (from one system to another) or transformed (from one form to another).
WORK
When you lift a book from the floor, you exert a force on it, over a distance, and when you push a crate across a floor, you also exert a force on it, over a distance. The application of force over a distance, and the resulting change in energy of the system that the force acted on, give rise to the concept of work. When you hold a book in your hand, you exert a force on the book (normal force) but, since the book is at rest, the force does not act through a distance, so you do no work on the book. Although you did work on the book as you lifted it from the floor, once it”s at rest in your hand, you are no longer doing work on it.
Definition. If a force F acts over a distance d, and F is parallel to d, then the work done by F is the product of force and distance: W = Fd.
Notice that, although work depends on two vectors (F and d), work itself is not a vector. Work is a scalar quantity.
Example 4.1 You slowly lift a book of mass 2 kg at constant velocity a distance of 3 m. How much work did you do on the book?
Solution. In this case, the force you exert must balance the weight of the book (otherwise the velocity of the book wouldn”t be constant), so F = mg = (2 kg)(10 m/s2) = 20 N. Since this force is straight upward and the displacement of the book is also straight upward, F and d are parallel, so the work done by your lifting force is W = Fd = (20 N)(3 m) = 60 N·m. The unit for work, the newton-meter (N·m) is renamed a joule, and abbreviated as J. So the work done here is 60 J.
The definition above takes care of cases in which F is parallel to the motion. If F is not parallel to the motion, then the definition needs to be generalized.
Definition. If a force F acts over a distance d, and θ is the angle between F and d, then the work done by F is the product of the component of force in the direction of the motion and the distance: W = (F cos θ)d.
Example 4.2 A 15 kg crate is moved along a horizontal floor by a warehouse worker who”s pulling on it with a rope that makes a 30° angle with the horizontal. The tension in the rope is 69 N and the crate slides a distance of 10 m. How much work is done on the crate by the worker?
Solution. The figure below shows that FT and d are not parallel. It”s only the component of the force acting along the direction of motion, FT cos θ, that does work.
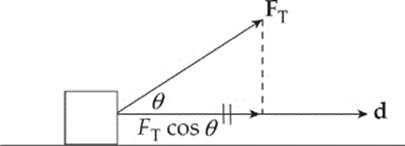
Therefore,
W = (FT cos θ)d = (69 N · cos 30°)(10 m) = 600 J
Example 4.3 In the previous example, assume that the coefficient of kinetic friction between the crate and the floor is 0.4.
(a) How much work is done by the normal force?
(b) How much work is done by the friction force?
Solution.
(a) Clearly, the normal force is not parallel to the motion, so we use the general definition of work. Since the angle between FN and d is 90° (by definition of normal) and cos 90° = 0, the normal force does zero work.
(b) The friction force, Ff, is also not parallel to the motion; it”s antiparallel. That is, the angle between Ff and d is 180°. Since cos 180° = –1, and since the strength of the normal force is FN = Fw = mg = (15 kg)(10 m/s2) = 150 N, the work done by the friction force is:
W = –Ffd = –µkFNd = –(0.4)(150 N)(10 m) = –600 J
Note that FT cosθ = 60 N
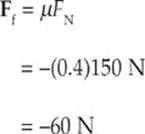
Therefore, Fnet = 0, as we expect.
The two previous examples show that work, which is a scalar quantity, may be positive, negative, or zero. If the angle between F and d(θ) is less than 90°, then the work is positive (because cos θ is positive in this case); if θ = 90°, the work is zero (because cos 90° = 0); and if θ > 90°, then the work is negative (because cos θ is negative). Intuitively, if a force helps the motion, the work done by the force is positive, but if the force opposes the motion, then the work done by the force is negative.
Example 4.4 A box slides down an inclined plane (incline angle = 37°). The mass of the block, m, is 35 kg, the coefficient of kinetic friction between the box and the ramp, µk, is 0.3, and the length of the ramp, d, is 8 m.

(a) How much work is done by gravity?
(b) How much work is done by the normal force?
(c) How much work is done by friction?
(d) What is the total work done?
Solution.
(a) Recall that the force that”s directly responsible for pulling the box down the plane is the component of the gravitational force that”s parallel to the ramp: Fw sin θ = mg sin θ (where θ is the incline angle). This component is parallel to the motion, so the work done by gravity is
Wby gravity = (mg sin θ)d = (35 kg)(10 N/kg)(sin 37°)(8 m) = 1690 J
Note that the work done by gravity is positive, as we would expect it to be, since gravity is helping the motion. Also, be careful with the angle θ. The general definition of work reads W = (F cos θ)d, where θ is the angle between F and d. However, the angle between Fw and d is not37° here, so the work done by gravity is not (mg cos 37°)d. The angle θ used in the calculation above is the incline angle.
(b) Since the normal force is perpendicular to the motion, the work done by this force is zero.
(c) The strength of the normal force is Fw cos θ (where θ is the incline angle), so the strength of the friction force is Ff = µkFN = µkFw cos θ = µkmg cos θ. Since Ff is antiparallel to d, the cosine of the angle between these vectors (180°) is –1, so the work done by friction is
Wby friction = –Ffd = –(µkmg cos θ)(d) = –(0.3)(35 kg)(10 N/kg)(cos 37°)(8 m) = –671 J
Note that the work done by friction is negative, as we expect it to be, since friction is opposing the motion.
(d) The total work done is found simply by adding the values of the work done by each of the forces acting on the box:
Wtotal = ΣW = Wby gravity + Wby normal force + Wby friction = 1690 + 0 + (–671) = 1019 J
WORK DONE BY A VARIABLE FORCE
If a force remains constant over the distance through which it acts, then the work done by the force is simply the product of force and distance. However, if the force does not remain constant, then the work done by the force is given by the area under the curve of a force vs. displacement graph. In physics language, the term “under the curve” really means between the line itself and zero.
Example 4.5 A spring exerts a force as shown on the graph below. How much work is done as the spring stretches from 20 to 40 cm?
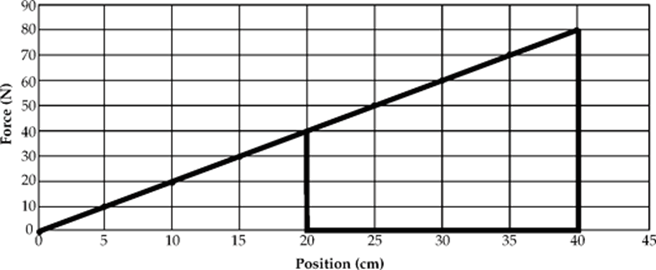
Solution. The area under the curve will be equal to the work done. In this case we have some choices. You may recognize this shape as a trapezoid (it might help to momentarily rotate your head, or this book, 90 degrees) to see this.
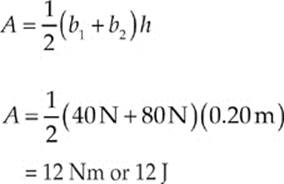
Similar to the previous chapter, units for work and energy should be confined to kg, m, and s, which is why we converted here.
An alternative choice is to recognize this shape as a triangle sitting on top of a rectangle. The total area is simply the area of the rectangle plus the area of the triangle.

KINETIC ENERGY
Consider an object at rest (v0 = 0), and imagine that a steady force is exerted on it, causing it to accelerate. Let”s be more specific; let the object”s mass be m, and let F be the force acting on the object, pushing it in a straight line. The object”s acceleration is a = F/m, so after the object has traveled a distance ∆x under the action of this force, its final speed, v, is given by Big Five #5:
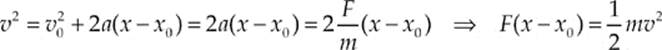
But the quantity F(x–x0) is the work done by the force, so W = ![]() mv2. The work done on the object has transferred energy to it, in the amount
mv2. The work done on the object has transferred energy to it, in the amount ![]() mv2. The energy an object possesses by virtue of its motion is therefore defined as
mv2. The energy an object possesses by virtue of its motion is therefore defined as ![]() mv2 and is called kinetic energy:
mv2 and is called kinetic energy:
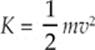
THE WORK–ENERGY THEOREM
Kinetic energy is expressed in joules, just like work, since in the case we just looked at, W = K. In fact, the derivation above can be extended to an object with a nonzero initial speed, and the same analysis will show that the total work done on an object—or, equivalently, the work done by the net force—will equal its change in kinetic energy; this is known as the work–energy theorem:
Wtotal = ∆K
Note that kinetic energy, like work, is a scalar quantity.
Example 4.6 What is the kinetic energy of a ball (mass = 0.10 kg) moving with a speed of 30 m/s?
Solution. From the definition,
![]()
Example 4.7 A tennis ball (mass = 0.06 kg) is hit straight upward with an initial speed of 50 m/s. How high would it go if air resistance were negligible?
Solution. This could be done using the Big Five, but let”s try to solve it using the concepts of work and energy. As the ball travels upward, gravity acts on it by doing negative work. [The work is negative because gravity is opposing the upward motion. Fw and d are in opposite directions, soθ = 180°, which tells us that W = (Fw cos θ)d = –Fwd.] At the moment the ball reaches its highest point, its speed is 0, so its kinetic energy is also 0. The work–energy theorem says
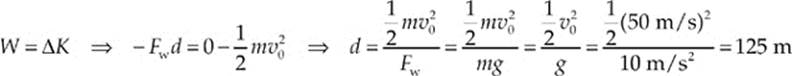
Example 4.8 Consider the box sliding down the inclined plane in Example 4.4. If it starts from rest at the top of the ramp, with what speed does it reach the bottom?
Solution. It was calculated in Example 4.4 that Wtotal = 1019 J. According to the work–energy theorem,
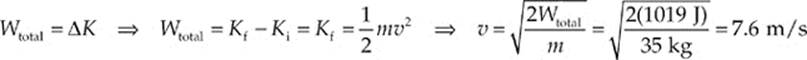
Example 4.9 A pool cue striking a stationary billiard ball (mass = 0.25 kg) gives the ball a speed of 2 m/s. If the average force of the cue on the ball was 200 N, over what distance did this force act?
Solution. The kinetic energy of the ball as it leaves the cue is

The work W done by the cue gave the ball this kinetic energy, so
![]()
POTENTIAL ENERGY
Kinetic energy is the energy an object has by virtue of its motion. Potential energy is independent of motion; it arises from the object”s position (or the system”s configuration). For example, a ball at the edge of a tabletop has energy that could be transformed into kinetic energy if it falls off. An arrow in an archer”s pulled-back bow has energy that could be transformed into kinetic energy if the archer releases the arrow. Both of these examples illustrate the concept of potential energy, the energy an object or system has by virtue of its position or configuration. In each case, work was done on the object to put it in the given configuration (the ball was lifted to the tabletop, the bowstring was pulled back), and since work is the means of transferring energy, these things have stored energy that can be retrieved, as kinetic energy. This is potential energy, denoted by U.
Because there are different types of forces, there are different types of potential energy. The ball at the edge of the tabletop provides an example of gravitational potential energy, Ug, which is the energy stored by virtue of an object”s position in a gravitational field. This energy would be converted to kinetic energy as gravity pulled the ball down to the floor. For now, let”s concentrate on gravitational potential energy.
Assume the ball has a mass m of 2 kg, and that the tabletop is h = 1.5 m above the floor. How much work did gravity do as the ball was lifted from the floor to the table? The strength of the gravitational force on the ball is Fw = mg = (2 kg)(10 N/kg) = 20 N. The force Fw points downward, and the ball”s motion was upward, so the work done by gravity during the ball”s ascent was
Wby gravity = –Fwh = –mgh = –(20 N)(1.5 m) = –30 J
So someone performed +30 J of work to raise the ball from the floor to the tabletop. That energy is now stored and, if the ball was given a push to send it over the edge, by the time the ball reached the floor it would acquire a kinetic energy of 30 J. We therefore say that the change in the ball”s gravitational potential energy in moving from the floor to the table was +30 J. That is,
∆Ug = –Wby gravity
Note that potential energy, like work (and kinetic energy), is expressed in joules.
In general, if an object of mass m is raised a height h (which is small enough that g stays essentially constant over this altitude change), then the increase in the object”s gravitational potential energy is
∆Ug = mgh
An important fact that makes the above equation possible is that the work done by gravity as the object is raised does not depend on the path taken by the object. The ball could be lifted straight upward, or in some curvy path; it would make no difference. Gravity is said to be a conservativeforce because of this property.
If we decide on a reference level to call h = 0, then we can say that the gravitational potential energy of an object of mass m at a height h is Ug = mgh. In order to use this last equation, it”s essential that we choose a reference level for height. For example, consider a passenger in an airplane reading a book. If the book is 1 m above the floor of the plane then, to the passenger, the gravitational potential energy of the book is mgh, where h = 1 m. However, to someone on the ground looking up, the floor of the plane may be, say, 9000 m above the ground. So, to this person, the gravitational potential energy of the book is mgH, where H = 9001 m. What both would agree on, though, is that the difference in potential energy between the floor of the plane and the position of the book is mg × (1 m), since the airplane passenger would calculate the difference as mg × (1 m – 0 m), while the person on the ground would calculate it as mg × (9001 m – 9000 m). Differences, or changes, in potential energy are unambiguous, but values of potential energy are relative.
Example 4.10 A stuntwoman (mass = 60 kg) scales a 40-meter-tall rock face. What is her gravitational potential energy (relative to the ground)?
Solution. Calling the ground h = 0, we find
Ug = mgh = (60 kg)(10 m/s2)(40 m) = 24,000 J
Example 4.11 If the stuntwoman in the previous example were to jump off the cliff, what would be her final speed as she landed on a large, air-filled cushion lying on the ground?
Solution. The gravitational potential energy would be transformed into kinetic energy. So
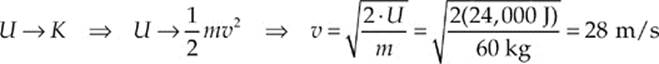
CONSERVATION OF MECHANICAL ENERGY
We have seen energy in its two basic forms: Kinetic energy (K) and potential energy (U). The sum of an object”s kinetic and potential energies is called its mechanical energy, E:
E = K + U
(Note that because U is relative, so is E.) Assuming that no nonconservative forces (friction, for example) act on an object or system while it undergoes some change, then mechanical energy is conserved. That is, the initial mechanical energy, Ei, is equal to the final mechanical energy, Ef, or
Ki + Ui = Kf + Uf
This is the simplest form of the Law of Conservation of Total Energy, which we mentioned at the beginning of this section.
Example 4.12 A ball of mass 2 kg is gently pushed off the edge of a tabletop that is 5.0 m above the floor. Find the speed of the ball as it strikes the floor.
Solution. Ignoring the friction due to the air, we can apply Conservation of Mechanical Energy. Calling the floor our h = 0 reference level, we write
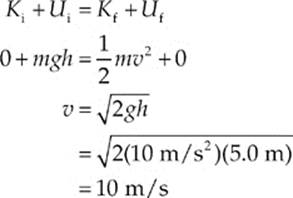
Note that the ball”s potential energy decreased, while its kinetic energy increased. This is the basic idea behind Conservation of Mechanical Energy: One form of energy decreases while the other increases.
Example 4.13 A box is projected up a long ramp (incline angle with the horizontal = 37°) with an initial speed of 10 m/s. If the surface of the ramp is very smooth (essentially frictionless), how high up the ramp will the box go? What distance along the ramp will it slide?
Solution. Because friction is negligible, we can apply Conservation of Mechanical Energy. Calling the bottom of the ramp our h = 0 reference level, we write
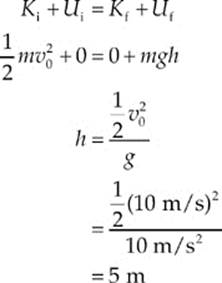
Since the incline angle is θ = 37°, the distance d it slides up the ramp is found in this way:
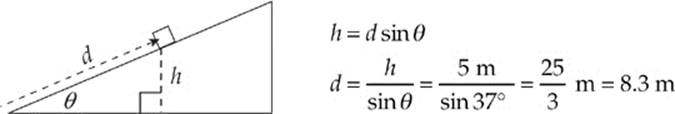
Example 4.14 A skydiver jumps from a hovering helicopter that”s 3000 meters above the ground. If air resistance can be ignored, how fast will he be falling when his altitude is 2000 m?
Solution. Ignoring air resistance, we can apply Conservation of Mechanical Energy. Calling the ground our h = 0 reference level, we write
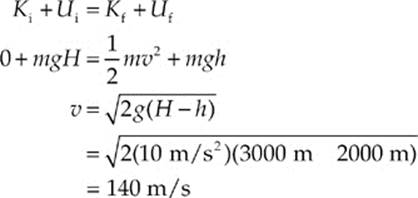
(That”s over 300 mph! This shows that air resistance does play a role, even before the parachute is opened.)
The equation Ki + Ui = Kf + Uf holds if no nonconservative forces are doing work. However, if work is done by such forces during the process under investigation, then the equation needs to be modified to account for this work as follows:
Ki + Ui + Wother = Kf + Uf
Example 4.15 Wile E. Coyote (mass = 40 kg) falls off a 50-meter-high cliff. On the way down, the force of air resistance has an average strength of 100 N. Find the speed with which he crashes into the ground.
Solution. The force of air resistance opposes the downward motion, so it does negative work on the coyote as he falls: Wr = –Frh. Calling the ground h = 0, we find that
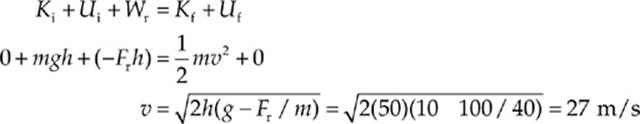
Example 4.16 A skier starts from rest at the top of a 20° incline and skis in a straight line to the bottom of the slope, a distance d (measured along the slope) of 400 m. If the coefficient of kinetic friction between the skis and the snow is 0.2, calculate the skier”s speed at the bottom of the run.
Solution. The strength of the friction force on the skier is Ff = µkFN = µk(mg cos θ), so the work done by friction is –Ff d = µk(mg cos θ)·d. The vertical height of the slope above the bottom of the run (which we designate the h = 0 level) is h = d sin θ. Therefore, Conservation of Mechanical Energy (including the negative work done by friction) gives
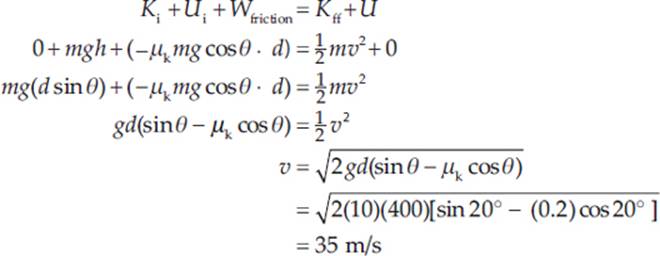
So far, any of the problems we have solved this chapter could have been solved using the kinematics equations and Newton”s Laws. The truly powerful thing about energy is that in a closed system, changes in energy are independent of the path you take. This allows you to solve many problems you would not otherwise be able to solve. With many energy problems you do not need to measure time with a stopwatch, you do not need to know the mass of the object, you do not need a constant acceleration (remember that is required for our Big Five equations from kinematics), and you do not need to know the path the object takes.
Example 4.17 A roller coaster at an amusement park is at rest on top of a 30 m hill (point A). The car starts to roll down the hill and reaches point B, which is 10 m above the ground, and then rolls up the track to point C, which is 20 m above the ground.
(a) A student assumes no energy is lost, and solves for how fast is the car moving at point C using energy arguments. What answer does he get?
(b) If the final speed at C is actually measured to be 2 m/s, what percentage of energy was “lost” and where did it go?
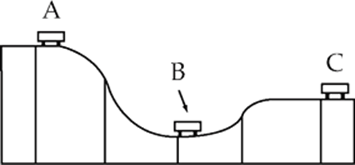
Solution.
(a) Our standard energy equation states
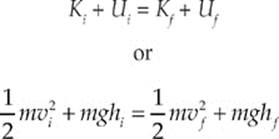
Canceling the mass, setting vi = 0 m/s and rearranging terms we get

(b) The initial energy of the system was all potential energy, that is,
Ei = mghi
The final energy of the system is given by
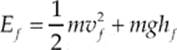
The percent of energy lost is given by the ratio of final energy to initial energy
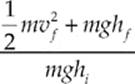
Canceling mass and substituting values yields

The other 32.7% was likely lost as heat.
It is worthy to note that the simplification of the energy equation to vf = ![]() can be used in quite a number of problems. It can also be inappropriately overused. The equation is valid only if the initial velocity is zero and there is no additional work being done such as a loss of energy due to frictional force, a collision that is not perfectly elastic, or some other applied force. In the above problem there was probably frictional force acting on the cart (which created the heat). Also, be careful about units. If gravity is being measured in meters per second squared, you must measure the change in height in meters.
can be used in quite a number of problems. It can also be inappropriately overused. The equation is valid only if the initial velocity is zero and there is no additional work being done such as a loss of energy due to frictional force, a collision that is not perfectly elastic, or some other applied force. In the above problem there was probably frictional force acting on the cart (which created the heat). Also, be careful about units. If gravity is being measured in meters per second squared, you must measure the change in height in meters.
POWER
Simply put, power is the rate at which work gets done (or energy gets transferred, which is the same thing). Suppose you and I each do 1000 J of work, but I do the work in 2 minutes while you do it in 1 minute. We both did the same amount of work, but you did it more quickly; you were more powerful. Here”s the definition of power:
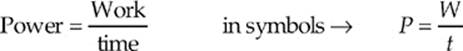
Because W = Fd cos θ, we could write P = 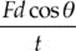 or P = F
or P = F![]() cos θ or P = Fv cos θ
cos θ or P = Fv cos θ
The unit of power is the joule per second (J/s), which is renamed the watt, and symbolized W (not to be confused with the symbol for work, W). One watt is 1 joule per second: 1 W = 1 J/s. Here in the United States, which still uses older units like inches, feet, yards, miles, ounces, pounds, and so forth, you still hear of power ratings expressed in horsepower (particularly of engines). One horsepower is defined as, well, the power output of a large horse. Horses can pull a 150-pound weight at a speed of 2![]() mph for quite a while. Let”s assume that F and d are parallel, so that
mph for quite a while. Let”s assume that F and d are parallel, so that
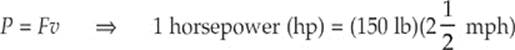
Now for some unit conversions:
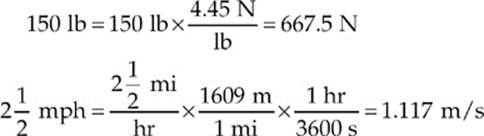
Therefore,
1 hp = (667.5 N)(1.117 m/s) = 746 W
By contrast, a human in good physical condition can do work at a steady rate of about 75 W (about 1/10 that of a horse!) but can attain power levels as much as twice this much for short periods of time.
Example 4.18 A mover pushes a large crate (mass m = 75 kg) from the inside of the truck to the back end (a distance of 6 m), exerting a steady push of 300 N. If he moves the crate this distance in 20 s, what is his power output during this time?
Solution. The work done on the crate by the mover is W = Fd = (300 N)(6 m) = 1800 J. If this much work is done in 20 s, then the power delivered is P = W/t = (1800 J)/(20 s) = 90 W.
Example 4.19 What must be the power output of an elevator motor that can lift a total mass of 1000 kg and give the elevator a constant speed of 8.0 m/s?
Solution. The equation P = Fv, with F = mg, yields
P = mgv = (1000 kg)(10 N/kg)(8.0 m/s) = 80,000 W = 80 kW
CHAPTER 4 REVIEW QUESTIONS
Solutions can be found in Chapter 18.
SECTION I: MULTIPLE CHOICE
1. A force F of strength 20 N acts on an object of mass 3 kg as it moves a distance of 4 m. If F is perpendicular to the 4 m displacement, the work it does is equal to
(A) 0 J
(B) 60 J
(C) 80 J
(D) 600 J
(E) 2400 J
2. Under the influence of a force, an object of mass 4 kg accelerates from 3 m/s to 6 m/s in 8 s. How much work was done on the object during this time?
(A) 27 J
(B) 54 J
(C) 72 J
(D) 96 J
(E) Cannot be determined from the information given
3. A box of mass m slides down a frictionless inclined plane of length L and vertical height h. What is the change in its gravitational potential energy?
(A) –mgL
(B) –mgh
(C) –mgL/h
(D) –mgh/L
(E) –mghL
4. An object of mass m is traveling at constant speed v in a circular path of radius r. How much work is done by the centripetal force during one-half of a revolution?
(A) π mv2
(B) 2π mv2
(C) 0
(D) π mv2r
(E) 2π mv2r
5. While a person lifts a book of mass 2 kg from the floor to a tabletop, 1.5 m above the floor, how much work does the gravitational force do on the book?
(A) –30 J
(B) –15 J
(C) 0 J
(D) 15 J
(E) 30 J
6. A block of mass 3.5 kg slides down a frictionless inclined plane of length 6.4 m that makes an angle of 30° with the horizontal. If the block is released from rest at the top of the incline, what is its speed at the bottom?
(A) 5.0 m/s
(B) 5.7 m/s
(C) 6.4 m/s
(D) 8.0 m/s
(E) 10 m/s
7. A block of mass m slides from rest down an inclined plane of length s and height h. If F is the magnitude of the force of kinetic friction acting on the block as it slides, then the kinetic energy of the block when it reaches the bottom of the incline will be equal to
(A) mgh
(B) mgh – Fh
(C) mgs – Fh
(D) mgh – Fs
(E) mgs – Fs
8. As a rock of mass 4 kg drops from the edge of a 40-meter-high cliff, it experiences air resistance, whose average strength during the descent is 20 N. At what speed will the rock hit the ground?
(A) 8 m/s
(B) 10 m/s
(C) 12 m/s
(D) 16 m/s
(E) 20 m/s
9. An astronaut drops a rock from the top of a crater on the Moon. When the rock is halfway down to the bottom of the crater, its speed is what fraction of its final impact speed?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
10. A force of 200 N is required to keep an object sliding at a constant speed of 2 m/s across a rough floor. How much power is being expended to maintain this motion?
(A) 50 W
(B) 100 W
(C) 200 W
(D) 400 W
(E) Cannot be determined from the information given
SECTION II: FREE RESPONSE
1. A box of mass m is released from rest at Point A, the top of a long, frictionless slide. Point A is at height H above the level of Points B and C. Although the slide is frictionless, the horizontal surface from Point B to C is not. The coefficient of kinetic friction between the box and this surface is µk, and the horizontal distance between Point B and C is x.
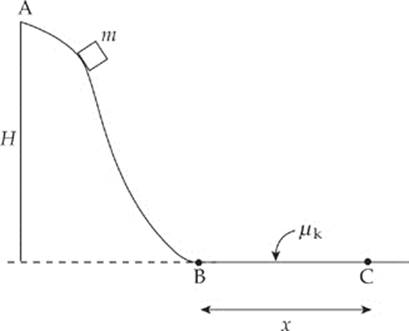
(a) Find the speed of the box when its height above Point B is H.
(b) Find the speed of the box when it reaches Point B.
(c) Determine the value of µk so that the box comes to rest at Point C.
(d) Now assume that Points B and C were not on the same horizontal level. In particular, assume that the surface from B to C had a uniform upward slope so that Point C were still at a horizontal distance of x from B but now at a vertical height of y above B. Answer the question posed in part (c).
(e) If the slide were not frictionless, determine the work done by friction as the box moved from Point A to Point B if the speed of the box as it reached Point B were half the speed calculated in part (b).
2. The diagram below shows a roller-coaster ride, which contains a circular loop of radius r. A car (mass m) begins at rest from Point A and moves down the frictionless track from A to B where it then enters the vertical loop (also frictionless), traveling once around the circle from B to C to D to E and back to B, after which it travels along the flat portion of the track from B to F (which is not frictionless).
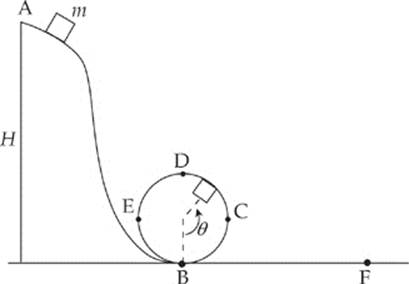
(a) Find the centripetal acceleration of the car when it is at Point C.
(b) What is the minimum cut-off speed vc that the car must have at Point D to make it around the loop?
(c) What is the minimum height H necessary to ensure that the car makes it around the loop?
(d) If H = 6r and the coefficient of friction between the car and the flat portion of the track from B to F is 0.5, how far along this flat portion of the track will the car travel before coming to rest at Point F?
3. A student uses a digital camera and computer to collect the following data about a ball as it slides down a curved frictionless track. The initial release point is 1.5 meters above the ground and the ball is released from rest. He prints up the following data and then tries to analyze it.
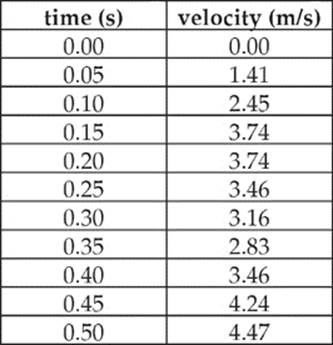
(a) Based on the data, what are the corresponding heights for each data point?
(b) What time segment experiences the greatest acceleration and what is the value of this acceleration?
(c) How would the values change if the mass of the ball were doubled?
SUMMARY
· Work is force applied across a displacement. Work can cause a change in energy. Positive work puts energy into a system, while negative work takes energy out of a system. Basic equations for work include:
![]()
· Energy is a conserved quantity. By that we mean the total initial energy is equal to the total final energy. Basic equations with energy include:
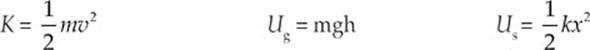
· Often, we limit ourselves to mechanical energy with no heat lost or gained. In this case:
Ki + Ui ± W = Kf + Uf
· Power is the rate at which one does work and is given by: