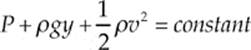AP Physics B Exam
8 Fluid Mechanics
INTRODUCTION
In this chapter, we”ll discuss some of the fundamental concepts dealing with substances that can flow, which are known as fluids. Although both liquids and gases are fluids, there are distinctions between them. At the molecular level, a substance in the liquid phase is similar to one in the solid phase in that the molecules are close to—and interact with—one another. The molecules in a liquid are able to move around a little more freely than those in a solid, where the molecules typically only vibrate around relatively fixed positions. By contrast, the molecules of a gas are not constrained and fly around in a chaotic swarm, with hardly any interaction. On a macroscopic level, there is also a distinction between liquids and gases. If you pour a certain volume of a liquid into a container, the liquid will occupy that same volume, whatever the shape of the container. However, if you introduce a sample of gas into a container, the molecules will fly around and fill the entire container.
DENSITY
Although the concept of mass was central to our study of mechanics in the preceding chapters (because of the all-important equation Fnet = ma), it is the substance”s density that turns out to be more useful in fluid mechanics.
By definition, the density of a substance is its mass per unit volume, and it”s typically denoted by the letter ρ (the Greek letter rho):
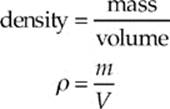
Note that this equation immediately implies that m is equal to ρV.
For example, if 10–3 m3 of oil has a mass of 0.8 kg, then the density of this oil is
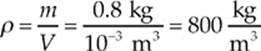
An old-fashioned but still very common way of expressing the density of a substance is to relate it to the density of water. The ratio of the density of any substance to the density of water is known as the specific gravity of the substance, abbreviated sp. gr.:
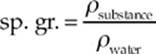
For example, if a substance has twice the density of water, we”d say that its specific gravity is 2. If the specific gravity is less than 1, this means the substance is less dense than water; if the specific gravity is greater than 1, then the substance is denser than water.
The density of liquid water is taken to be a constant, equal to 1000 kg/m3. So, for example, if a certain type of oil has a density of 800 kg/m3, then its specific gravity is
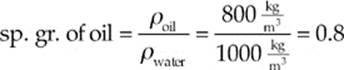
Note: Because it is a ratio of densities, sp. gr. has no units.
Example 8.1 Turpentine has a specific gravity of 0.9. What is its density?
Solution. We can use the equation for specific gravity to find that
![]()
Example 8.2 A cork has a volume of 4 cm3 and weighs 10–2 N. What is the specific gravity of cork?
Solution. Because the cork weighs 10–2 N, it has a mass of
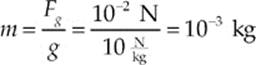
Its density is therefore
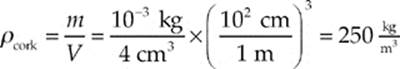
This means that the specific gravity of the cork is
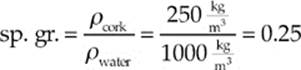
PRESSURE
If we place an object in a fluid, the fluid exerts a contact force on the object. How that force is distributed over any small area of the object”s surface defines the pressure:
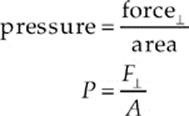
The subscript ⊥ (which means perpendicular) is meant to emphasize that the pressure is defined to be the magnitude of the force that acts perpendicular to the surface, divided by the area. Because force is measured in newtons (N) and area is expressed in square meters (m2), the SI unit for pressure is the newton per square meter. This unit is given its own name: the pascal, abbreviated Pa:
![]()
One pascal is a very tiny amount of pressure; for example, a nickel on a table exerts about 140 Pa of pressure, just due to its weight alone. For this reason, you”ll often see pressures expressed in kPa (kilopascals, where 1 kPa = 103 Pa) or even in MPa (megapascals, where 1 MPa = 106 Pa). Another common unit for pressure is the atmosphere (atm). At sea level, atmospheric pressure, Patm, is about 101,300 Pa; this is 1 atmosphere.
Example 8.3 A vertical column made of cement has a base area of 0.5 m2. If its height is 2 m, and the specific gravity of cement is 3, how much pressure does this column exert on the ground?
Solution. The force the column exerts on the ground is equal to its weight, mg, so we”ll find the pressure it exerts by dividing this by the base area, A. The mass of the column is equal to ρV, which we calculate as follows:
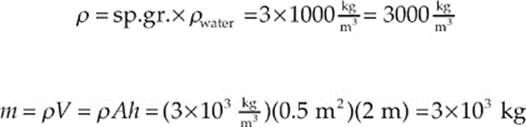
Therefore,
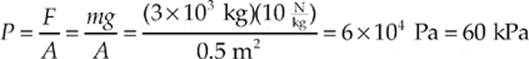
HYDROSTATIC PRESSURE
Imagine that we have a tank with a lid on top, filled with some liquid. Suspended from this lid is a string, attached to a thin sheet of metal. The figures below show two views of this:
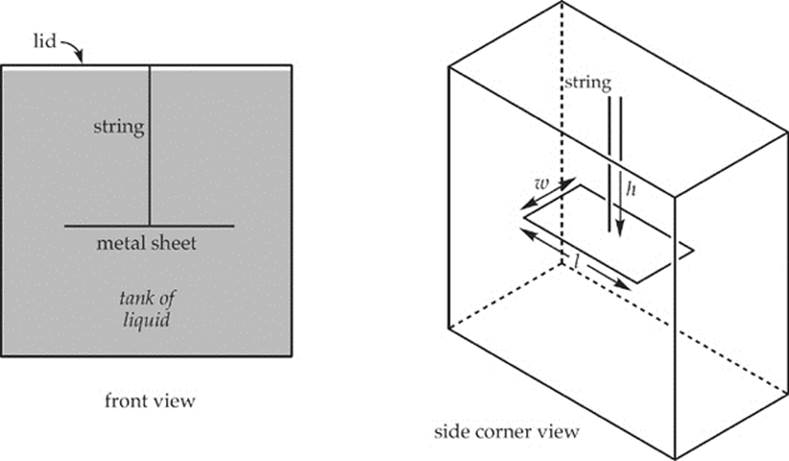
The weight of the liquid produces a force that pushes down on the metal sheet. If the sheet has length l and width w, and is at depth h below the surface of the liquid, then the weight of the liquid on top of the sheet is
Fg = mg = ρVg = ρ(lwh)g
where ρ is the liquid”s density. If we divide this weight by the area of the sheet (A = lw), we get the pressure due to the liquid:
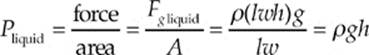
Since the liquid is at rest, this is known as hydrostatic pressure.
Note that the hydrostatic pressure due to the liquid, Pliquid = ρgh, depends only on the density of the liquid and the depth below the surface; in fact, it”s proportional to both of these quantities. One important consequence of this is that the shape of the container doesn”t matter. For example, if all the containers in the figure below are filled with the same liquid, then the pressure is the same at every point along the horizontal dashed line (and within a container), simply because every point on this line is at the same depth, h, below the surface of the liquid.
If the liquid in the tank were open to the atmosphere, then the total (or absolute) pressure at depth h would be equal to the pressure pushing down on the surface—the atmospheric pressure, Patm—plus the pressure due to the liquid alone:
total (absolute) pressure: Ptotal = Patm + Pliquid = Patm + ρgh
The difference between total pressure and atmospheric pressure is known as the gauge pressure:
Pgauge = P – Patm
So, another way of writing the equation above is to say:
Pgauge = ρgh
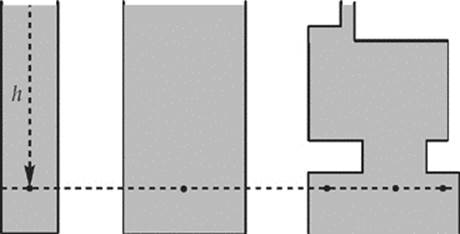
The following graphs show how gauge pressure and total pressure vary with depth. Note that although both graphs are straight lines, only gauge pressure is proportional to depth. In order for a graph to represent a direct proportion, it must be a straight line through the origin.
The lines will be straight as long as the density of the liquid remains constant as the depth increases. Actually, ρ increases as the depth increases, but the effect is small enough that we generally consider liquids to be incompressible—that is, that the density of a liquid remains constant and does not increase with depth.
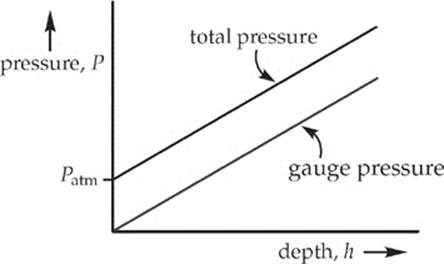
If we have a container of liquid where the pressure above the surface of the liquid is P0, then the total pressure at depth h below the surface would be P0 plus the pressure due just to the liquid:
If there”s no lid, then P0 = Patm, and we get the equation P = Patm + ρgh again.
Because pressure is the magnitude of the force per area, pressure is a scalar. It has no direction. The direction of the force due to the pressure on any small surface is perpendicular to that surface. For example, in the figure below, the pressure at Point A is the same as the pressure at Point B, because they”re at the same depth.
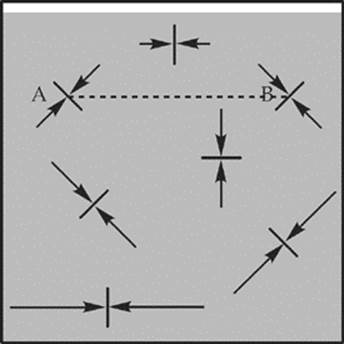
But, as you can see, the direction of the force due to the pressure varies depending on the orientation of the surface—and even which side of the surface—the force is pushing on.
Example 8.4 What is the hydrostatic gauge pressure at a point 10 m below the surface of the ocean? (Note: The specific gravity of seawater is 1.025.)
Solution. Using ρseawater = sp. gr. × ρwater = 1025 kg/m3, we find that
![]()
Note that this is just about equal to one atmosphere (1 atm = 1.013 × 105 Pa). In fact, a rule of thumb used by scuba and deep-sea divers is that the pressure increases by about 1 atmosphere for every 10 m (or 30.5 feet) of depth.
Example 8.5 A swimming pool has a depth of 4 m. What is the hydrostatic gauge pressure at a point 1 m below the surface?
Solution. Using ρ = ρwater = 1000 kg/m3 for the density of the pool water, we find that
![]()
Note that the total depth of the swimming pool is irrelevant; all that matters is the depth below the surface.
Example 8.6 What happens to the gauge pressure if we double our depth below the surface of a liquid? What happens to the total pressure?
Solution. Since Pgauge = ρgh, we see that Pgauge is proportional to the depth, h. Therefore, if we double h, then Pgauge will double. However, the total pressure, Patm + ρgh, is not proportional to h. The term ρgh will double, but the term Patm, being a constant, will not. So, the total pressure will increase, but it will not double; in fact, it will increase by less than a factor of 2.
Example 8.7 A flat piece of wood, of area 0.5 m2, is lying at the bottom of a lake. If the depth of the lake is 30 m, what is the force on the wood due to the pressure? (Use Patm = 1 × 105 Pa.)
Solution. Using ρ = ρwater = 1000 kg/m3 for the density of the water in the lake, we find that
![]()
Therefore, the total pressure on the wood is P = Patm + Pgauge = 4 × 105 Pa. Now, by definition, we have P = F/A, so F = PA; this gives
F = PA = (4 × 105 Pa)(0.5 m2) = 2 × 105 N
Example 8.8 Consider a closed container, partially filled with a liquid of density ρ = 1200 kg/m3, and a Point X that”s 0.5 m below the surface of the liquid.
(a) If the space above the surface of the liquid is vacuum, what”s the absolute pressure at Point X?
(b) If the space above the surface of the liquid is occupied by a gas whose pressure is 2.4 × 104 Pa, what”s the absolute pressure at Point X?
Solution.
(a) The absolute pressure at X is equal to the pressure pushing down on the surface of the liquid plus the pressure due to the liquid alone: P = P0 + ρgh. However, since the space above the liquid is vacuum, we have P0 = 0, so
![]()
(b) In this case, P0 = 2.4 × 104 Pa, so
P = P0 + ρgh = (2.4 × 104 Pa)(6 × 103 Pa) = 3 × 104 Pa
BUOYANCY
Let”s place a block in our tank of fluid. Because the pressure on each side of the block depends on its average depth, we see that there”s more pressure on the bottom of the block than there is on the top. Therefore, there”s a greater force pushing up on the block than there is pushing down on it. The forces due to the pressure on the other four sides (left and right, front and back) cancel out, so the net force on the block is upward.
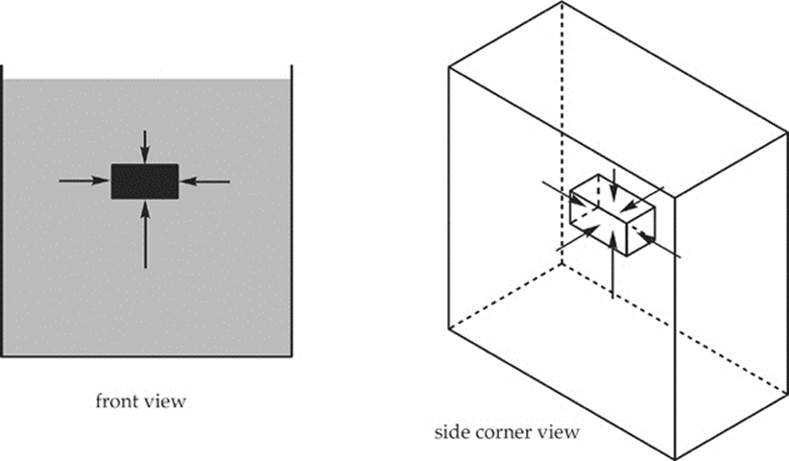
This net upward force is called the buoyant force (or just buoyancy for short), denoted Fbuoy. We calculate the magnitude of the buoyant force using Archimedes” principle; in words, Archimedes” principle says
The strength of the buoyant force is equal to the weight of the fluid displaced by the object.
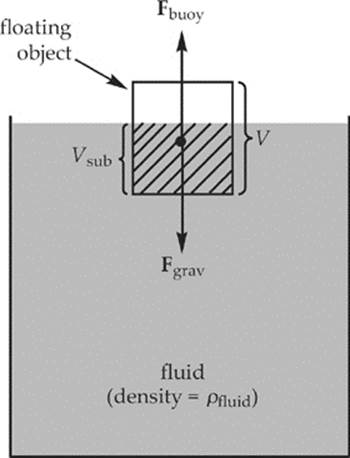
When an object is partially or completely submerged in a fluid, the volume of the object that”s submerged, which we call Vsub, is the volume of the fluid displaced. By multiplying this volume by the density of the fluid, we get the mass of the fluid displaced; then, multiplying this mass byg gives us the weight of the fluid displaced. So, here”s Archimedes” principle as a mathematical equation:
Buoyant force: Fbuoy = ρfluid Vsubg
When an object floats, its submerged volume is just enough to make the buoyant force it feels balance its weight. So, if an object”s density is ρobject and its (total) volume is V, its weight will be mg = ρVg. The buoyant force it feels is ρfluidVsub g. Setting these equal to each other, we find that
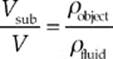
So, if ρobject < ρfluid, then the object will float; and the fraction of its volume that”s submerged is the same as the ratio of its density to the fluid”s density. For example, if the object”s density is 2/3 the density of the fluid, then the object will float, and 2/3 of the object will be submerged.
If an object is denser than the fluid, it will sink. In this case, even if the entire object is submerged (in an attempt to maximize Vsub and the buoyant force), its weight is still greater than the buoyant force, and down it goes. And if an object just happens to have the same density as the fluid, it will be happy hovering (in static equilibrium) anywhere underneath the fluid.
Example 8.9 An object with a mass of 150 kg and a volume of 0.75 m3 is floating in ethyl alcohol, whose specific gravity is 0.8. What fraction of the object”s volume is above the surface of the fluid?
Solution. The density of the object is
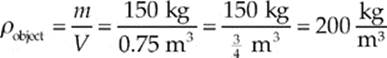
Because the density of the fluid is (sp. gr.)(ρwater) = (0.8)(1000![]() ) = 800
) = 800![]() , the ratio of the object”s density to the fluid”s density is
, the ratio of the object”s density to the fluid”s density is
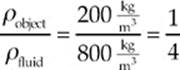
This means that 1/4 of the object”s volume is below the surface of the fluid; therefore, the fraction that”s above the surface is 1 – (1/4) = 3/4.
Example 8.10 A brick, of specific gravity 2 and volume 1.5 × 10–3 m3, is dropped into a swimming pool full of water.
(a) Explain briefly why the brick will sink.
(b) When the brick is lying on the bottom of the pool, what is the magnitude of the normal force on the brick?
Solution.
(a) Since the specific gravity of the brick is greater than 1, the brick has a greater density than the surrounding fluid (water), so it will sink.
(b) When the brick is lying on the bottom surface of the pool, it is totally submerged, so Vsub = V; this means the buoyant force on the brick is
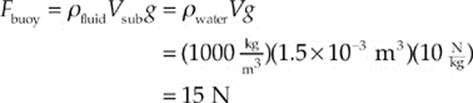
The weight of the brick is
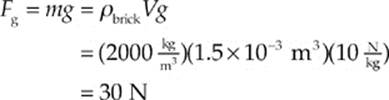
When the brick is lying on the bottom of the pool, the net force it feels is zero.
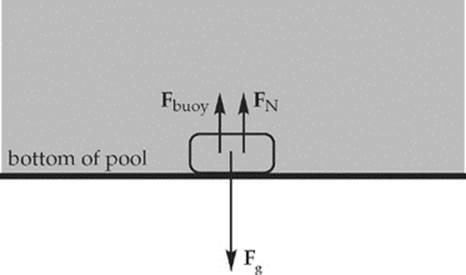
Therefore, we must have Fbuoy + FN = Fg, so FN = Fg – Fbuoy = 30 N – 15 N = 15 N.
Example 8.11 A glass sphere of specific gravity 2.5 and volume 10–3 m3 is completely submerged in a large container of water. What is the apparent weight of the sphere while immersed?
Solution. Because the buoyant force pushes up on the object, the object”s apparent weight, Fg apparent = Fg – Fbuoy, is less than its true weight, F. Since the sphere is completely submerged, we have Vsub = V, so the buoyant force on the sphere is
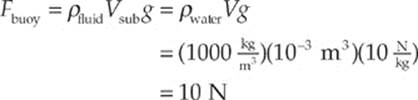
The true weight of the glass sphere is
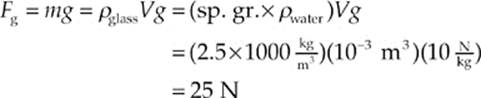
Therefore, the apparent weight of the sphere while immersed is
Fg apparent = Fg – Fbuoy = 25 N – 10 N = 15 N
Example 8.12 A helium balloon has a volume of 0.03 m3. What is the net force on the balloon if it”s surrounded by air? (Note: The density of helium is 0.2 kg/m3, and the density of air is 1.2 kg/m3.)
Solution. The balloon will feel a buoyant force upward, and the force of gravity—the balloon”s weight—downward. Because the balloon is completely surrounded by air, Vsub = V, and the buoyant force is
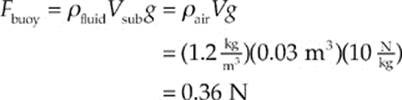
The weight of the balloon is
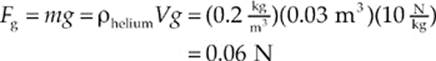
Because Fbuoy > w, the net force on the balloon is upward and has magnitude
Fnet = Fbuoy – Fg = 0.36 N – 0.06 N = 0.3 N
FLOW RATE AND THE CONTINUITY EQUATION
Consider a pipe through which fluid is flowing. The flow rate, f, is the volume of fluid that passes a particular point per unit time; for example, the number of liters of water per minute that are coming out of a faucet. In SI units, flow rate is expressed in m3/s. To find the flow rate, all we need to do is multiply the cross-sectional area of the pipe at any point by the average speed of the flow at that point.
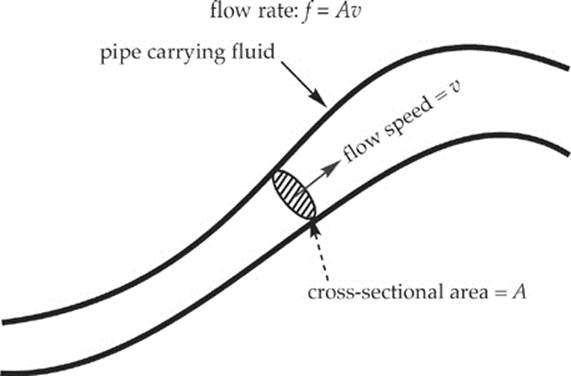
Be careful not to confuse flow rate with flow speed; flow rate tells us how much fluid flows per unit time; flow speed tells us how fast it”s moving.
If the pipe is carrying a liquid—which we assume is incompressible (that is, its density remains constant)—then the flow rate must be the same everywhere along the pipe. Choose any two points, Point 1 and Point 2, in a pipe carrying a liquid. If there aren”t any sources or sinks between these points, all the liquid that flows by Point 1 must also flow by Point 2. In other words, the flow rate at Point 1 must be the same as the flow rate at Point 2: f1 = f2. Rewriting this using f = Av, we get the Continuity Equation:
A1v1 = A2v2
Because the product Av is a constant, the flow speed will increase where the pipe narrows, and decrease where the pipe widens. In fact, we can say that the flow speed is inversely proportional to the cross-sectional area—or to the square of the radius—of the pipe.
Example 8.13 A pipe of non-uniform diameter carries water. At one point in the pipe, the radius is 2 cm and the flow speed is 6 m/s.
(a) What is the flow rate?
(b) What is the flow speed at a point where the pipe constricts to a radius of 1 cm?
Solution.
(a) At any point, the flow rate, f, is equal to the cross-sectional area of the pipe multiplied by the flow speed
![]()
(b) By the Continuity Equation, we know that v, the flow speed, is inversely proportional to A, the cross-sectional area of the pipe. If the pipe”s radius decreases by a factor of 2 (from 2 cm to 1 cm), then A decreases by a factor of 4, because A is proportional to r2. If A decreases by a factor of 4, then v will increase by a factor of 4. Therefore, the flow speed at a point where the pipe”s radius is 1 cm will be 4 × (6 m/s) = 24 m/s.
Example 8.14 If the diameter of a pipe increases from 4 cm to 12 cm, what will happen to the flow speed?
Solution. The cross-sectional area of the pipe is proportional not only to the square of the radius (r), but also to the square of the diameter (d), since A = πr2 = π(![]() d)2 =
d)2 = ![]() πd2. So, if d increases by a factor of 3, you can say the flow speed will decrease by a factor of 32 = 9 or you will have
πd2. So, if d increases by a factor of 3, you can say the flow speed will decrease by a factor of 32 = 9 or you will have ![]() of the flow rate.
of the flow rate.
BERNOULLI”S EQUATION
The most important equation in fluid mechanics is Bernoulli”s Equation, which is the statement of conservation of energy for ideal fluid flow. First, let”s describe the conditions that make fluid flow ideal.
· The fluid is incompressible.
This works very well for liquids and also applies to gases if the pressure changes are small.
· The fluid”s viscosity is negligible.
Viscosity is the force of cohesion between molecules in a fluid; think of viscosity as internal friction for fluids. For example, maple syrup is sticky and has a greater viscosity than water: there”s more resistance to a flow of maple syrup than to a flow of water. While Bernoulli”s Equation would give good results when applied to a flow of water, it would not give good results if it were applied to a flow of maple syrup.
· The flow is streamline.
In a tube carrying a flowing fluid, a streamline is just what it sounds like: it”s a line in the stream. If we were to inject a drop of dye into a clear glass pipe carrying, say, water, we”d see a streak of dye in the pipe, indicating a streamline.
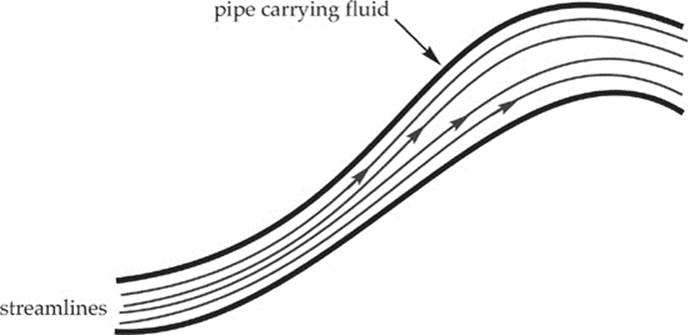
The entire flow is said to be streamline (as an adjective) or laminar if the individual streamlines don”t curl up into vortices but instead remain steady and smooth. When the flow is streamline, the fluid moves smoothly through the tube. (The opposite of streamline flow is turbulent flow, which is characterized by rapidly swirling whirlpools; such chaotic flow is unpredictable.)
If the three conditions described above hold, and the flow rate, f, is steady, Bernoulli”s Equation can be applied to any pair of points along a streamline within the flow. Let ρ be the density of the fluid that”s flowing. Label the points we want to compare as Point 1 and Point 2. Choose a horizontal reference level, and let y1 and y2 be the heights of these points above this level. If the pressures at Points 1 and 2 are P1 and P2, and if the flow speeds at these points are v1 and v2, then Bernoulli”s Equation says
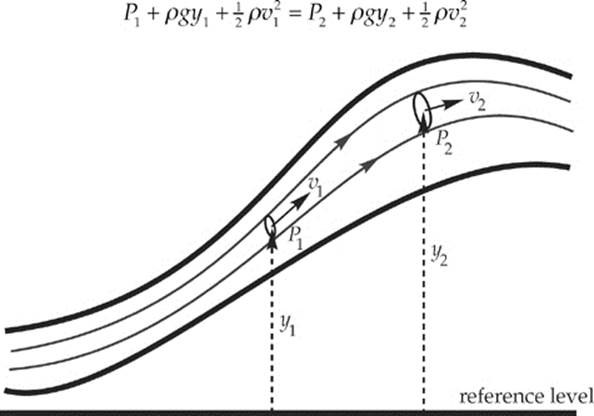
An alternative, but equivalent, way of stating Bernoulli”s Equation is to say that the quantity
![]()
is constant along a streamline. We mentioned earlier that Bernoulli”s Equation is a statement of conversation of energy. You should notice the similarity between ρgy and mgh (gravitational potential energy) as well as between ![]() ρv2 and
ρv2 and ![]() mv2 (kinetic energy).
mv2 (kinetic energy).
TORRICELLI”S THEOREM
Imagine that we punch a small hole in the side of a tank of liquid. We can use Bernoulli”s Equation to figure out the efflux speed: how fast the liquid will flow out of the hole.
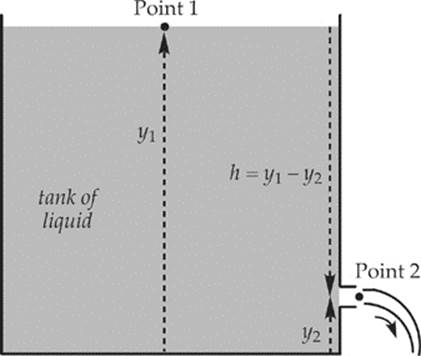
Let the bottom of the tank be our horizontal reference level, and choose Point 1 to be at the surface of the liquid and Point 2 to be at the hole where the water shoots out. First, the pressure at Point 1 is atmospheric pressure; and the emerging stream at Point 2 is open to the air, so it”s at atmospheric pressure too. Therefore, P1 = P2, and these terms cancel out of Bernoulli”s Equation. Next, since the area at Point 1 is so much greater than at Point 2, we can assume that v1, the speed at which the water level in the tank drops, is much lower than v2, the speed at which the water shoots out of the hole. (Remember that by the Continuity Equation, A1v1 = A2v2; since A1 >> A2, we”ll have v1 << v2.) Because v1 << v2, we can say that v1 ≈ 0 and ignore v1 in this case. So, Bernoulli”s Equation becomes
![]()
Solving for v2, we get
![]()
This is called Torricelli”s theorem. This result should look familiar; it”s the same formula that tells us how fast an object is going after it has fallen a distance h from rest.
Example 8.15 In the figure below, a pump forces water at a constant flow rate through a pipe whose cross-sectional area, A, gradually decreases: at the exit point, A has decreased to 1/3 its value at the beginning of the pipe. If y = 60 cm and the flow speed of the water just after it leaves the pump (Point 1 in the figure) is 1 m/s, what is the gauge pressure at Point 1?

Solution. We”ll apply Bernoulli”s Equation to Point 1 and the exit point, Point 2. We”ll choose the level of Point 1 as the horizontal reference level; this makes y1 = 0. Now, because the cross-sectional area of the pipe decreases by a factor of 3 between Points 1 and 2, the flow speed must increase by a factor of 3; that is, v2 = 3v1. Since the pressure at Point 2 is patm, Bernoulli”s Equation becomes
![]()
Therefore,
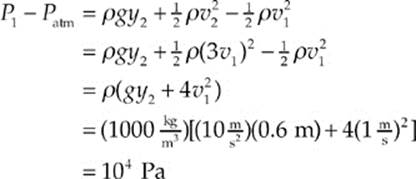
Example 8.16 What does Bernoulli”s Equation tell us about a fluid at rest in a container open to the atmosphere?
Solution. Consider the figure below:
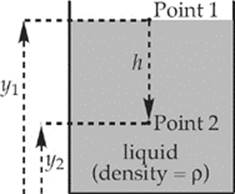
Because the fluid in the tank is at rest, both v1 and v2 are zero, and Bernoulli”s Equation becomes
P1 + ρgy1 = P2 + ρgy2
Since P1 = Patm, if we solve this equation for P2, we get
P2 = Patm + ρg(y1 − y2) = Patm + ρgh
which is the same formula we found earlier for hydrostatic pressure.
Example 8.17 The side of an above-ground pool is punctured, and water gushes out through the hole. If the total depth of the pool is 2.5 m, and the puncture is 1 m above ground level, what is the efflux speed of the water?
Solution. Torricelli”s Theorem is v = ![]() , where h is the distance from the surface of the pool down to the hole. If the puncture is 1 m above ground level, then it”s 2.5 – 1 = 1.5 m below the surface of the water (because the pool is 2.5 m deep). Therefore, the efflux speed will be
, where h is the distance from the surface of the pool down to the hole. If the puncture is 1 m above ground level, then it”s 2.5 – 1 = 1.5 m below the surface of the water (because the pool is 2.5 m deep). Therefore, the efflux speed will be
![]()
THE BERNOULLI EFFECT
Consider the two points labeled in the pipe shown below:
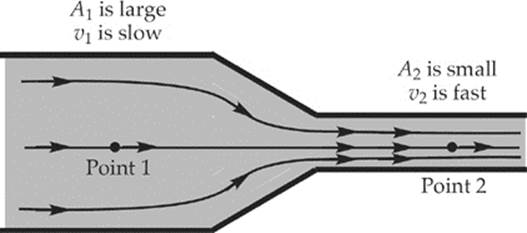
Since the heights y1 and y2 are equal in this case, the terms in Bernoulli”s Equation that involve the heights will cancel, leaving us with
![]()
We already know from the Continuity Equation (f = Av) that the speed increases as the cross-sectional area of the pipe decreases; that is, since A2 < A1, we know that v2 > v1, so the equation above tells us that P2 < P1. This shows that
The pressure is lower where the flow speed is greater.
This is known as the Bernoulli (or Venturi) effect, and is illustrated in the figure below.
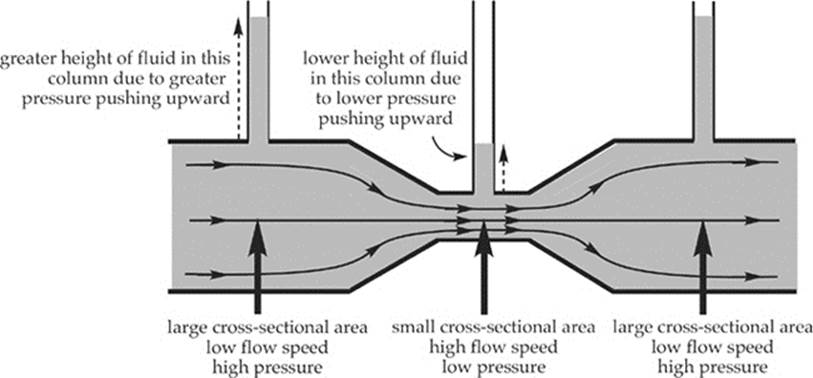
The height of the liquid column above Point 2 is less than the height of the liquid column above Point 1, because the pressure at Point 2 is lower than at Point 1, due to the fact that the flow speed at Point 2 is greater than at Point 1.
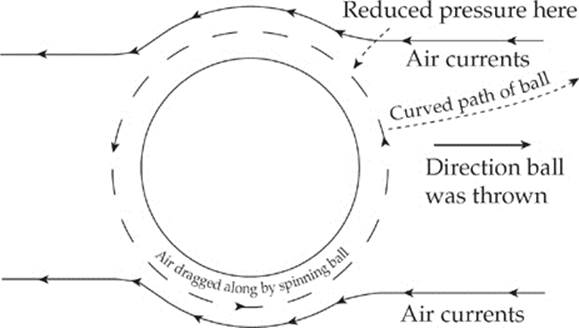
The Bernoulli Effect also accounts for many everyday phenomena. It”s what allows airplanes to fly, curve balls to curve, and tennis balls hit with top spin to drop quickly. You may have seen sky divers or motorcycle riders wearing a jacket that seems to puff out as they move rapidly through the air. The essentially stagnant air trapped inside the jacket is at a much higher pressure than the air whizzing by outside, and as a result, the jacket expands outward. The drastic drop in air pressure that accompanies the high winds in a hurricane or tornado is yet another example. In fact, if high winds streak across the roof of a house whose windows are closed, the outside air pressure can be reduced so much that the air pressure inside the house (where the air speed is essentially zero) can be great enough to blow the roof off.
CHAPTER 8 REVIEW QUESTIONS
Solutions can be found in Chapter 18.
SECTION I: MULTIPLE CHOICE
1. A large tank is filled with water to a depth of 6 m. If Point X is 1 m from the bottom and Point Y is 2 m from the bottom, how does pX, the hydrostatic pressure due to the water at Point X, compare to pY, the hydrostatic pressure due to the water at Point Y?
(A) pX = 2pY
(B) 2pX = pY
(C) 5pX = 4pY
(D) 4pX = 5pY
(E) pX = 4pY
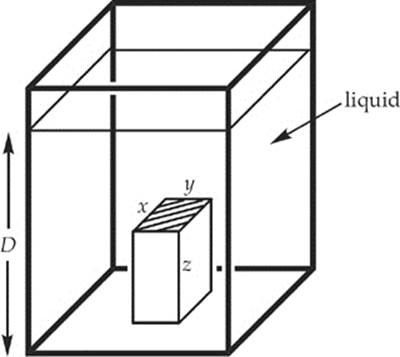
2. In the figure above, a box of dimensions x, y, and z rests on the bottom of a tank filled to depth D with a liquid of density ρ. If the tank is open to the atmosphere, what is the force on the (shaded) top of the box?
(A) xy(patm + ρgD)
(B) xyz[patm − ρg(z − D)]
(C) xy[patm + ρg(D − z)]
(D) xyz[patm + ρgD]
(E) xy(patm + ρgz)

3. The figure above shows a closed container partially filled with liquid. Point Y is at a depth of 1 m, and Point Z is at a depth of 3 m. If the absolute pressure at Point Y is 13,000 Pa, and the absolute pressure at Point Z is 29,000 Pa, what is the pressure at the surface, Point X?
(A) 3,000 Pa
(B) 4,000 Pa
(C) 5,000 Pa
(D) 7,000 Pa
(E) 8,000 Pa
4. A plastic cube 0.5 m on each side and with a mass of 100 kg floats in water. What fraction of the cube”s volume is above the surface of the water?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
5. A block of Styrofoam, with a density of ρS and volume V, is pushed completely beneath the surface of a liquid whose density is ρL, and released from rest. Given that ρL > ρS, which of the following expressions gives the magnitude of the block”s initial upward acceleration?
(A) (ρL − ρS)g
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
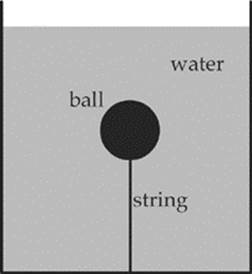
6. In the figure above, a ball of specific gravity 0.4 and volume 5 × 10–3 m3 is attached to a string, the other end of which is fastened to the bottom of the tank. If the tank is filled with water, what is the tension in the string?
(A) 20 N
(B) 30 N
(C) 40 N
(D) 50 N
(E) 70 N
7. An object of specific gravity 2 weighs 100 N less when it”s weighed while completely submerged in water than when it”s weighed in air. What is the actual weight of this object?
(A) 200 N
(B) 300 N
(C) 400 N
(D) 600 N
(E) 800 N
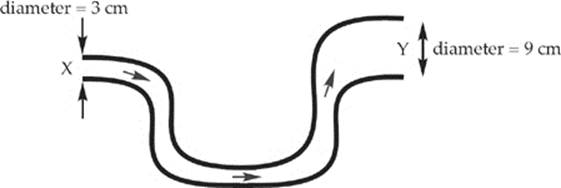
8. In the pipe shown above, which carries water, the flow speed at Point X is 6 m/s. What is the flow speed at Point Y?
(A) ![]() m/s
m/s
(B) 2 m/s
(C) 4 m/s
(D) 18 m/s
(E) 54 m/s
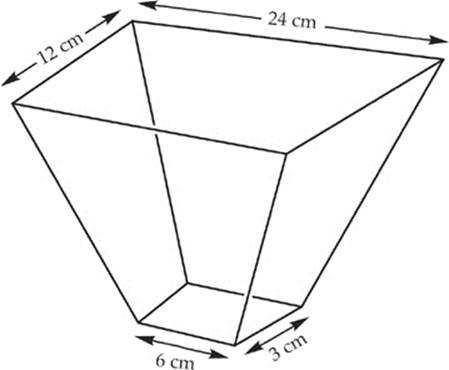
9. The figure above shows a portion of a conduit for water, one with rectangular cross sections. If the flow speed at the top is v, what is the flow speed at the bottom?
(A) 2v
(B) 4v
(C) 8v
(D) 12v
(E) 16v
10. A pump is used to send water through a hose, the diameter of which is 10 times that of the nozzle through which the water exits. If the nozzle is 1 m higher than the pump, and the water flows through the hose at 0.4 m/s, what is the gauge pressure of the water at the pump?
(A) 108 kPa
(B) 260 kPa
(C) 400 kPa
(D) 810 kPa
(E) 1080 kPa
SECTION II: FREE RESPONSE
1. The figure below shows a tank open to the atmosphere and filled to depth D with a liquid of density ρL. Suspended from a string is a block of density ρB (which is greater than ρL), whose dimensions are x, y, and z (meters). The top of the block is at depth h meters below the surface of the liquid.
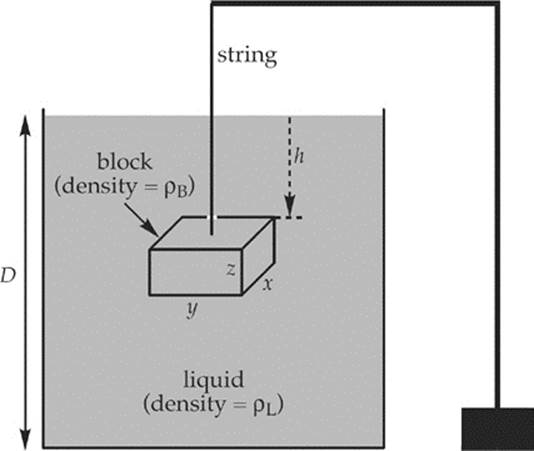
In each of the following, write your answer in simplest form in terms of ρL, ρB, x, y, z, h, D, and g.
(a) Find the force due to the pressure on the top surface of the block and on the bottom surface. Sketch these forces in the diagram below:
(b) What are the average forces due to the pressure on the other four sides of the block? Sketch these forces in the diagram above.
(c) What is the total force on the block due to the pressure?
(d) Find an expression for the buoyant force on the block. How does your answer here compare to your answer to part (c)?
(e) What is the tension in the string?
2. The figure below shows a large, cylindrical tank of water, open to the atmosphere, filled with water to depth D. The radius of the tank is R. At a depth h below the surface, a small circular hole of radius r is punctured in the side of the tank, and the point where the emerging stream strikes the level ground is labeled X.
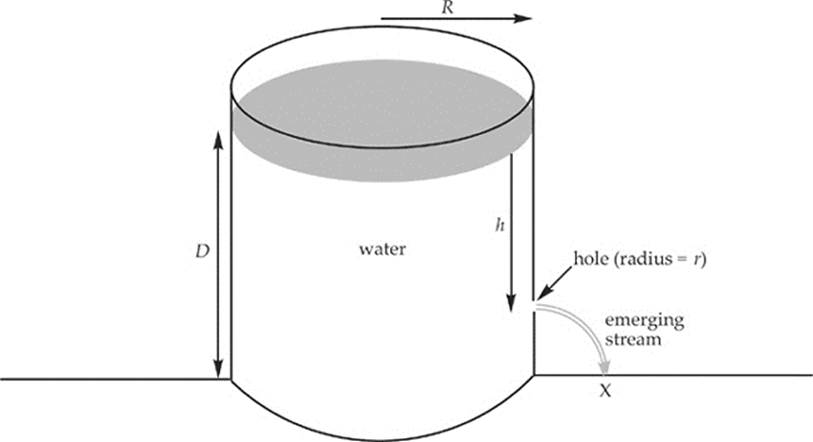
In parts (a) through (c), assume that the speed with which the water level in the tank drops is negligible.
(a) At what speed does the water emerge from the hole?
(b) How far is point X from the edge of the tank?
(c) Assume that a second small hole is punctured in the side of the tank, a distance of h/2 directly above the hole shown in the figure. If the stream of water emerging from this second hole also lands at Point X, find h in terms of D.
(d) For this part, do not assume that the speed with which the water level in the tank drops is negligible, and derive an expression for the speed of efflux from the hole punctured at depth h below the surface of the water. Write your answer in terms of r, R, h, and g.
3. The figure below shows a pipe fitted with a Venturi U-tube. Fluid of density ρF flows at a constant flow rate and with negligible viscosity through the pipe, which constricts from a cross-sectional area A1 at Point 1 to a smaller cross-sectional area A2 at Point 2. The upper portion of both sides of the Venturi U-tube contain the same fluid that”s flowing through the pipe, while the lower portion is filled with a fluid of density ρV (which is greater than ρF). At Point 1 in the pipe, the pressure is P1 and the flow speed is v1; at Point 2 in the pipe, the pressure is P2 and the flow speed is v2. All the fluid within the Venturi U-tube is stationary.
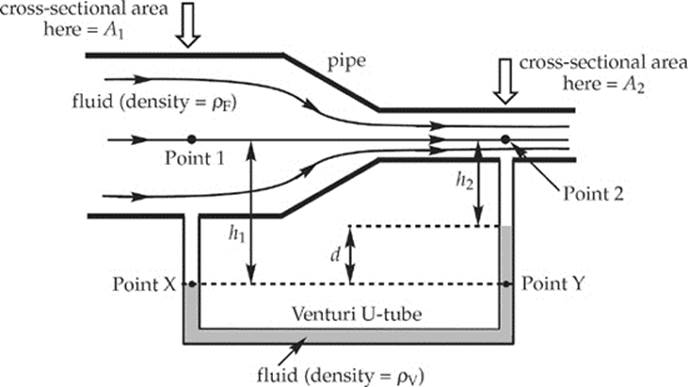
(a) What is PX, the hydrostatic pressure at Point X? Write your answer in terms of P1, ρF, h1, and g.
(b) What is PY, the hydrostatic pressure at Point Y? Write your answer in terms of P2, ρF, ρV, h2, d, and g.
(c) Write down the result of Bernoulli”s Equation applied to Points 1 and 2 in the pipe, and solve for P1 – P2.
(d) Since PX = PY, set the expressions you derived in parts (a) and (b) equal to each other, and use this equation to find P1 – P2.
(e) Derive an expression for the flow speed, v2, and the flow rate, f, in terms of A1, A2, d, ρF, ρV, and g. Show that v2 and f are proportional to ![]() .
.
SUMMARY
· Density is given by ρ = ![]() . Pressure is given by P =
. Pressure is given by P = ![]() . Hydrostatic pressure can be found using P = P0 + ρgh where ρgh is the pressure at a given depth below the surface of the fluid and P0 is the pressure right above the surface of the fluid.
. Hydrostatic pressure can be found using P = P0 + ρgh where ρgh is the pressure at a given depth below the surface of the fluid and P0 is the pressure right above the surface of the fluid.
· The buoyant force is an upward force any object immersed in a fluid experiences due to the displaced fluid. The buoyant force is given by Fbuoy = ρVg, where V is the volume of the fluid displaced.
· The Continuity Equation says that the flow rate through a pipe (area times velocity) is constant so that A1v1 = A2v2. This expresses the idea that a larger cross sectional area of pipe will experience fluids traveling at a lower velocity.
· Bernoulli”s Equation is a statement of conservation of energy. It states