AP Physics B Exam
9 Thermal Physics
INTRODUCTION
This chapter looks at heat and temperature, concepts that seem familiar from our everyday experience. Technically, heat is defined as thermal energy that”s transmitted from one body to another. While an object can contain thermal energy (due to the random motion of its molecules), an object doesn”t contain heat; heat is energy that”s in transit. Temperature, on the other hand, is a measure of the concentration of an object”s internal thermal energy, and is one of the basic SI units.
TEMPERATURE SCALES
In the United States, temperatures are still often expressed in degrees Fahrenheit (°F). On this scale, water freezes at 32°F and boils at 212°F. In other countries, temperature is expressed in degrees Celsius (°C); water freezes at 0°C and boils at 100°C. The size of a Fahrenheit degree is smaller than a Celsius degree, and the conversion between these two scales is given by the formula
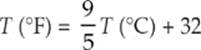
The Celsius scale is sometimes used in scientific work, but it”s giving way to the absolute temperature scale, in which temperatures are expressed in kelvins (K). On the Kelvin scale, water freezes at 273.15 K and boils at 373.15 K. Notice that the degree sign is not used for absolute temperature. The Kelvin scale assigns a value of 0 K to the lowest theoretically possible temperature and a value of 273.16 K to the triple point of water (the temperature at which the three phases of water—liquid water, ice, and vapor—can coexist when the pressure is one atmosphere). A kelvin is equal in size to a Celsius degree, and the conversion between kelvins and degrees Celsius is
T(K) = T (°C) + 273.15
For most purposes, you can ignore the .15 and use the simpler conversion equation T = T (°C) + 273.
Example 9.1 Room temperature is 68°F. What”s this temperature in kelvins?
Solution. Let”s convert this to Celsius. Since T (°F) = ![]() T (°C) + 32, it”s also true that T (°C) =
T (°C) + 32, it”s also true that T (°C) = ![]() (T (°F) – 32), so 68°F is equal to
(T (°F) – 32), so 68°F is equal to ![]() (68 – 32) = 20°C. Converting this to kelvins, we add 273; room temperature is 293 K.
(68 – 32) = 20°C. Converting this to kelvins, we add 273; room temperature is 293 K.
PHYSICAL CHANGES DUE TO HEAT TRANSFER
When a substance absorbs or gives off heat, one of two things can happen:
(1) the temperature of the substance can change
(2) the substance can undergo a phase change
There are three phases of matter: solid, liquid, and vapor (or gas). When a solid melts (or liquefies), it becomes a liquid; the reverse process occurs when a liquid freezes (or solidifies) to become a solid. A liquid can evaporate (to become vapor), and vapor can condense to become liquid. These are the most common phase changes, but others exist: A solid can sublimate, going directly to vapor form, and vapor can experience deposition, going directly to solid.
Since either change (1) or change (2)—but not both—takes place upon heat transfer, let”s study these changes separately.
CALORIMETRY I: HEAT TRANSFER AND TEMPERATURE CHANGE
The change in temperature that a substance experiences upon a transfer of heat depends upon two things: the identity and the amount of the substance present. For example, we could transfer 200 J of heat to a gold nugget and a piece of wood of equal mass and, even though they were infused with the same amount of thermal energy, the temperature of the gold would rise much more than the temperature of the wood. Also, if this heat were transferred to two nuggets of gold of unequal mass, the temperature of the smaller nugget would rise more than that of the bigger one. The equation that connects the amount of heat, Q, and the resulting temperature change, ∆T, is
Q = mc∆T
where m is the mass of the sample and c is an intrinsic property of the substance called its specific heat. Notice that positive Q is interpreted as heat coming in (∆T is positive, so T increases), while negative Q corresponds to heat going out (∆T is negative, so T decreases).
CALORIMETRY II: HEAT TRANSFER AND PHASE CHANGES
Consider an ice cube. Since water freezes at 0°C, the temperature of the ice cube is 0°C. If we add heat to the ice, its temperature does not rise. Instead, the thermal energy absorbed by the ice goes into loosening the intermolecular bonds of the solid, thereby transforming it into liquid. The temperature remains at 0°C throughout this melting process. Once the ice cube is completely melted, additional heat will increase the temperature of the liquid, until it reaches its boiling point temperature (100°C). At this point, additional heat does not increase the temperature; it breaks the intermolecular bonds, transforming it into steam. In each of the phase changes (solid to liquid, liquid to vapor), absorbed heat causes no temperature change, so Q = mc∆T does not apply at these transitions. The equation that does apply is
Q = mL
where L is the latent heat of transformation. This equation tells us how much heat must be transferred in order to cause a sample of mass m to completely undergo a phase change. In the case of a solid to liquid (or vice versa) phase change, L is called the latent heat of fusion. For a phase change between liquid and vapor, L is called the latent heat of vaporization.
THERMAL EXPANSION
When a substance undergoes a temperature change, it changes in size. Steel beams that form railroad tracks or bridges expand when they get warmer; a balloon filled with air shrinks when it”s placed in a freezer. The change in size of a substance due to a temperature change depends on the amount of the temperature change and the identity of the substance.
Let”s first consider changes in length (of the steel beam, for example). When its temperature is Ti, its length is ![]() i. Then, if its temperature changes to Tf, the length changes to
i. Then, if its temperature changes to Tf, the length changes to ![]() f, such that
f, such that
![]() f –
f – ![]() i = αLi(Tf – Ti)
i = αLi(Tf – Ti)
where α is the coefficient of linear expansion of the material. This equation is usually used in the simpler form
∆![]() = α
= α![]() o ∆T
o ∆T
Nearly all substances have a positive value of α, which means they expand upon heating.
Example 9.2 A brass rod 5 m long and 0.01 m in diameter increases in length by 0.05 m when its temperature is increased by 500°C. A similar brass rod of length 10 m has a diameter of 0.02 m. By how much will this rod”s diameter increase if its temperature is increased by 1000°C?
Solution. First, let”s use the equation Δ![]() = α
= α![]() iΔT to determine α, the coefficient of linear expansion of the brass rod
iΔT to determine α, the coefficient of linear expansion of the brass rod
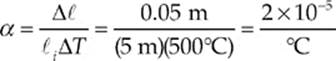
Like length, the diameter is also a linear dimension, so we now use this value of α in the same equation to determine the increase in diameter of the second brass rod. With ![]() i now denoting the initial diameter of the second brass rod, we find that
i now denoting the initial diameter of the second brass rod, we find that
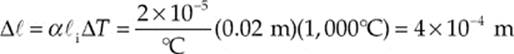
As we”ve mentioned, substances also undergo volume changes when heat is lost or absorbed. The change in volume, ∆V, corresponding to a temperature change ∆T is given by the equation
∆V = βVi∆T
where Vi is the sample”s initial volume and β is the coefficient of volume expansion of the substance. Since we”re now looking at the change in a three-dimensional quantity (volume) rather than a one-dimensional quantity (length), for most solids, β ≈ 3α. Nearly all substances have a positive value of β, which means that they expand upon heating. An extremely important example of a substance with a negative value of β is liquid water between 0°C and 4°C. Unlike the vast majority of substances, liquid water expands as it nears its freezing point and solidifies (which is why ice has a lower density and floats in water).
HEAT TRANSFER
Heat conducts from one point to another only if there is a temperature difference between the two objects. The rate at which heat is transferred is given by 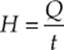 or
or ![]() where k is the thermal conductivity (a property of the material), A is the cross-sectional area, ∆T is the temperature difference between the two sides and L is the thickness or distance between the two ends of the material.
where k is the thermal conductivity (a property of the material), A is the cross-sectional area, ∆T is the temperature difference between the two sides and L is the thickness or distance between the two ends of the material.
Example 9.3 An aluminum rod (ρ = 2.7 × 103 kg/m3) has a radius of 0.01 m and an initial length of 2 m at a temperature of 20°C. Heat is added to raise its temperature to 90°C. Its coefficient of linear expansion is α = 25 × 10–6/°C, the specific heat is cal = 900 J/kg°C, and a thermal conductivity of k = 200 J/s·m°C.
(a) What is the mass of the aluminum rod?
(b) What is the amount of heat added to the rod?
(c) What is the new length of the rod?
(d) If we were to use this rod to transfer heat between two objects one side being at 20°C and the other side at 90°C, what would the rate of heat transfer be?
Solution.
(a) Because ρ = m/V we know m = ρV. The term rod implies a long cylinder and the volume of a cylinder is given by V = πr2h. Therefore:
![]()
This becomes
![]()
or
![]()
(b) Given ∆Q = mc∆T we can now substitute in
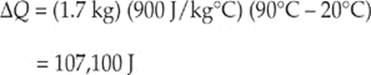
(c) The new length of the rod can be given by
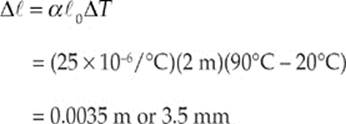
Therefore the new length is given by
![]()
Or ![]() = 2.0035 m
= 2.0035 m
(d) We know that H = 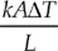 and the cross-sectional area of a cylinder is A = πr2 so
and the cross-sectional area of a cylinder is A = πr2 so
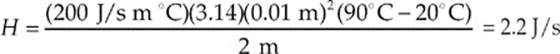
THE KINETIC THEORY OF GASES
Unlike the condensed phases of matter—solid and liquid—the atoms or molecules that make up a gas do not move around relatively fixed positions. Rather, the molecules of a gas move freely and rapidly, in a chaotic swarm.
A confined gas exerts a force on the walls of its container, because the molecules are zipping around inside the container, striking the walls and rebounding. The magnitude of the force per unit area is called pressure, and is denoted by P
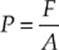
The SI unit for pressure is the N/m2, the pascal (abbreviated Pa). As we”ll see, the faster the gas molecules are moving, the more pressure they exert.
We also need a way to talk about the typically vast numbers of molecules in a given sample of gas. We will say N = nNA where N is the number of molecules, n is a mole, and
NA = 6.022 × 1023 molecules/mole
The number NA is known as Avogadro”s constant, and one mole of any substance has a mass in grams that defines its atomic or molecular mass (these values are given in the Periodic Table of Elements). For example, the mass of a carbon-12 atom (the most abundant isotope of carbon) has a mass of exactly 12 atomic mass units, and a mole of these atoms has a mass of 12 grams. Oxygen has an atomic mass of 16 g, so a mole of carbon dioxide (CO2), each molecule of which is composed of one carbon atom and two oxygen atoms, has a mass of 12 g + 2(16 g) = 44 g.
THE IDEAL GAS LAW
Three physical properties—pressure (P), volume (V), and temperature (T)—describe a gas. At low densities, all gases approach ideal behavior; this means that these three variables are related by the equation
PV = nRT
where n is the number of moles of gas and R is a constant (8.31 J/mol·K) called the universal gas constant. This equation is known as the Ideal Gas Law. It can also be written as PV = NkBT, where kB is Boltzmann”s constant (KB = 1.38 × 10–23 J/K).
An important consequence of this equation is that, for a fixed volume of gas, an increase in P gives a proportional increase in T. The pressure increases when the gas molecules strike the walls of their container with more force, which occurs if they move more rapidly. Using Newton”s Second Law (rate of change of momentum = force) we can find that the pressure exerted by N molecules of gas in a container of volume V is related to the average kinetic energy of the molecules by the equation PV = NKavg. Comparing this to the Ideal Gas Law we see that ![]() NKavg = nRT. We can rewrite this equation in the form
NKavg = nRT. We can rewrite this equation in the form ![]() NAKavg = RT, since, by definition, N = nNA. The ratio R/NA is a fundamental constant of nature called Boltzmann”s constant (kB = 1.38 × 10–23 J/K), so our equation becomes
NAKavg = RT, since, by definition, N = nNA. The ratio R/NA is a fundamental constant of nature called Boltzmann”s constant (kB = 1.38 × 10–23 J/K), so our equation becomes
![]()
This tells us that the average translational kinetic energy of the gas molecules is directly proportional to the absolute temperature of the sample. Remember, this means you must use kelvins as your temperature unit.
Since the average kinetic energy of the gas molecules is Kavg = ![]() μ(v2)avg, where µ is the mass of each molecule, the equation above becomes
μ(v2)avg, where µ is the mass of each molecule, the equation above becomes ![]() μ(v2)avg =
μ(v2)avg = ![]() kBT, so
kBT, so

The quantity on the left-hand side of this equation, the square root of the average of the square of v, is called the root-mean-square speed, vrms, so
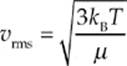
Because kB = R/NA and µNA = M (the mass of one mole of the molecules—the molar mass), the equation for vrms is also commonly written in the form
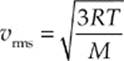
Note that these last two equations can only determine vrms. It”s important to realize that the molecules in the container have a wide range of speeds; some are much slower and others are much faster than vrms. The root-mean-square speed is important because it gives us a type of average speed that”s easy to calculate from the temperature of the gas.
Example 9.4 In order for the rms speed of the molecules in a given sample of gas to double, what must happen to the temperature?
Solution. Temperature is a measure of the average kinetic energy. The velocity is determined from the following equation:
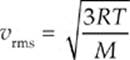
Since vrms is proportional to the square root of T, the temperature must quadruple, again, assuming the temperature is given in kelvins.
Example 9.5 Standard atmospheric pressure is 1.013 × 105 Pa (this is one atmosphere). At 0°C = 273.15 K, one mole of any ideal gas occupies the same volume. What is this volume?
Solution. Use the Ideal Gas Law:
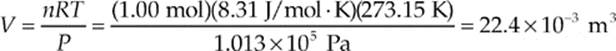
The quantity 10–3 m3 is the definition of a liter (L), so the volume occupied by any ideal gas at STP (standard temperature and pressure, 0°C and 1 atm) is 22.4 L.
Example 9.6 A 0.1-mole sample of gas is confined to a jar whose volume is 4.0 L. To what temperature must the gas be raised to cause the pressure of the gas to increase to 2 atm?
Solution. Use the Ideal Gas Law:
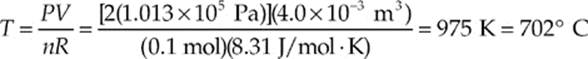
Example 9.7 A cylindrical container of radius 15 cm and height 30 cm contains 0.6 mole of gas at 433 K. How much force does the confined gas exert on the lid of the container?
Solution. The volume of the cylinder is πr2h, where r is the radius and h is the height. Since we know V and T, we can use the Ideal Gas Law to find P. Because pressure is force per unit area, we can find the force on the lid by multiplying the gas pressure times the area of the lid.
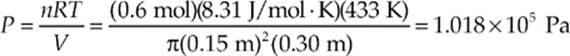
So, since the area of the lid is πr2, the force exerted by the confined gas on the lid is:
![]()
This is about 1600 pounds of force, which seems like a lot. Why doesn”t this pressure pop the lid off? Because, while the bottom of the lid is feeling a pressure (due to the confined gas) of 1.018 × 105 Pa that exerts a force upward, the top of the lid feels a pressure of 1.013 × 105 Pa (due to the atmosphere) that exerts a force downward. The net force on the lid is
![]()
which is only about 8 pounds.
THE LAWS OF THERMODYNAMICS
We”ve learned about two ways in which energy may be transferred between a system and its environment. One is work, which takes place when a force acts over a distance. The other is heat, which takes place when energy is transferred due to a difference in temperature. The study of the energy transfers involving work and heat, and the resulting changes in internal energy, temperature, volume, and pressure is called thermodynamics.
THE ZEROTH LAW OF THERMODYNAMICS
When two objects are brought into contact, heat will flow from the warmer object to the cooler one until they reach thermal equilibrium. This property of temperature is expressed by the Zeroth Law of Thermodynamics: If Objects 1 and 2 are each in thermal equilibrium with Object 3, then Objects 1 and 2 are in thermal equilibrium with each other.
Example 9.8 What is the final temperature of a mixture of 200 g of water that has an initial temperature of 20°C and 800 g of water that is initially at 60°C? Assume no heat lost to the environment.
Solution. For a closed system, ΣQ = 0. This means
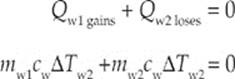
The specific heat of water is the same for both samples so this can be eliminated

Example 9.9 500 g of water has an initial temperature of 20°C. 200 g of steel (c = 0.11 J/g°C) is initially at 80°C and is placed in the water. Assuming no heat is lost to the environment, what is the final temperature of the mixture?
Solution. For a closed system, ΣQ = 0. This means

THE FIRST LAW OF THERMODYNAMICS
Simply put, the First Law of Thermodynamics is a statement of the Conservation of Energy that includes heat. Consider the following example, which is the prototype that”s studied extensively in thermodynamics.
An insulated container filled with an ideal gas rests on a heat reservoir (that is, something that can act as a heat source or a heat sink). The container is fitted with a snug, but frictionless, weighted piston that can be raised or lowered. The confined gas is the system, and the piston and heat reservoir are the surroundings.
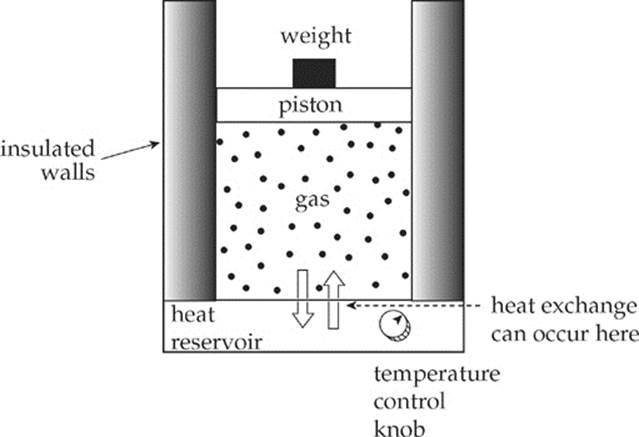
The state of the gas is given once its pressure, volume, and temperature are known, and the equation that connects these state variables is the Ideal Gas Law, PV = nRT. We”ll imagine performing different experiments with the gas, such as heating it or allowing it to cool, increasing or decreasing the weight on the piston, etc., and study the energy transfers (work and heat) and the changes in the state variables. If each process is carried out such that, at each moment, the system and its surroundings are in thermal equilibrium, we can plot the pressure (P) vs. the volume (V) on a diagram. By following the path of this P-V diagram, we can study how the system is affected as it moves from one state to another.
Work is done on or by the system when the piston is moved and the volume of the gas changes. For example, imagine that the weight pushes the piston downward a distance d, causing a decrease in volume. Assume that the pressure stays constant at P. (Heat must be removed via the reservoir to accomplish this.) We can calculate the work done on the gas during this compression as W = –Fd, but since F = PA, we have W = –PAd, and because Ad = ∆V, we have
W = –P∆V
Textbooks differ about the circumstances under which work in thermodynamics is defined to be positive or negative. The negative signs we have included in the equations above are consistent with those used in the AP Physics Exam (appearing in the equation sheet given for Section II). For the exam, work in thermodynamics is considered to be positive when the work is being done on the system. This means that the volume of the system is decreasing, ∆V is negative, and, in agreement with intuition, energy is being added to the system. In other words, when work is done in compressing a system, ∆V is negative and the work done, W = –P∆V, is positive. This also means, conversely, that when the system is doing work on the surroundings (volume increasing, ∆V positive), the work is negative, in agreement with intuition that energy is leaving the system.
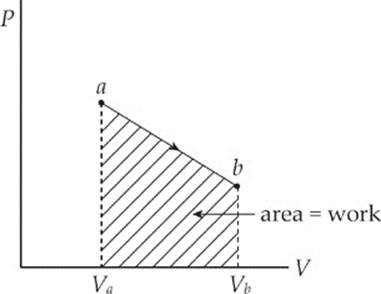
The equation W = –P∆V assumes that the pressure P does not change during the process. If P does change, then the work is equal to the area under the curve in the P–V diagram; moving left to right gives a negative area (and negative work), while moving right to left gives a positive area (and positive work).
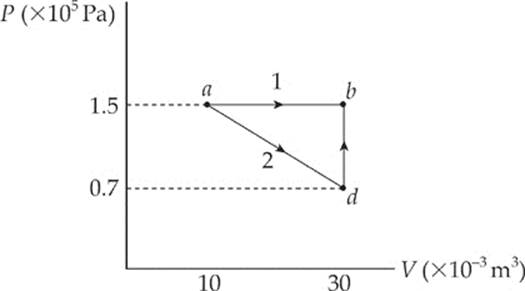
Example 9.10 What”s the value of W for the process ab following path 1 and for the same process following path 2 (from a to d to b), shown in the P–V diagram below?
Solution.
Path 1. Since, in path 1, P remains constant, the work done is just –P ∆ V:
W = –P∆V = – (1.5 × 105 Pa)[(30 × 10–3 m3) – (10 × 10–3 m3)] = –3,000 J
Path 2. If the gas is brought from state a to state b, along path 2, then work is done only along the part from a to d. From d to b, the volume of the gas does not change, so no work can be performed. The area under the graph from a to d is
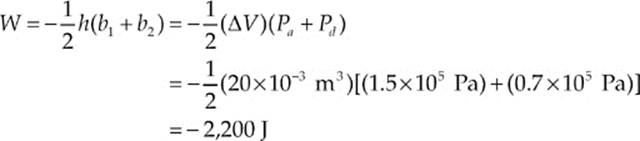
As this example shows, the value of W depends not only on the initial and final states of the system, but also on the path between the two. In general, different paths give different values for W.
Experiments have shown that the value of Q + W is not path dependent; it depends only on the initial and the final state of the system, so it describes a change in a fundamental property. This property is called the system”s internal energy, denoted U, and the change in the system”s internal energy, ∆U, is equal to Q + W. This is true regardless of the process that brought the system from its initial to final state. This statement is known as
The First Law of Thermodynamics
∆U = Q + W
∆U depends only on temperature change
(assuming no phase changes).
(If volume is constant, W = 0 and U = Q = nCv∆T.)
This statement of the First Law is consistent with the interpretation of work (W = –PΔV) explained above. The First Law identifies W and Q as separate physical mechanisms for adding to or removing energy from the system, and the signs of both W and Q are defined consistently: Both are positive when they are adding energy to the system and negative when they are removing energy from the system.
Example 9.11 A 0.5 mol sample of an ideal gas is brought from state a to state b when 7500 J of heat is added along the path shown in the following P–V diagram:
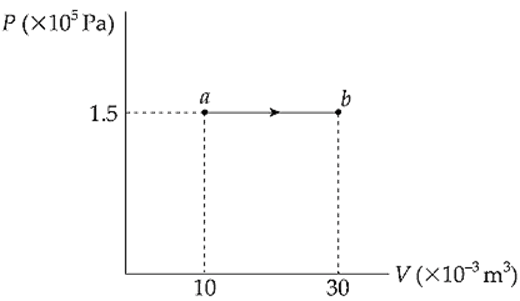
What are the values of each of the following?
(a) the temperature at a
(b) the temperature at b
(c) the work done by the gas during process ab
(d) the change in the internal energy of the gas
Solution.
(a, b) Both of these questions can be answered using the Ideal Gas Law, T = PV/(nR):
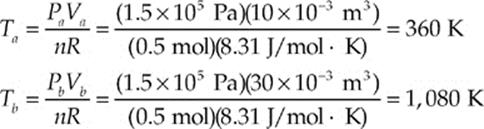
(c) Since the pressure remains constant during the process, we can use the equation W = –P∆V. Because ∆V = (30 – 10) × 10–3 m3 = 20 × 10–3 m3, we find that
W = –P∆V = (1.5 × 105 Pa)(20 × 10–3 m3) = –3000 J
The expanding gas did negative work against its surroundings, pushing the piston upward. [Important note: If the pressure remains constant (which is designated by a horizontal line in the P–V diagram), the process is called isobaric.]
(d) By the First Law of Thermodynamics,
∆U = Q + W = 7,500 – 3,000 J = 4,500 J
Example 9.12 A 0.5 mol sample of an ideal monatomic gas is brought from state a to state b along the path shown in the following P–V diagram:
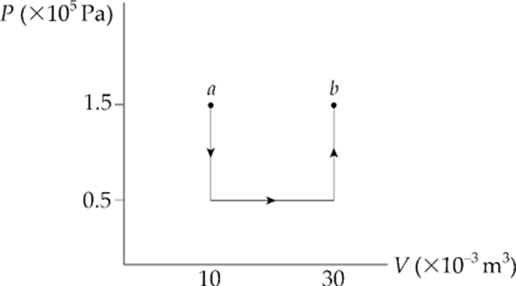
What are the values of each of the following?
(a) the work done by the gas during process ab
(b) the change in the internal energy of the gas
(c) the heat added to the gas during process ab
Solution. Note that the initial and final states of the gas are the same as in the preceding example, but the path is different.
(a) Let”s break the path into 3 pieces:
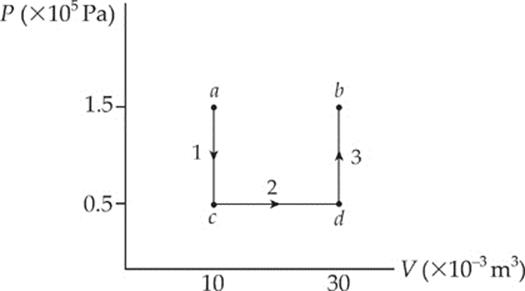
Over paths 1 and 3, the volume does not change, so no work is done. Work is done only over path 2:
W = –P∆V = –(0.5 × 105 Pa)(20 × 10–3 m3) = –1,000 J
Once again, the expanding gas does negative work against its surroundings, pushing the piston upward.
(b) Because the initial and final states of the gas are the same here as they were in the preceding example, the change in internal energy, ∆U, must be the same. Therefore, ∆U = 4500 J.
(c) By the First Law of Thermodynamics, ∆U = Q + W, so
Q = ∆U − W = 4,500J − (−1,000 J) = 5,500 J
Example 9.13 As isochoric process is one that takes place with no change in volume. What can you say about the change in the internal energy of a gas if it undergoes an isochoric change of state?
Solution. An isochoric process is illustrated by a vertical line in a P–V diagram and, since no change in volume occurs, W = 0. By the First Law of Thermodynamics, ∆U = Q + W = Q. Therefore, the change in internal energy is entirely due to (and equal to) the heat transferred. If heat is transferred into the system (positive Q), then ∆U is positive; if heat is transferred out of the system (negative Q), then ∆U is negative.
Example 9.14 A 0.5 mol sample of an ideal gas is brought from state a back to state a along the path shown in the following P–V diagram:
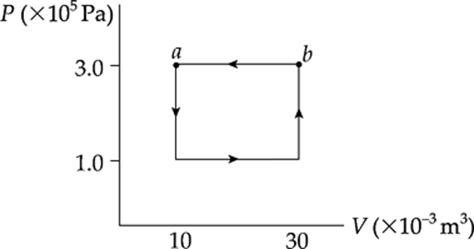
What are the values of each of the following?
(a) the change in the internal energy of the gas
(b) the work done on the gas during the process
(c) the heat added to the gas during the process
Solution. A process such as this, which begins and ends at the same state, is said to be cyclical.
(a) Because the final state is the same as the initial state, the internal energy of the system cannot have changed, so ∆U = 0.
(b) The total work involved in the process is equal to the work done from c to d plus the work done from b to a,
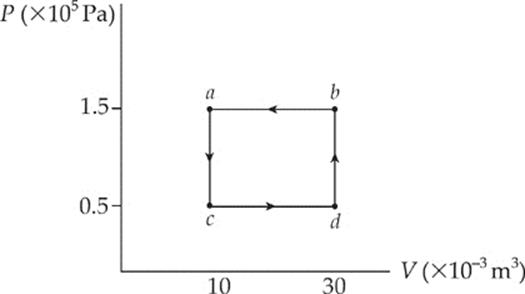
because only along these paths does the volume change. Along these portions, we find that
Wcd = –P∆Vcd = (0.5 × 105 Pa)(+20 × 10–3 m3) = –1,000 J
Wcd = –P∆Vba = (1.5 × 105 Pa)(–20 × 10–3 m3) = +3,000 J
so the total work done is W = +2,000 J. The fact that W is positive means that, overall, work was done on the gas by the surroundings. Notice that for a cyclical process, the total work done is equal to the area enclosed by the loop, with clockwise travel taken as negative and counterclockwise travel taken as positive.
(c) The First Law of Thermodynamics states that ∆U = Q + W. Since ∆U = 0, it must be true that Q = –W (which will always be the case for a cyclical process, so Q = –2,000 J.
Example 9.15 A 0.5 mol sample of an ideal gas is brought from state a to state d along an isotherm, then isobarically to state c and isochorically back to state a, as shown in the following P–V diagram:
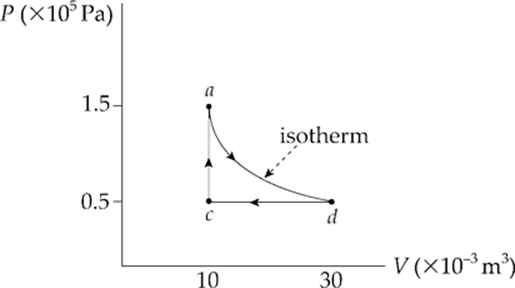
A process that takes place with no variation in temperature is said to be isothermal. Given that the work done during the isothermal part of the cycle is –1,650 J, how much heat is transferred during the isothermal process, from a to d?
Solution. Be careful that you don”t confuse isothermal with adiabatic. A process is isothermal if the temperature remains constant; a process is adiabatic if Q = 0. You might ask, How could a process be isothermal without also being adiabatic at the same time? Remember that the temperature is determined by the internal energy of the gas, which is affected by changes in Q, W, or both. Therefore, it”s possible for U to remain unchanged even if Q is not 0 (because there can be an equal but opposite W to cancel it out). In fact, this is the key to this problem. Since Tdoesn”t change from a to d, neither can the internal energy, which depends entirely on T. Because ∆Uad = 0, it must be true that Qad = –Wad. Since Wad equals –1,650 J, Qad must be +1650 J. The gas absorbs heat from the reservoir and uses all this energy to do negative work as it expands, pushing the piston upward.
THE SECOND LAW OF THERMODYNAMICS
The form of the Second Law of Thermodynamics that we”ll study for the AP Physics Exam deals with heat engines.
Converting work to heat is easy—rubbing your hands together in order to warm them up shows that work can be completely converted to heat. What we”ll look at it is the reverse process: How efficiently can heat be converted into work? A device that uses heat to produce useful work is called a heat engine. The internal-combustion engine in a car is an example. In particular, we”re only interested in engines that take their working substance (a mixture of air and fuel in this case) through a cyclic process, so that the cycle can be repeated. The basic components of any cyclic heat engine are simple: Energy in the form of heat comes into the engine from a high-temperature source, some of this energy is converted into useful work, the remainder is ejected as exhaust heat into a low-temperature sink, and the system returns to its original state to run through the cycle again.
Since we”re looking at cyclic engines only, the system returns to its original state at the end of each cycle, so ∆U must be 0. Therefore, by the First Law of Thermodynamics, Qnet = –W. That is, the net heat absorbed by the system is equal to the work performed by the system. The heat that”s absorbed from the high-temperature source is denoted QH (H for hot), and the heat that is discharged into the low-temperature reservoir is denoted QC (C for cold). Because heat coming in is positive and heat going out is negative, QH is positive and QC is negative, and the net heat absorbed is QH + QC. Instead of writing Qnet in this way, it”s customary to write it as QH − |QC|, to show explicitly that Qnet is less than QH. The thermal efficiency, e, of the heat engine is equal to the ratio of what we get out to what we have to put in; that is, e = ![]() . Since |W| = Qnet = QH− |QC|, we have
. Since |W| = Qnet = QH− |QC|, we have
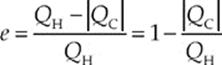
Notice that unless QC = 0, the engine”s efficiency is always less than 1. This is one of the forms of
The Second Law of Thermodynamics
For any cyclic heat engine, some exhaust heat is always produced. Because QC ≠ 0, no cyclic heat engine can operate at 100% efficiency; it”s impossible to completely convert heat into useful work.
Example 9.16 A heat engine draws 800 J of heat from its high-temperature source and discards 450 J of exhaust heat into its cold-temperature reservoir during each cycle. How much work does this engine perform per cycle, and what is its thermal efficiency?
Solution. The absolute value of the work output per cycle is equal to the difference between the heat energy drawn in and the heat energy discarded:
|W| = QH − QC = 800 J − 450 J = 350 J
The efficiency of this engine is
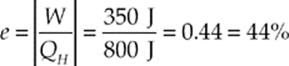
THE CARNOT CYCLE
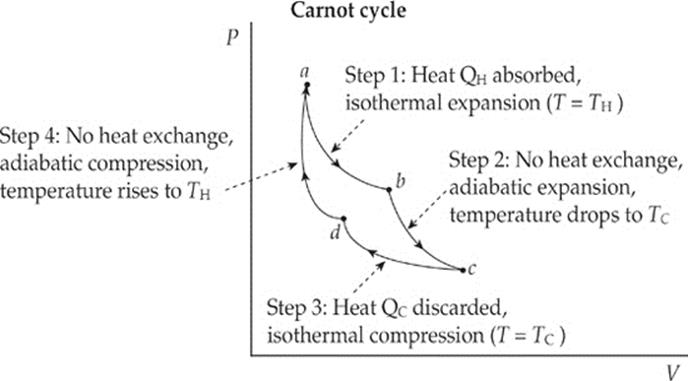
The Second Law of Thermodynamics tells us that there are no perfect heat engines. But how can we construct, in principle, the best possible heat engine, meaning one with the maximum possible efficiency (that doesn”t violate the Second Law)? Such an engine is called a Carnot engine, and the cycle through which its working substance (gas) is carried is called the Carnot cycle. It can be shown that a heat engine utilizing the Carnot cycle has the highest possible efficiency consistent with the Second Law of Thermodynamics. The cycle has four steps:
Step 1: Isothermal expansion
The system absorbs heat from the high-temperature source and expands isothermally. Because the temperature doesn”t increase, all the heat drawn from the source goes into work performed by the expansion of the gas.
Step 2: Adiabatic expansion
The system is allowed to expand without exchanging heat with its surroundings. Because the system expands (that is, does negative work), its internal energy and temperature decrease because it receives no influx of heat from the surroundings.
Step 3: Isothermal compression
Work is done on the gas by the environment and, rather than increasing its internal energy, the system discards heat to the low-temperature reservoir.
Step 4: Adiabatic compression
The system is compressed to its initial state without exchanging heat with its surroundings. Because the system is compressed, its internal energy and temperature increase, because no heat is discarded.
These four steps can be illustrated on a P–V diagram as follows:
What is the efficiency of a Carnot engine? The answer is given by the equation
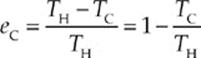
Note that the Carnot efficiency depends only on the absolute temperatures of the heat source and heat sink. The expression 1 – (TC/TH) gives the maximum theoretical efficiency of any cyclic heat engine. This cannot equal 1 unless TC = 0, that is, unless the temperature of the cold reservoir is absolute zero. But the Third Law of Thermodynamics says, in part, that absolute zero can never be reached.
Example 9.17 An inventor proposes a design for a heat engine that operates between a heat source at 500°C and a cold reservoir at 25°C with an efficiency of 2/3. What”s your reaction to the inventor”s claim?
Solution. The highest possible efficiency for any heat engine is the Carnot efficiency, and a Carnot engine operating between the temperatures TH = 500°C = 773 K and TC = 25°C = 298 has an efficiency of
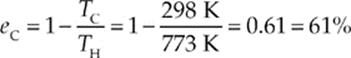
The inventor”s claim is that his engine has an efficiency of 2/3 = 67%, which is higher than eC. Your reaction should therefore be one of extreme skepticism!
CHAPTER 9 REVIEW QUESTIONS
Solutions can be found in Chapter 18.
SECTION I: MULTIPLE CHOICE
1. A container holds a mixture of two gases, CO2 and H2, in thermal equilibrium. Let KC and KH denote the average kinetic energy of a CO2 molecule and an H2 molecule, respectively. Given that a molecule of CO2 has 22 times the mass of a molecule of H2, the ratio KC/KH is equal to
(A) 1/22
(B) ![]()
(C) 1
(D) ![]()
(E) 22
2. If the temperature and volume of a sample of an ideal gas are both doubled, then the pressure
(A) decreases by a factor of 4
(B) decreases by a factor of 2
(C) increases by a factor of 2
(D) increases by a factor of 4
(E) remains unchanged
3. In three separate experiments, a gas is transformed from state Pi, Vi to state Pf, Vf along the paths (1, 2, and 3) illustrated in the figure below:
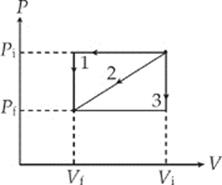
The work done on the gas is
(A) greatest for path 1
(B) least for path 2
(C) the same for paths 1 and 3
(D) greatest for path 2
(E) the same for all three paths
4. An ideal gas is compressed isothermally from 20 L to 10 L. During this process, 5 J of work is done to compress the gas. What is the change of internal energy for this gas?
(A) –10 J
(B) –5 J
(C) 0 J
(D) 5 J
(E) 10 J
5. An ideal gas is confined to a container whose volume is fixed. If the container holds n moles of gas, by what factor will the pressure increase if the absolute temperature is increased by a factor of 2?
(A) 2/(nR)
(B) 2
(C) 2nR
(D) 2/n
(E) 2/R
6. Two large glass containers of equal volume each hold 1 mole of gas. Container 1 is filled with hydrogen gas (2 g/mol), and Container 2 holds helium (4 g/mol). If the pressure of the gas in Container 1 equals the pressure of the gas in Container 2, which of the following is true?
(A) The temperature of the gas in Container 1 is lower than the temperature of the gas in Container 2.
(B) The temperature of the gas in Container 1 is greater than the temperature of the gas in Container 2.
(C) The value of R for the gas in Container 1 is ![]() the value of R for the gas in Container 2.
the value of R for the gas in Container 2.
(D) The rms speed of the gas molecules in Container 1 is lower than the rms speed of the gas molecules in Container 2.
(E) The rms speed of the gas molecules in Container 1 is greater than the rms speed of the gas molecules in Container 2.
7. Through a series of thermodynamic processes, the internal energy of a sample of confined gas is increased by 560 J. If the net amount of work done on the sample by its surroundings is 320 J, how much heat was transferred between the gas and its environment?
(A) 240 J absorbed
(B) 240 J dissipated
(C) 880 J absorbed
(D) 880 J dissipated
(E) None of the above
8. What”s the total work performed on the gas as it”s transformed from state a to state c, along the path indicated?
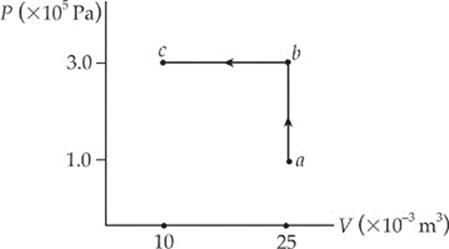
(A) 1,500 J
(B) 3,000 J
(C) 4,500 J
(D) 5,000 J
(E) 9,500 J
9. In one of the steps of the Carnot cycle, the gas undergoes an isothermal expansion. Which of the following statements is true concerning this step?
(A) No heat is exchanged between the gas and its surroundings, because the process is isothermal.
(B) The temperature decreases because the gas expands.
(C) This step violates the Second Law of Thermodynamics because all the heat absorbed is transformed into work.
(D) The internal energy of the gas remains constant.
(E) The internal energy of the gas decreases due to the expansion.
10. What”s the maximum possible efficiency for a heat engine operating between heat reservoirs whose temperatures are 800°C and 200°C?
(A) 25%
(B) 33%
(C) 50%
(D) 56%
(E) 75%
SECTION II: FREE RESPONSE
1. When a system is taken from state a to state b along the path acb shown in the figure below, 70 J of heat flows into the system, and the system does 30 J of work.
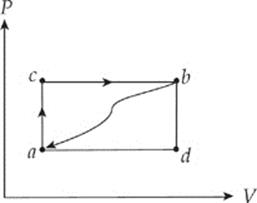
(a) When the system is returned from state b to state a along the curved path shown, 60 J of heat flows out of the system. Does the system perform work on its surroundings or do the surroundings perform work on the system? How much work is done?
(b) If the system does 10 J of work in transforming from state a to state b along path adb, does the system absorb or does it emit heat? How much heat is transferred?
(c) If Ua = 0 J and Ud = 30 J, determine the heat absorbed in the processes db and ad.
(d) For the process adbca, identify each of the following quantities as positive, negative, or zero:
![]()
2. A 0.4 mol sample of an ideal diatomic gas undergoes slow changes from state a to state b to state c and back to a along the cycle shown in the P–V diagram below:
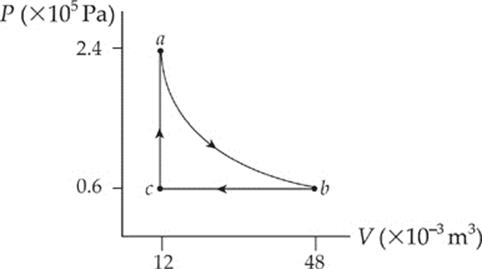
Path ab is an isotherm, and it can be shown that the work done by the gas as it changes isothermally from state a to state b is given by the equation
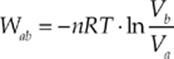
The molar heat capacities for the gas are CV = 20.8 J/mol·K and CP = 29.1 J/mol·K.
(a) What”s the temperature of
(i) state a?
(ii) state b?
(iii) state c?
(b) Determine the change in the internal energy of the gas for
(i) step ab
(ii) step bc
(iii) step ca
(c) How much work, Wab, is done by the gas during step ab?
(d) What is the total work done over cycle abca?
(e) (i) Is heat absorbed or discarded during step ab?
(ii) If so, how much?
(f) What is the maximum possible efficiency (without violating the Second Law of Thermodynamics) for a cyclical heat engine that operates between the temperatures of states a and c?
SUMMARY
· The amount of heat added to a substance and its corresponding change in temperature is related by the formula ∆Q = mc∆T. In an isolated system Qgained + Qlost = 0
· For phase changes there is no temperature change and the equation that relates the amount of heat needed to change a certain mass to its new state is given by Q = mL
· For most objects as heat is added they will expand (the notable exception is water between 0 and 4°C). For solids the equations associated with this include
∆![]() = α
= α![]() o∆T for length changes
o∆T for length changes
∆V = βV0 ∆T for volume changes
· The rate at which heat is transferred is given by H = ![]() or H =
or H = 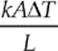 where k is the thermal conductivity (a property of the material), A is the cross-sectional area, ∆T is the temperature difference between the two sides and L is the thickness or distance between the two ends of the material.
where k is the thermal conductivity (a property of the material), A is the cross-sectional area, ∆T is the temperature difference between the two sides and L is the thickness or distance between the two ends of the material.
· For gases there are a few common equations to understand:
Pressure is defined as the fore per unit area (P = ![]() )
)
The ideal gas law is expressed as either PV = nRT or PV = NkBT
The average kinetic energy of the gas molecules is given by Kave = ![]() kbT
kbT
The average speed of a molecule of the gas is given by vrms = 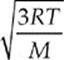 or vrms =
or vrms = 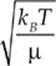
· The work done on a gas is given by W = –P∆V or can be found by the area under a pressure-vs.-volume graph.
· The First Law of Thermodynamics is ∆U = Q+W where ∆U depends only on the temperature change.
· The thermal efficiency is given by e = ![]() or e =
or e = 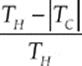 for a Carnot engine
for a Carnot engine
· W positive (or negative) means energy is being added to (or subtracted from) the system by means of work done on the system by the surroundings (or on the surroundings by the system).
· Q positive (or negative) means energy is being added to (or subtracted from) the system by means of a flow of heat from the higher temperature surroundings (or system) to the lower temperature system (or surroundings).
Note: Some textbooks define work in thermodynamics in a different way: Work is considered to be positive when work is done on the surroundings. This is consistent with the idea that the overall objective of a heat engine is to produce external (positive) work. Under this definition, the First Law must be written as U = Q – W (or U + W = Q), and W must then be interpreted differently from Q. That is, while Q is still positive when heat is being added to the system, W is now positive when work is being done by the system on the surroundings (thus decreasing the internal energy of the system).