Homework Helpers: Physics

Introduction—Necessary Skills

Trigonometry

Physics is a skill-based course. Students who begin their study of physics without the appropriate skill base must develop their skills quickly or risk struggling with the course. It is an unfortunate fact that some students fail to learn physics not because of the science, but because of the mathematics required in the course. The best way to keep the frustration level low is to keep the skill level high. In this section, I will quickly identify and review some of the skills and concepts that will help you succeed in physics. For the sake of space, this will represent a brief review, as I want to fill most of these pages with physics rather than basic math.

Like chemistry, physics is a quantitative subject, which uses numbers and units to represent physical quantities. Each number must be recorded with a unit. Otherwise its meaning can be misunderstood. For example, if you read the recorded speed of a car was 45, with no units, you could not be sure of how fast the car was traveling. You might assume that it meant 45 miles per hour, but it could just as easily have been 45 meters per second or 45 kilometers per hour. To avoid confusion, we would record a speed of 45 meters per second as 45 m/s. The sooner that you can get in the habit of recording units with every number, the better. This habit will have a positive effect on your exam scores.

We will be using the International System of Measurements (or SI), which you may be familiar with from earlier science courses. The SI limits the number of base units used in measurements to the following seven:

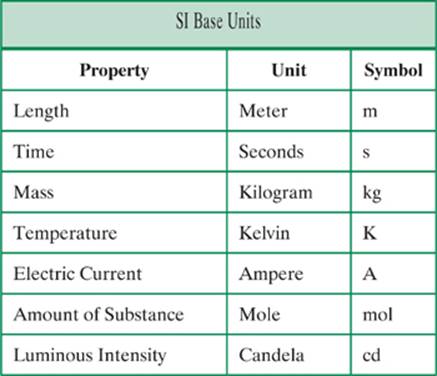
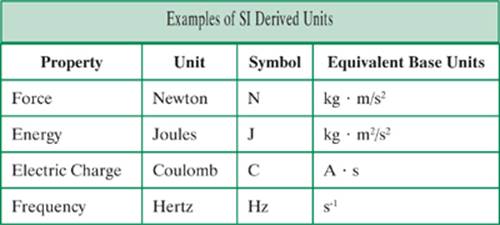
As you study physics, you will encounter the first five properties and units fairly often. When you encounter other units, such as miles or minutes, you may need to convert to SI units in order to solve a problem correctly. You will also encounter a number of derived units. Derived units are some combination of base units, which are often given a special name and symbol. For example, the newton (N) is a common derived unit for force. One newton is equivalent to 1 kg · m/s². When doing calculations with derived units, you may need to make conversions to like units. For example, it wouldn’t be appropriate to divide a value in newtons by another value in minutes. You would change the minutes to seconds before doing the calculation.

Not only should each number be recorded with units, each number should be recorded to the correct number of significant digits. You should find out, as early as possible, if your instructor will require you to round each answer to the correct number of significant digits. Students who never learn to round correctly may end up losing a point on each calculation on every quiz or exam they take each year, and all those points add up! Even if your instructor doesn’t require significant digits, most standardized exams do. It is certainly in a student’s best interest to learn to round properly as early as possible.

There are two important parts to working with significant digits. First, you need to be able to identify the number of significant digits shown in a number. Second, you need to be able to round answers correctly, based on the number of significant digits in the original problem. I will present a quick review of both of these topics now, but for a much more detailed explanation you can read Homework Helpers: Chemistry, also from Career Press.

You determine the number of significant digits shown in a number by following these rules:

1. Any nonzero digits are always considered significant.

2. Zeros that are found between two significant digits are significant.

3. Zeros that are found to the right of both a decimal and another significant digit are significant.

4. Zeros that appear solely as placeholder are not considered significant.

In addition to these rules, it is important to note that counting numbers are considered to have an infinite number of significant digits. Counting numbers are things that you actually count, rather than measure.

When dealing with a number that is written in scientific notation, you only analyze the coefficient when determining the number of significant digits present.

453 has three significant digits, because of rule one: Each digit is a nonzero digit.

3007 has four significant digits because of rules one and two: The 3 and the 7 are nonzero digits, and both zeros are found in between two other significant digits.

35.00 has four significant digits because of rules one and three. The 3 and the 5 are nonzero digits, and both zeros are found to the right of both a decimal and a significant digit.

0.0008 has one significant digit because of rules one and four: The 8 is a nonzero digit and is significant. The four zeros shown in the number are just placeholders. Remember: Rule three says that the zeros must be to the right of both a decimal place and a significant digit to be considered significant.

400 has only one significant digit because of rules one and four: The 4 is a nonzero digit, making it significant. The two zeros are not covered by rules two or three, so they are merely placeholders.

4.00 × 10³ has three significant digits because of rules one and three: The 4 is a nonzero digit and the two zeros are shown to the right of both a decimal place and a significant digit.

When you do calculations based on measurements, you must round your answer to the proper number of significant digits, based on the following rules:

1. For multiplication and division, your answer must show the same number of significant digits as the measurement in the calculation with the least number of significant digits. For example,

3.40 cm × 12.61 cm × 18.25 cm = 782.4505 cm³ before rounding.

We can’t report an answer with seven significant digits if the measurement with the least number of significant digits in our calculation, 3.40 cm, shows only three significant digits. We must round our answer to three significant digits, giving us a rounded answer of 782 cm³.

2. For addition and subtraction, your answer must show the same number of decimal places as the number in the calculation with the least number of decimal places. For example,

22.530 m/s – 8.07 m/s = 14.46 m/s.

In this example, our answer would be correct as shown. The measurement with the least number of decimal places, 8.07 m/s, is reported to the hundredths place. Our answer must also be reported to the hundredth place as 14.46 m/s.

There will be times when you see answers, in this book and others, that are written in scientific notation, and you might not be sure why. Often, answers are written in scientific notation just to express the answer in the correct number of significant digits. Look at the following example.

8.0 m × 50.0 m = 400 m²

The measurement in this calculation with the least number of significant digits, 8.0 m, shows two significant digits. Our answer only shows one significant digit. We can write this answer in scientific notation just for the purpose of showing the same value with two significant digits. Our answer would be expressed as

4.0 × 10² m².

There is another method for showing the number 400 with two significant digits. You might see it written with a line over the first zero, as in 400. The line indicates that the zero, which would not be considered significant under the rules we covered, is indeed significant.

A third method for showing additional significant digits involves using a decimal at the right of a significant digit of zero. For example, if you wanted to show the number 700 with three significant digits, you could put a decimal point to the right of the second zero, as in 700., or you could use either of the other two methods described here. For this book, we will be using decimals and/or the scientific notation method.

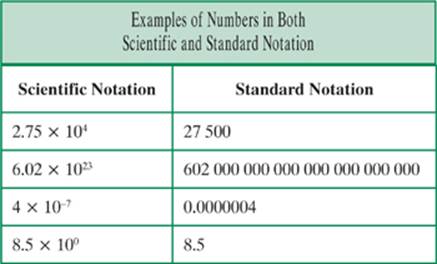
Physics is similar to chemistry, astronomy, and other sciences in that it deals with very large and very small numbers. To avoid having to write and work with long numbers, scientific notation is often employed. A number that is written in scientific notation consists of three parts: the coefficient, base, and exponent.

If the number is written properly, the coefficient will be greater than or equal to one, but less than 10. The base will be 10, and the exponent will be a number that indicates the number of places that the decimal in the coefficient needs to be moved. Examples of some numbers in scientific notation and the values they represent are shown here:

Many of the calculations that you perform in physics will represent the motion of an object in one- or two-dimensional space. Other calculations will represent a transfer of energy from one system to another. When dealing with these calculations, it is easier to keep track of the direction of a change if we assign positive and negative signs to our values. For example, we can assign a positive sign to the heat that is gained by a body of water, and a negative sign to the heat that is lost by the body of water. Or we could assign a positive sign to the velocity of a baseball as it moves upward, and a negative sign to the motion of the baseball as it moves downward.

The important thing to remember about these sign conventions is that they are arbitrary. One text may refer to acceleration in the downward direction as negative, while another refers to the same acceleration as positive. Depending on how you do your calculations, you may get the answer with the same direction, but the opposite sign. The reason for this may be as simple as you assigning a positive to a direction that the text is assigning a negative to. When working on calculations in physics, pay careful attention to signs.

When an object moves around, on, or near Earth, it pushes past air molecules. For example, when you walk down a hallway, you displace air molecules as you move forward. These air molecules offer a certain amount of resistance, but under ordinary conditions, you don’t feel it. If you have ever walked into a strong wind, you have experienced significant air resistance.

For a physics student, air resistance can be a tricky thing because it is so variable. Atmospheric conditions, such as air pressure, change from day to day and location to location. Rather than trying to take unpredictable air resistance into account when doing calculations, you will often be told to “ignore air resistance” or even to “ignore friction” in general. Some students feel that this omission makes the calculations that they are doing invalid. This is not the case. The calculations that you will learn do a good job of describing the world around you. The air resistance that you are ignoring is not always significant, and most of the motion that takes place in our universe takes place in areas of space where there would be no significant air resistance. More importantly, the air resistance on Earth is so variable that it is not possible to take it into account in every situation.

For your part, you should assume that the calculations that you see performed in class, and in this book, don’t take air resistance into account unless otherwise noted. Don’t let this make you feel that the problems that you carry out in class are “fake” or inaccurate. As you will learn from your lab experiences, these calculations will allow you to predict the motion of real objects to a great degree of accuracy.

Mathematics is the language of physics, and you can’t study physics without encountering numerous symbols and formulas. Some symbols are used universally, and will likely appear the same in all texts. For example, acceleration always seems to be represented by a lowercase a. What may confuse you in the beginning is that not all quantities will be represented by the same symbol in every text or every class. Different teachers and different texts will often use different symbols to represent the same quantity. For example, some texts will use the symbol d to represent displacement, while others will use Δx or Δp or Δs to represent the same quantity. As a result of the use of different symbols to represent the same quantities, formulas using these symbols may appear quite different, even if they mean the same thing! For example, the following set of formulas show the same relationships, yet they appear quite different to a novice physics student.

If all of these formulas look so different, is there one that is the “correct” formula? That’s like asking which of several sketches of a person is the “correct” sketch. All of the formulas shown actually represent the same thing, and an experienced physics or math student will probably see that right away. Yet beginning physics students usually only become familiar with the “look” of the formulas and symbols that they see in class or in their particular text. A problem might arise when they pick up a different book, or if they take a standardized test and are given a formula sheet with formulas that they fail to recognize.

Examples of Formulas That Look Different, Yet Represent the Same Calculation

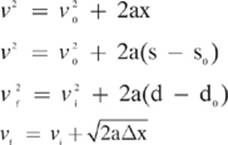
The solution to the problem is quite simple. Don’t grow too attached to a particular symbol or formula. Think of the letters or symbols that are used to represent physical quantities as arbitrary. Instead of trying to memorize how a particular formula looks, try to understand and recall the relationships between the physical quantities involved. For example, if you remember the relationship between speed, distance, and time,

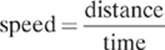
it won’t matter to you if distance is represented by d or x or Δp, because you can still recognize or derive a proper formula.

There is probably no more significant barrier to learning introductory physics than a weakness in algebra. Students who are unable to isolate each of the possible unknown quantities in the many formulas they encounter in physics tend to run into trouble in the first couple weeks of class. If your study of physics uncovers a weakness in algebra, it is best to take care of that problem first, so that you don’t develop a negative attitude toward the science. Fortunately, the algebraic skills necessary for the study of basic physics are relatively simple, and a brief review may be all that you need.

Let’s look at an example of a physics formula, and go through the isolation of each of the possible unknown quantities. If you want to test yourself, write the following equation on a piece of paper and try to isolate each of the variables, one at a time. Then check back here to compare your answer to the work shown following the equation.

The formula is already shown with d isolated. Let’s go over methods for isolating g and Δt.

Now, we will go back to the original formula and solve for Δt.

Of course, you don’t have to follow the steps shown here in this exact order. The important thing is that the final equations look the same. If you were able to successfully isolate the unknown quantities in the preceding formula, then you probably possess the algebraic skills required to succeed in physics. If, however, you need more help, I would recommend that you purchase Homework Helpers: Algebra, also from Career Press.

Trigonometry is the branch of mathematics concerned with studying the properties of right triangles. At first, it might not be clear to you how this may pertain to the study of physics, so I will give you an example. Suppose a person was pushing on the handle of a shopping cart, exerting a force of 20.0 newtons (N) at an angle of 30.0° below the horizontal, represented by the black arrow in Figure 0.1. In order to calculate the acceleration of the shopping cart, you want to know how much of the applied force (F), or push, is being exerted “downwards” and how much of the force is being exerted “forwards.”

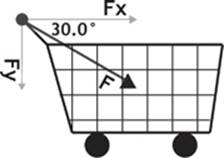
Figure 0.1

Notice that the downward component of the force (F_y) is perpendicular to the forward, or horizontal, component of the force (F_x). This means that the components are at a right angle to each other. We can sketch the problem that we are trying to solve as a right triangle, using the original force of 20.0 N as the hypotenuse, and the horizontal and vertical components as the other sides. Furthermore, we can add the angles that we know. Because all of the angles in a triangle must add up to 180°, we can determine the third angle as well, but I will leave it out of Figure 0.2 to avoid confusion.

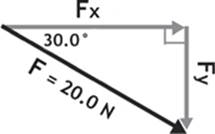
Figure 0.2

We can solve for the missing sides of our triangle using some of the following trigonometry functions.

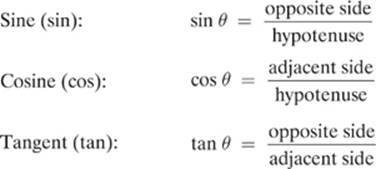
The hypotenuse of our triangle is the original force of 20.0 N. Working with our original 30.0° angle, we can see that the vertical component of the force (F_y) represents the opposite side. Knowing this angle and the hypotenuse, we can solve for the horizontal component (opposite side), as shown here:

Isolating the opposite side:

We get:

opposite side = hypotenuse × sin θ = (20.0N)(sin 30.0°) = 10.0 N

So, the vertical component of the original force is 10.0 N.

We can also find the horizontal component of the original force, keeping in mind that it represents the adjacent side to our original angle of 30.0°.

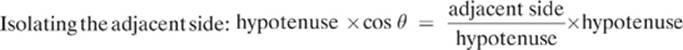
We get:

So, the horizontal component of the original force is 17.3 N.

Alternatively, we could have found the last missing side using the Pythagorean theorem:

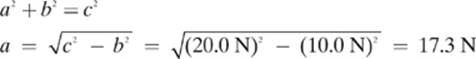
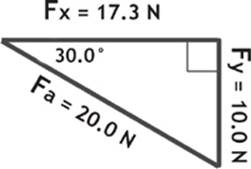
Figure 0.3

At other times, you will want to use trigonometry functions for finding the missing angle in a triangle. Let’s suppose there is a river where the water flows with a velocity of 8.00 m/s (meters per second) east. A man crosses the river in a boat with a velocity of 20.0 m/s north, relative to the water. The water pushes the boat east during the crossing, so that to an observer on the shore, the boat seems to head northeast as it crosses. How would we find both the magnitude and direction of the resultant velocity?

The velocity of the boat (V_b) and the water (V_w) are perpendicular to each other, so finding the magnitude of the resultant velocity isn’t hard. We can turn the sketch into a right triangle and use the Pythagorean theorem again.

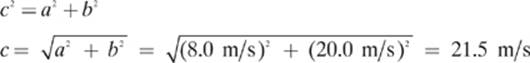
To find the angle between the intended path and the actual path of the boat, we make use of one of the following trigonometry functions.

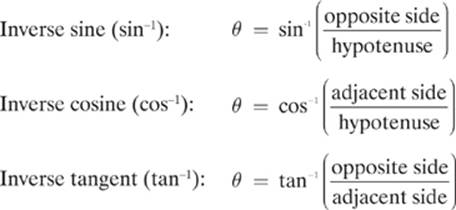
It makes sense to use the inverse tangent for this problem, so that we can make use of the numbers that came with the actual problem. Personally, I would avoid using a function involving the hypotenuse in this particular case, because if we made an error finding that value, the error would carry over to our answer for the angle. Solving for the angle we find:

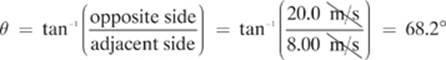
So, the resultant velocity (V_r) of the boat crossing the river is 21.5 m/s at an angle of 68.2° north of east.

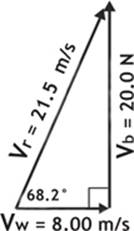
Figure 0.4