Homework Helpers: Physics

2 Forces and the Laws of Motion

In this chapter we will begin to study forces and the effects that forces have on objects. A force is simply a push or a pull. You exert a force on a door when you push it open or pull it closed. Earth exerts a force on the moon, allowing it to stay in orbit. Sometimes your sweater might exert a force on a sock after you take them out of the dryer, resulting in what is called “static cling.” Forces exert an influence on objects, sometimes causing them to move and sometimes causing them to stop. Let”s explore these forces and motion in more detail.

We spend our whole lives living under the influence of various forces. The force of gravity exerted by Earth keeps us on the ground. The electrostatic force of repulsion between our electrons and the floor”s electrons keeps us from falling through it. The force of friction between our shoes and the floor allows us to move forward. A strong nuclear force keeps the subatomic particles in the nuclei of our atoms from flying apart. You exert a force on a fork to move it toward your mouth, so your teeth can exert forces on some food. Get the idea?

Despite being surrounded by forces, many people have a hard time defining or describing forces. In simplest terms, we describe a force as a push or a pull. Alternatively, we can think of a force as something that is capable of changing the velocity of an object. Remember: The velocity of an object includes both speed and direction, so a force can change either one or the other, or both.

Force
A push or a pull. Something that is capable of changing an object”s velocity.

Some forces are called contact forces. Contact forces require contact between two objects. We need to touch a door to push it open, so that is an example of a contact force. Other forces, called field forces, don”t require physical contact to work. Field forces, which include gravity and magnetism, act over distances. The sun is so far away from Earth that it takes light, which can travel at 3.00 × 10⁸ m/s, about 8 minutes to get here from there. However, even across that incredible distance, some 1.5 × 10⁸ km (or 9.3 × 10⁷ miles), the force of gravity between the sun and Earth keeps our planet in orbit! And yet, physicists consider gravity a relatively weak force!

Figure 2.1

Forces are vector quantities, which means that a direction is required to describe them completely. At any given moment, an object can have several forces exerted on it. Imagine, for example, a student is pushing on a desk (exerting a force on it), causing it to slide (change its velocity) across the floor.

There are a number of forces acting on the desk. Because each force is a vector, all of the forces can be added together, using the techniques described in Chapter 1, to find the resultant vector. This resultant force vector is sometimes referred to as the net force (F_net) acting on the object.

Net Force (F_net)—The vector sum of all of the forces acting on an object.

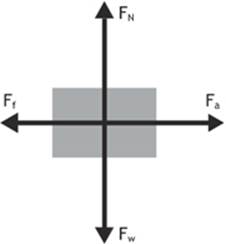
Figure 2.2

When you want to determine the net force acting on an object, it is often useful to draw a free-body diagram. A free-body diagram is a simple sketch that highlights the forces acting on an object. The object can be represented with a simple geometric shape, such as a square or circle. The forces acting on the object are represented by arrows. Each arrow points in the direction of the force it represents, and the length of the arrow can give an indication of the relative magnitude of the force. However, it is not always practical to draw the vectors to scale, as some forces involved may be much larger than others. Examine the free-body diagram of the desk with the student pushing on it.

Do you recognize what each of the arrows shown in Figure 2.2 represent? The applied force (F_a) is the force being exerted by the student on the desk. The weight (F_w) is the force exerted by Earth on the desk. The normal force (F_N) is the force being exerted by the floor on the desk perpendicular to the surface of the floor, and, as you can surmise from the length of the respective arrows, it is equal to the magnitude of but opposite in direction to the force of weight. The friction (f_f) is the force exerted on the desk by the floor in the direction opposite to its motion, and, judging by the length of the respective arrows, it is less than the applied force and in the opposite direction.

Notice that the free-body diagram only shows the forces acting on the desk, because that is the object that we are interested in. We don”t include the forces the desk is exerting on the student or the floor, because that is not what we want to focus on.

Let”s try a problem where we are asked to draw a free-body diagram and solve for the net force being exerted on a desk.

Example 1

A student applies a force of 80.0 N to a desk with a weight of 700.0 N in a direction that is horizontal to the surface of the floor. The force of friction between the desk and the floor is 60.0 N. Draw a free-body diagram and find the net force acting on the desk.

We can sketch the desk as a simple rectangle and represent each of the forces with an arrow. If we wanted to draw the forces to scale, we could make up a scale. For example, we could say 20.0 N = 1.00 cm, and draw the vectors to scale. However, we will be adding the vectors algebraically, so I won”t be drawing my diagram to scale.

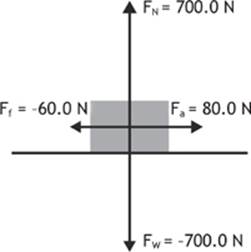
Figure 2.3

As far as the forces go, the problem only mentioned three. There is no mention of the normal force exerted upwards by the floor on the desk. Problems often fail to mention that force because they expect students to realize that the force is there, and that, in situations like the one described here, it is always equal to the weight in magnitude. The reason for this will be explained in Lesson 2–4. If the normal force wasn”t there, or if it was less than the weight of the desk, the desk would fall through the floor! Always be sure to add the normal force to this type of problem.

Now let”s calculate the net force acting on the desk. Let”s designate upward as positive and downward as negative. Let”s also make the direction of the applied force positive and the direction of the force of friction negative.

Given: F_a = 80.0 N F_f = –60.0 N F_w = 700.0 N F_N = –700.0 N

Find: F_net

We need to analyze the horizontal and vertical forces independently.

Solution: F_nety = F_w + F_N = 700.0 N + (–700.0 N) = 0 N

F_netx = F_a + F_f = 80.0 N + (–60.0 N) = 20.0 N

We have a net force of 20.0 N horizontal to the surface of the floor.

Of course, force vectors can be added together even if they don”t lie along the same axis, using the methods we showed for velocity vectors in Lesson 1–1. Try the following example on your own, and then check my answer.

Example 2

Two students attempt to push a box by exerting forces of 28.0 N to the east and 35.8 N to the north respectively, at right angles to each other, as shown in the free-body diagram in Figure 2.4. Find the resultant force applied by the two students.

Given: F₁ = 28.0 N F₂ = 35.8 N

Find: Resultant force (F_r)

Let”s take our two component forces and make a triangle with them and the resultant force.

Solution: We can find the magnitude of the resultant force using the Pythagorean theorem.

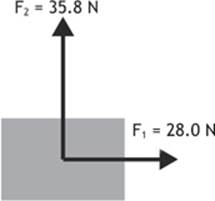
Figure 2.4

We find the direction of the force using tan^–1:

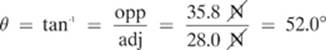
Our resultant force is 45.4 N at 52.0° north of east.

So, now you should understand what a force is. In the next few lessons you will be learning more specifically what a does.

Try the following review questions before moving on to the next lesson.

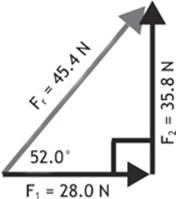
Figure 2.5

Lesson 2–1 Review

1. _______________ is the vector sum of all of the forces acting on an object.

2. If a boy applies a horizontal force of 12.0 N to push a book across a table, where the force of friction between the book and table is 6.5 N, what will be the net force on the book?

3. If a force of 5.00 N acts concurrently (at the same time) with a 8.00 N force on the same object, at right angles to each other, what will be the magnitude of the resultant force?