Homework Helpers: Physics

2 Forces and the Laws of Motion

You have probably heard and may have even used the expression “for every action, there is an equal and opposite reaction.” This expression is actually a rephrasing of Newton”s third law of motion, the law of action-reaction. There is something that bothers me about this expression, because I believe it leads to a certain amount of confusion on the part of students. When a baseball bat hits a baseball, the bat and the ball don”t seem to react the same way. Better yet, when a car hits a deer in the road, the car doesn”t seem to react in the same way as the deer. The car may get damaged and slow down a small amount, but the deer probably gets killed, and may even be thrown some number of feet. How are these “equal and opposite” reactions? Does Newton”s third law not apply in this case?

Newton”s third law actually states that if an object exerts a force on a second object, the second object exerts an equal and opposite force on the first object. It is actually the forces exerted between two objects that are equal and opposite, not what we might think of as the “reactions” of the objects.

Newton”s Third Law
The Law of Action-Reaction

When an object exerts a force on a second object, the second object exerts an equal and opposite force on the first object.

Newton”s third law can be seen in countless real-life situations. For example, if you punch your brother in the face (and I am certainly not recommending it), in addition to getting grounded by your parents, you will probably end up with a hurt fist. Why does it hurt your hand when you punch something or someone? Newton”s third law. You can”t touch without being touched. If your fist exerts a force on his face, his face will exert an equal and opposite force on your fist. This is an example of what we will refer to an action-reaction pair of forces.

In our example with a baseball and a bat, the bat exerts a force on the ball and the ball exerts an equal and opposite force on the bat. For example, if the bat exerts a 20.0 N force due east on the ball, the ball exerts a 20.0 N force due west on the bat. The two objects don”t “react” to these respective equal forces in the same way, because each object has its own mass. The mass of the bat is much greater, so it doesn”t experience as great an acceleration as the ball, as explained by Newton”s second law, F = m a. Let”s look at this example more closely.

Example 1

A baseball bat with a mass of 5.00 kg exerts a force of 20.0 N on a 0.250 kg baseball. Find the resultant acceleration of each object.

This question requires we use both Newton”s second and third laws to solve it. The third law tells us that if the bat exerts a 20.0 N force on the ball, the ball exerts a 20.0 N force on the bat. To show that the forces are in opposite directions, we will call one positive and one negative. It is arbitrary which force we call negative, but I will choose to call the “reaction” force—that is, the force exerted by the ball on the bat—negative.

As you can see, both objects experience equal and opposite forces, but they react to these forces in very different ways. The ball experiences a much greater acceleration because it has much less mass. The bat is more massive, so a smaller acceleration results. The fact that the accelerations are in different directions makes sense, because each object will experience an acceleration in the direction of the net force on it. The ball will actually change directions and head in the direction of the force applied by the bat, while the bat only slows down in the direction of the force applied on the bat.

When a book is placed on a table, it will exert a downward force on the table that is equal to its own weight. The table must exert an equal and opposite force on the book, according to Newton”s third law. If the table exerted a reactionary force that was less than the weight of the book, the book would break the table and fall toward the ground. If the table exerted a reactionary force that was greater than the weight of the book, the book would actually be pushed upwards, off of the table.

Example 2

A book with a mass of 1.50 kg rests on a table. Find the weight of the book (F_w) and the force being exerted by the table on the book (F_N).

Given: m = 1.50 kg g = –9.81 m/s²

Find: F_w and F_N

Solution: The weight of the book:

F_w = mg = (1.50 kg)(– 9.81 m/s²) = –14.7 N

The negative sign in the answer simply indicates that the force is directed downward. This force of weight is equal to the force that the book will exert on the table. The table must be exerting an equal and opposite force, so F_N = –F_w = 14.7 N.

where the positive value indicating that the force is directed upward.

It is important to point out that, though the force exerted by the table on the book in Example 2 was equal and opposite to the book”s weight, these forces do not represent action-reaction force pairs. The force pairs are the force exerted by the book on the table and the force exerted by the table on the book. What is the force that is the equal and opposite force to the force of weight?

One of the most profound aspects of Newton”s third law comes from the understanding that this law holds true for all types of forces, including forces at a distance. This means that when Earth exerts a force on you, due to gravity, you exert an equal and opposite force on Earth! If you were to jump off your bed, you would fall to the floor because Earth is pulling you down with a force equal to your weight in newtons. What you might not realize is that you are also pulling the Earth up with an equal and opposite force! Newton”s laws tell us that you have the power to move planets!

“Impossible!” you say? Suppose I tell you that the mass of a boy is 60.0 kg. You can use this information and the acceleration due to gravity (–9.81 m/s²) to find the boy”s weight, as described in our last lesson. This weight is the force exerted on the boy by Earth, due to gravity.

The boy”s weight: F_w = m_bg = (60.0 kg)(– 9.81 m/s²) = –589 N

The negative sign in this case simply tells us that the force is being directed downward, or toward the center of Earth. Newton”s third law tells us that if Earth is exerting a force on the boy, the boy must be exerting an equal and opposite force on Earth. So, the boy is also exerting a 589 Nforce on Earth. For the sake of simplicity, let”s pretend that this represents an unbalanced, or net, force. Now, if I tell you that the mass of Earth (m_e) is 5.98 × 10²⁴ kg, can you determine the acceleration of Earth as a result of the reaction force to the boy”s weight? Let”s try the following calculation together.

Example 3

A 589 N boy jumps off his bed. As he falls to the floor, he accelerates downward at a rate of –9.81 m/s² due to gravity. Earth has a mass (m_e) of approximately 5.98 × 10²⁴ kg. Use this information to find the rate of the acceleration of Earth upward toward the boy (a_e).

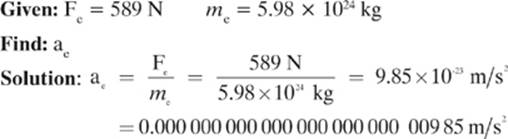
Do you see how insignificant the acceleration of Earth would be in this is situation? Combine that with the fact that the boy is in the air for a fraction of a second, and you can see why the boy”s effect on the planet Earth is not noticeable. The force really is there, but a Ping-Pong ball has a better chance of knocking down a house than the boy does of causing problems for Earth.

Let”s try some practice questions before moving on to the next lesson.

Lesson 2–4 Review

1. If a rock with a mass of 2.45 kg rests on a horizontal driveway, what is the magnitude of the force that the driveway is exerting on the rock?

2. According to Newton”s third law, if a car hits a garbage can, will they both experience the same acceleration?

3. Use Newton”s third law to explain what happens when someone breaks through a thin layer of ice on a pond.