Homework Helpers: Physics
2 Forces and the Laws of Motion
Lesson 2–6: Motion on an Inclined Surface
In this lesson we study motion on an “inclined plane,” which is a fancy term for a ramp. There are many real-life applications for this type of problem. Movers will sometimes use a ramp to avoid having to lift a heavy object straight up. Motion on an inclined surface can be seen at the park, where children slide down slides. Driving a car up a hill represents motion on an incline. Skiing and sleigh riding often take place on an incline as well.
Here”s a little experiment that you can try right now. Find a board or some other sturdy object that can serve as a ramp. Place a book or some other object on the board when it is lying flat.
Slowly lift one end of the board and see how steep you need to make the incline before the book starts to slide slowly down it. Now, ask yourself the important question: What makes the book slide down the ramp? The book was at rest, and then it started to move.
Newton”s second law tells us that an unbalanced force is required to set the book in motion. Where did the force come from? If you said “gravity,” you are correct. But the force of gravity was always there, even when the board was lying horizontally. The force of gravity between Earth and the book didn”t change as you changed the angle of incline of the board. So, what did change?
It will help to draw a free-body diagram for the book when it was lying on a horizontal surface, and another for when it was lying on an inclined surface. (See figures 2.9 and 2.10.)
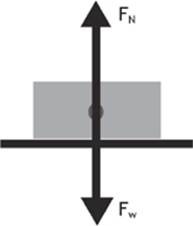
Figure 2.9
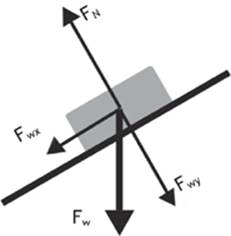
Figure 2.10
What you see is that when the book was on a horizontal surface, the normal force exerted by the board on the book was equal to the weight of the book and in the opposite direction. As you lifted one end of the board, the weight of the book is still directed straight down, but the normal force is still perpendicular to the surface of the board. If you break the force of weight of the book into two components, the normal force is still equal and opposite to the component that is perpendicular to the surface, but another component of the weight is shown parallel to the surface of the incline. Even when the book was on a slight incline, it probably didn”t move, because the parallel component of the weight is balanced by the force of static friction up to a point. When the incline gets so great that the parallel component of the book”s weight is greater than the maximum value for the force of static friction, the book begins to slide down the incline.
You can also use this set-up to test the fact that the value for kinetic friction is less than the value for static friction. Lay the board flat again, put the book on it, and then raise it to an angle that is just less than the angle that caused it to slide last time. Tap the book, and it should slide down the board, accelerating along the way. The fact that it didn”t slide before you tapped it shows that the force of static friction was not overcome until you tapped it. Once in motion, it accelerated because the parallel component of the weight was greater than the value of kinetic friction.
As you can imagine, the materials in contact will influence the angle that the board must reach before the object begins to slide. A different object, such as a glass, might have started to slide when the board was at a lesser angle. This is because there is less friction between some items. The coefficient of friction must be taken into account when dealing with most of these problems.
One way to approach inclined plane problems is to realign our x and y coordinate system so that the x-axis lines up parallel to the incline and the y-axis is perpendicular to the incline.
Let us ignore friction for a moment and begin with the most basic of inclined plane problems. For this problem, I am going to ask you to ignore the friction between the inclined plane and the object we place on it. Imagine how slippery a steep hill covered by a sheet of ice can be, and then take it further.
Example 1
A block with a mass of 5.00 kg is placed on a frictionless inclined plane at an angle of 48.0° above the horizontal. Draw a diagram for the problem and find the acceleration of the block.
Given: m = 5.00 kg θ = 48.0° g = 9.81 m/s2
Find: a
Solution:
Study Figure 2.11. It is likely that you will need to produce similar diagrams, and it is important that you understand how they are constructed.
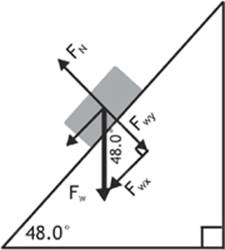
Figure 2.11
In our diagram the larger triangle represents the ramp, or inclined plane. The smaller triangle is formed from the vectors representing the force of weight of the block, and the component vectors of the weight. The weight of the block (Fw) is directed straight down toward the center of Earth, ignoring the angle of the incline. We then find the components of the weight that we are interested in. The y component (Fwy) is the component of the weight that is perpendicular to the surface of the incline, and the x component (Fwx) is the weight that is parallel to the surface of the incline. The larger and smaller triangles are similar triangles, meaning they have the same angles. Therefore, the angle between the vector representing the weight and the vector representing the perpendicular component of the weight is also 48.0°.
The y component of the weight (Fwy) will not cause the block to slide down the ramp, as it is equal and opposite to the force that the ramp exerts on the block. Therefore, the net force perpendicular to the surface of the ramp is zero. The x component of the weight (Fwx), on the other hand, will cause the block to slide down the ramp, provided it is greater than the force of friction. Let”s calculate the weight of the block using Newton”s second law, and the component of the weight that is parallel to the ramp.
Weight = Fw = mg = (5.00 kg)(9.81 m/s2) = 49.1 N
Parallel Force = Fwx = Fw sin θ = (49.1 N)(sin 48.0°) = 36.5 N
Can you see why we multiplied the weight by the sine 48.0°? The weight forms the hypotenuse of our inner triangle, and the parallel component of the weight appears as the opposite side to the 48.0°. So, we use the relationship between the hypotenuse and the opposite side, given by
![]()
Of course, we could have done the calculation in one step, and many students prefer to remember the formula for the x component of the weight as Fwx = mg sin θ.
Now we have everything we need to find the acceleration of the block down the incline. Because there is no friction, the only unbalanced force acting on the block is the parallel component of its weight. Therefore, the net force is the same as the parallel component of the weight. We can use Newton”s second law to find the acceleration.
![]()
You may have noticed that we multiplied g by the mass of the block in our first calculation, and then we divided the Fp by the mass in our last calculation. These steps actually cancel each other out! I went through each of these steps to explain to you logically what we are doing, but now I will show you the easier way to do this calculation.
![]()
Using this simplified formula to solve Example 1 we would get:
acceleration (a) = g sin θ = (9.81 m/s2)(sin 48.0°) = 7.29 m/s2.
So, we can get the same answer (with a slight difference due to rounding) with far less work! Furthermore, we don”t need to know the mass of the object to do the calculation. The key to remember is that the acceleration of an object sliding down a frictionless ramp is simply g sin θ.
Example 2
A crate slides down a frictionless ramp with an angle of 33.5° above the horizontal. Find the acceleration of the crate.
Given: g = 9.81 m/s2 θ = 33.5°
Find: a
Solution: a = g sin θ = (9.81 m/s2)(sin 33.5°) = 5.41 m/s2
Perhaps you are thinking, How often am I going to encounter a ramp with a frictionless surface in real life? Your point is well taken! Let”s try another example where we have a coefficient of friction between the block and the surface of the ramp.
Example 3
A crate with a mass of 35.0 kg is sliding down an inclined plane with an angle of 43.0° above the horizontal. If the crate is accelerating at a rate of 3.45 m/s2, find the coefficient of kinetic friction between the ramp and crate.
Given: m = 35.0 kg g = 9.81 m/s2 a = 3.45 m/s2 θ = 43.0°
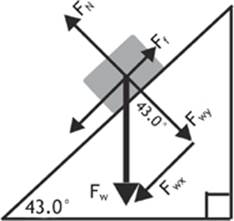
Figure 2.12
Find: μk
As a beginner, it is hard to know where to start these problems. You consider the information that you have been given and the formulas that you know, and you may not be sure how to get to what you want to find. There are actually several different ways to proceed, but I will show you how to work backwards from what you need to what you have. I will then show you how to put all of the formulas together to solve the problem in one step.
Our unknown is the coefficient of kinetic friction. From Lesson 2–5, we have the formula for determining the coefficient of kinetic friction:
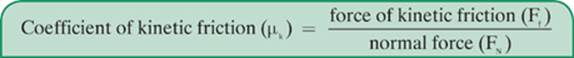
or
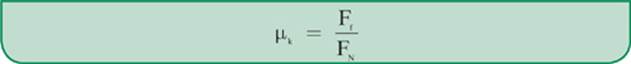
We can see from Figure 2.12 that the y component of the weight (Fwy) represents the adjacent side of our inner triangle, and this will be equal to the normal force (FN). The hypotenuse of our inner triangle is the weight (Fw) of the crate, which we find with Newton”s second law, Fw = mg. We can use the relationship between the adjacent side (Fwy) and hypotenuse (Fw) of our inner triangle, shown by
![]()
That means that the normal force is equal to
FN = – Fwy = –FW cos θ = –mg cos θ
= –(35.0 kg)(–9.81 m/s2)(cos 43.0°) = 251 N
That takes care of the denominator in our working formula.
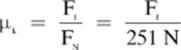
Now, all we need to do is figure out the force of kinetic friction between the crate and the ramp. From our diagram (Figure 2.12), we can see that there are two forces acting on the crate that are parallel to the surface of the ramp. The parallel component of the force of weight (Fwx) is causing the crate to slide down the ramp, while the force of kinetic friction (Ff) is working against this force.
As we learned earlier in this lesson, the parallel component (Fwx) of the weight of an object on an inclined plane can be found with the formula;
Fwx = mg sin θ. We have everything we need to find the Fwx:
Fwx = mg sin θ = (35.0 kg)(9.81 m/s2)(sin 43.0°) = 234 N.
We can use Newton”s second law, the acceleration of the crate, and the mass of the crate to find the net force (Fnet) acting on it.
Fnet = ma = (35.0 kg)(3.45 m/s2) = 121 N
The net force (Fnet) acting on this crate is going to be the sum of the two forces, Fnet = Fwx + Ff. If we isolate the force of friction in this equation, we get Ff = Fnet – Fwx. Solving for the force of friction, we find:
Ff = Fnet – Fwx= 121 N – 234 N = -113 N.
This gives us the numerator for our formula for the coefficient of kinetic friction, so we can get our final answer. We will use only the magnitude of the force of friction:
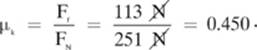
That was a lot of work, but I hope I didn”t lose you. With some practice, you should come to enjoy the puzzle-solving aspect of these problems. If you prefer to come up with one “master formula” for the problem and solve it in one calculation, it might look like the following:
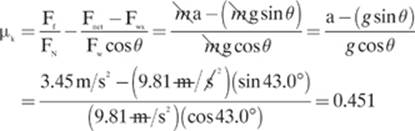
Please note that the slight difference in the two answers is due to rounding, and is not significant.