Homework Helpers: Physics
3 Work, Energy, Power, and Momentum
Like any other science, physics has its own specific language. Unlike the majority of the terms that you encounter in other sciences, many of the terms that you will encounter in physics are variations of words that you use in everyday life. The advantage to this is that you won”t need to learn the spellings of new terms, like, say, echinoderm. The disadvantage is that you might have to “unlearn,” or at least stop using some previous definitions that you know for terms such as work, power, and momentum. All in all, this should be far less painful than learning to spellendoplasmic reticulum.
Lesson 3–1: Work
At some point in your years of studying science, you probably memorized a definition for energy that went something like “Energy is the ability to do work.” Unfortunately, as is too often the case in science classes, you may have memorized the definition and never really understood what was meant by “work.” You may have assumed that your teacher was using the term work in the same way that it is used in everyday life, but that is not entirely correct. In physics, the term work has a very specific meaning. Work is defined as the product of the displacement and the component of the force in the direction of the displacement.
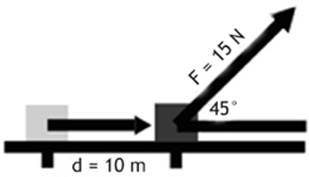
W = Fd cos θ = (15 N)(10 m)(cos 45°) = 106 N · m
Figure 3.1
Work = force applied in the
direction of motion × displacement
W = Fd cos θ
Work is measured in joules (J)
1 joule = N × m = kg × m2/s2
It is important to remember that without a displacement, the work done is equal to zero. Holding stationary objects does not count as work. The part of the work equation that shows cos θ also leads to some interesting, yet tricky, questions. The cosine of a 0° angle is equal to 1, so when the displacement and force lie along the same angle, the formula can be simplified to read W = Fd. The cosine of 90° is equal to 0, so when the applied force and the displacement are at right angles to each other, no work is done by the force. It is also important to note that although work is a scalar quantity, it can have positive or negative values. Work can be done on something, or work can be done by something.
To get a better understanding of this definition, let”s consider some examples.
Example 1
How much work is done by a weight lifter as he holds a 100.0 N barbell stationary, above his head?
The weight lifter is not displacing the weight during this time, so he is doing no work. He did work getting the barbell into its current position, but as he holds it stationary, no work is being done, as shown in the following calculation.
Given: F = 100.0 N d = 0 m θ = 0°
Find: W
Solution: W = Fd cos θ = (100.0 N)(0 m)(cos 90°) = 0 J
Example 2
A lumberjack carries a 50.0 N log on his shoulder as he walks at a constant rate for a distance of 30.0 m across a level surface. How much work does he do on the log during this period of time?
Remember: The lumberjack is walking at a constant rate across a level surface. The log is not accelerating, so there is no net force being exerted on the log along the horizontal axis. The lumberjack is exerting a constant force of 50.0 N on the log with his shoulder, but the direction is upward, at a right angle to its motion.
Given: F = 50.0 N d = 30.0 m θ = 90.0°
Find: W
Solution: W = Fd cosθ = (50.0 N)(30.0 m)(cos 90.0°) = 0 J
It is starting to seem as though nobody is doing any work. Let”s see some more examples.
Example 3
A girl exerts a force of 35.0 N at an angle of 35.0° above the horizontal along the handle of her wagon as she pulls it 25.0 m across a level sidewalk. How much work does she do on her wagon?
Given: F = 35.0 N d = 25.0 m θ = 35.0°
Find: W
Solution: W = Fd cos θ = (35.0 N)(25.0 m)(cos 35.0°) = 717 J
Example 4
Attempting to stop a runaway school bus, a superhero exerts a force of 200.0 N against the motion of the bus, slowing it to a stop over a distance of 12.0 m. How much work does the hero do on the bus?
Given: F = 200.0 N d = 12.0 m θ = 180°
Find: W
Solution: W = Fd cos θ = (200.0 N)(12.0 m)(cos 180°) = – 2.40 × 103 J
Note the fact that the work done on the bus is negative. This is because the cosine of an 180° angle is equal to –1. The net effect of this work being done on the bus will be to cause a negative acceleration on it. If you are wondering why the answer is in scientific notation, it is because our answer came out to 2,400 J, but I wanted to show three significant digits.
Do you know how much work the bus did on the superhero in Example 4? Newton”s third law tells us that if the superhero exerted a 200.0 N force on the bus, then the bus exerted a 200.0 N force on the superhero. The superhero was displaced in the same direction as the force applied on him by the bus, so the angle is 0°. The work done by the bus on the superhero would be:
W = Fd cos θ = (200.0 N)(12.0 m)(cos 0°) = 2.40 × 103 J
Sometimes you will get a tricky problem involving gravity. Consider the following example.
Example 5
A warehouse worker pushes an 80.0 kg crate a distance of 3.0 m up 22.0° incline. How much work is done against gravity?
Be careful with this one. If this question had asked for the total amount of work that the worker did, it would have be equal to
W = Fd cos θ = mg cos θ = (80.0 kg)(9.81 m/s2)(3.0 m)(cos 0°)
= 2,400 J
However, the question only asks for how much of the work that the worker does is done “against gravity.” In other words, we need to find the y component of the work. You might be tempted to just change your calculation to include the 22.0° angle, but you need to remember that the angle that we are interested in is always the angle between the displacement and the applied force, and that the question specifically asks for the “work done against gravity.” So, the angle that we are interested is actually (90° – 22.0° = 68.0°) 68.0°.
Given: m = 80.0 kg g = 9.81 m/s2 d = 3.0 m θ = 68.0°
Find: W
Solution: W = Fd cos θ = mgd cos θ
= (80.0 kg)(9.81 m/s2)(3.0 m)(cos 68.0°) = 880 J
Alternatively, we could have used sin 22.0° in place of cos 68.0° and still found the same answer, but I didn”t want to confuse anyone by changing the work formula at this point.
Finally, let”s do one last example where work isn”t the unknown. Just so we practice isolating a different variable from the equation.
Example 6
A crane does 680 J of work as it lifts a crate a height of 20.0 m. What is the mass of the crate?
Given: W = 680 J d = 20.0 m g = 9.81 m/s2 θ = 0°
Find: m
Formula: W= mgd cos θ
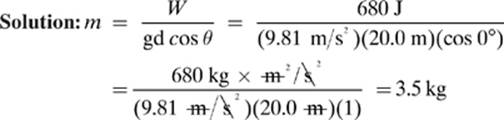
Of course, we wouldn”t need a crane to pick up the crate from Example 6. A kilogram weighs only about 2.2 pounds near the surface of Earth, so the “crate” weighs only about
![]()
Now go on to the review questions.
Lesson 3–1 Review
1. _______________ is the product of the displacement and the component of the force in the direction of the displacement.
2. A boy drags a sled 12.0 m across the snow by exerting a 20.0 N force along a rope at an angle of 55.0° above the horizontal. How much work does the boy do on the sled?
3. A worker does 350 J of work lifting a 15.0 kg item to a shelf. How high does she lift it?
4. A man holds a 50.0 kg weight stationary above his head, at a height of 1.90 m, for a period of 15.0 seconds. How much work does he do during this period of time?
5. A waitress walks at a uniform speed, covering 4.0 meters as she carries a 3.0 kg tray at a constant height 1.50 m. How much work does she do on the tray during this period of time?