Homework Helpers: Physics
3 Work, Energy, Power, and Momentum
Lesson 3–3: Conservation of Energy
One of the most important laws of physics is the law of conservation of mechanical energy, which states that in the absence of dissipative forces (such as friction), the total amount of mechanical energy in a system is conserved. In physics we define mechanical energy as the sum of the kinetic energy and all forms of potential energy in a system. When an object falls, its gravitational potential energy is converted into kinetic energy, but the total mechanical energy (when we ignore friction) remains the same. It may seem strange to you that we are ignoring friction once again. If we did a problem where an object was falling from such a great height that it reached terminal velocity, it certainly would be inappropriate to ignore friction, because the object would clearly be losing gravitational potential energy without gaining more kinetic energy. However, the problems that we will be dealing with involve small falls and therefore insignificant losses due to friction.
Example 1
A 5.4 kg bowling ball falls from rest off a shelf at a height of 1.2 m. Calculate both the gravitational potential energy of the ball with respect to the floor and the kinetic energy of the ball (a) just before it falls, when its height is 1.2 m; (b) when it is falling and its height is 0.60 m; and (c) the instant before the ball hits the ground, when its height would round to 0.0 m above the ground.
This represents a classic problem used to show conservation of mechanical energy.
a) At a height of 1.2 m
When the ball is at its maximum height, its gravitational potential energy will be
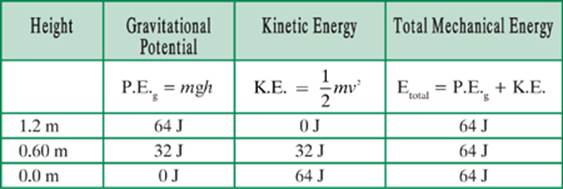
P.E.g = mgh = (5.4 kg)(9.81 m/s2)(1.2 m) = 64 J
Because the ball hasn”t started falling at this point, its velocity is zero, and its kinetic energy will be equal to
![]()
The total of these two forms of energy must remain the same for each part of the problem.
![]()
Knowing this will save us a good deal of work while solving the rest of the problem.
b) At a height of 0.60 m
When the ball has fallen halfway and its height has decreased to 0.60 m, its gravitational potential energy will be
P.E.g = mgh = (5.4 kg)(9.81 m/s2)(0.60 m) = 32 J.
We can easily find the kinetic energy at this height because the total mechanical energy must be conserved.
K.E. = Etotal – P.E.g = 64 J – 32 J = 32 J
If we didn”t know this relationship, we would have to use a formula for free fall to find the velocity of the bowling ball at this height, as shown here:
![]()
*I kept an extra digit in my answer to velocity to avoid a rounded answer in the kinetic energy that would look slightly different than the kinetic energy.
Using this velocity, we could find the kinetic energy of the bowling ball at 0.60 m.
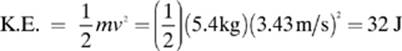
Just looking at the formula for velocity and substituting it into our formula for kinetic energy, you can see that it will be equal to our formula for gravitational potential energy.
![]()
c) At a height of 0.0 m
Finally, we can find the gravitational potential energy and the kinetic energy of the bowling ball the instant before it hits the ground. The key here is to remember that the bowling ball is still moving (velocity is not zero) but the height is essentially zero, right before it strikes the ground. At this point, all of the original gravitational potential energy has been converted to kinetic energy.
P.E.g = mgh = (5.4 kg)(9.81 m/s2)(0.0 m) = 0 J
K.E. = Etotal – P.E.g = 64 J – 0 J = 64 J
It took us a long time to get here, but hopefully you see that these problems are actually quite easy. All you need to do is find the original gravitational potential energy and add or subtract from there. It may help to see the problem summarized in the following table.
The relationship between gravitational potential energy and kinetic energy can be used to solve another type of interesting problem, as shown in our next example.
Example 2
A child slides down a frictionless slide from a height of 1.8 m. How fast will she be going at the bottom of the slide?
Given: g = 9.81 m/s2 h = 1.8 m
Find: v
Now, this is where a novice student begins to panic. You need to find the speed of the child at the bottom of the slide, but you only have the height of the slide and the value of g. You can”t think of any formula that will allow you to solve for velocity with only this given information. However, if you remember that the kinetic energy that the child gains is equal to the gravitational potential energy that he or she loses, you can set the two equations equal to each other and solve for velocity.

This example reminds us that we don”t need to know the mass of an object to determine its final velocity, as the speed of a falling object is not dependent upon its mass.
Lesson 3–3 Review
1. A box with a mass of 12.0 kg slides down a frictionless slide with a height of 3.00 m. What will be the kinetic energy of the box at the bottom of the ramp?
2. An apple with a mass of 0.10 kg falls off a tree branch with a height of 2.75 m. Find the velocity of the apple as it hits the ground.
3. A bowling ball with a mass of 5.00 kg falls off a shelf with a height of 2.00 m. How much kinetic energy would the bowling ball have when it has fallen halfway to the floor, when its height is 1.00 m?