Homework Helpers: Physics

3 Work, Energy, Power, and Momentum

If you have ever been coached in a sport that involves striking a ball with some type of club, bat, or racket, you have probably been told about the importance of “follow-through.” Using tennis as an example, the purpose of follow-through is to increase the amount of time that the ball is in contact with the racket. Remember: The racket is what is applying the force to the tennis ball, so follow-through allows the force to be applied for a longer period of time, resulting in greater acceleration. In physics, the product of the force and the time for which the force is applied is calledimpulse. Impulse is typically represented with the symbol J and is measured in newtons × seconds (N × s).

J = FΔt

The impulse-momentum theorem states that the impulse applied to an object will result in a change in the object”s momentum, giving rise to the very useful formulas:

FΔt = Δp or FΔt = mΔv or FΔt = m(v_f – v_i)

Example 1

A golf club exerts a uniform force of 22.0 N on a golf ball for a period of 0.250 s. Calculate the change in the ball”s momentum.

Given: F = 22.0 N Δt = 0.250 s

Find: Δp

Solution:

Δp = FΔt = (22.0 N)(0.250 s) = (22.0 kg · m/s²)(0.250 s) = 5.50 kg · m/s

Example 2

A girl playing T-ball hits a 0.20 kg baseball off a tee, exerting a force of 3.5 N for a period of 0.15 s. Find the final velocity of the baseball.

Given: F = 3.5 N m = 0.20 kg Δt = 0.15 s v_i = 0.0 m/s

Find: v_f

If we rearrange the impulse formula and isolate the force, we can see how it relates to many real-life situations.

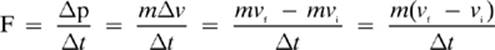
Notice that the instantaneous force that an object experiences is inversely proportional to the amount of time that the force acts. That means that if it takes longer for an object to come to a stop, it will experience a smaller instantaneous force. When a glass drops on a rug, the rug increases the stopping time, preventing the glass from breaking. When you catch a baseball with a glove, you probably move the glove back as you catch the ball, increasing the stopping time and decreasing the instantaneous force.

Example 3

A boy catches a 0.10 kg baseball with an initial velocity of 12.0 m/s, bringing it to rest in 0.89 s. Calculate the average force exerted on the ball during the period it was being brought to rest.

Given: m = 0.10 g v_i = 12.0 m/s v_f = 0.0 m/s Δt = 0.89 s

Find: F

Don”t be surprised by the negative sign in our answer, which simply indicates that the boy must exert a force in the opposite direction to stop the ball.

Lesson 3–6 Review

1. _______________ is the product of a force and the time interval during which the force acts.

2. Calculate the impulse of a 20.0 N force acting for 15.0 s.

3. A 0.100 kg puck has an initial velocity of 3.50 m/s until a player hits it with a stick, exerting a force of 12.0 N in the direction of its motion for 0.344 seconds. What is the final velocity of the puck?