Homework Helpers: Physics
4 Rotational and Circular Motion
Lesson 4–4: Centripetal Force and Centripetal Acceleration
One more time, let”s draw upon a fairly common experience and refer back to the days when you rode the merry-go-round at the park. When you first got on the ride it was stationary. It had an angular velocity of zero, and you, once you got seated, had a tangential velocity of zero. Then someone, perhaps a parent or an older sibling, started rotating the merry-go-round. You shouted, “Faster!” and he or she increased his or her efforts, increasing the angular velocity of the ride, and, as a result, increased your tangential velocity. Let”s suppose the person eventually got the merry-go-round rotating as fast as he or she could make it go, and maintained that angular velocity for a long period of time. Would your tangential velocity keep changing? Of course it would!
This goes back to the “trick” question we discussed in Lesson 1–2, when we described velocity as “speed in a particular direction.” Velocity includes both speed and direction, and as you go around the merry-go-round, the direction of your tangential velocity keeps changing. This means that even if the speed, frequency, and period of the ride remain the same, your tangential velocity is constantly changing as you change direction. Notice how the direction of the velocity vector keeps changing in Figure 4.4.
The child”s velocity keeps changing, so the child, by definition, is accelerating.
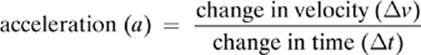
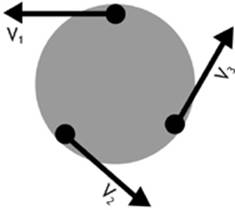
Figure 4.4
Newton”s second law tells us that this acceleration is evidence of an unbalanced force acting on the child.
Force = mass × acceleration
What is the source of this mysterious force and in what direction is it acting?
Can you imagine what would happen to a boy sitting on a merry-go-round if the friction between him and the ride was suddenly reduced to zero? The child”s own inertia would cause him to fly off in the direction of his velocity at the instant that the ride became frictionless. Assuming that the boy is not holding on, it is only the force of friction between him and the ride that overcomes his inertia and changes his velocity. The force of friction and the acceleration experienced by the child are directed toward the center of rotation. We call this type of force and accelerationcentripetal, or “center-seeking.”
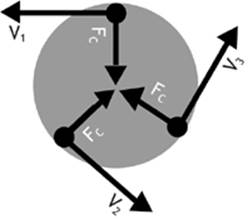
Figure 4.5
Centripetal Acceleration
An acceleration directed toward the center of a circular path.
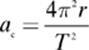
Centripetal Force
A force directed toward the center of a circular path.
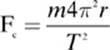
Example 1
A 35.0 kg boy sits on a merry-go-round with a period of 3.78 s at a distance of 175 cm from the center of rotation. Find the boy”s tangential speed, and the centripetal acceleration and centripetal force he experiences.

There will be times when you know the angular velocity of the object and you will need to calculate the centripetal acceleration and/or force the object experiences. In these cases you will want to recall one of the formulas from our previous lesson: v = rω.
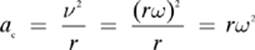
Example 2
A boy spins a 355 g ball on the end of a string with a length of 45.7 cm in a uniform horizontal circle above his head. The angular speed of the ball is 8.76 rad/s. Find the centripetal acceleration and tension in the string.
When the problem asks for the tension in the string, it is really asking for the centripetal force on the ball. The string is what provides the centripetal force in this example.
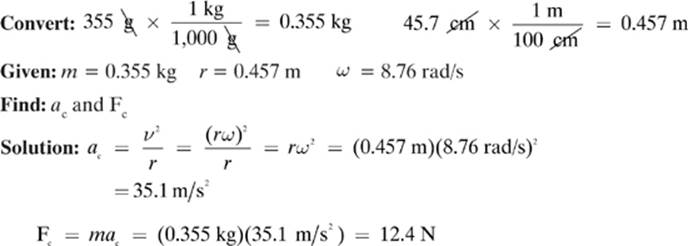
Lesson 4–4 Review
1. ________________ is a force directed toward the center of a circular path.
2. Calculate the centripetal force that keeps a 65.0 kg object in a circular path with a centripetal acceleration of 23.5 m/s2.
3. At what radius would an object in circular motion with a centripetal acceleration of 5.32 m/s2 have a tangential speed of 22.4 m/s?