Homework Helpers: Physics
5 Electric Charges, Forces, and Fields
Answer Key
The actual answers will be shown in brackets, followed by an explanation. If you don”t understand an explanation that is given in this section, you may want to go back and review the lesson that the question came from.
Lesson 5–1 Review
1. [A proton]—the proton has a charge that is equal in magnitude to the charge on an electron, but with an opposite sign.
2. [a negative ion]—A negative ion has gained additional negative charges, giving it a net charge that is negative.
3. [–3.20 × 10–19 C]—We simply multiply 2 by the charge on 1 electron.
![]()
Lesson 5–2 Review
1. ![]()
2. [The force would be quadrupled.]—Doubling the charge on each object would cause the product of the charges to be multiplied by a factor of (2 × 2) 4.
3. [The force would be 1/4th as great.]—Because the force is inversely proportional to the square of the distance between the two objects, doubling the distance will cause the force to be divided by a factor of (22) 4.
Lesson 5–3 Review
1. [Conduction]—It may help to remember the letter c in both conduction and contact.
2. [Grounding]—Grounding a charged object will eliminate the excess charge and make it neutral.
3. [Polarization]—When you bring a charged balloon close to a neutral wall, the wall becomes polarized, as the electrons near the surface of the wall are repelled by the excess electrons on the balloon.
4. [No]—If you bring a charged object with sufficient charge near a neutral electroscope, it will react, but it will react the same way to a positive or a negative object. If the object is charged negative, it will repel electrons from the knob into the vanes. The vanes will both become negatively charged and repel each other. If the object is charged positive it will draw electrons up from the vanes into the knob. The vanes will both become positively charged and repel each other.
Lesson 5–4 Review
1. [The forces would be equal in magnitude, but opposite in direction.]—The formula F = qE shows that the force experienced by a particle will be directly proportional to its charge. The proton and electron have equal but opposite charges, so the forces that they experience will be equal and opposite as well.
2. [6.9 N/C]—As long as you know the charge on an electron, –1.60 × 10–19 C, the rest is easy.
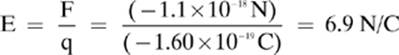
3. 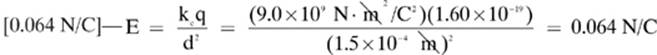
4. [7.0 × 10–19 N]—Remember: The helium (He2+) ion has two additional protons, giving it a charge of
q = ne = 2(+1.60 × 10–19 C) = +3.20 × 10–19 C.
Solving for the electrostatic force it experiences in an electric field we get
F = qE = (+3.20 × 10–19![]() )(2.2 N/
)(2.2 N/![]() ) = +7.0 × 10–19 N. The question only asked for the magnitude of the force, so the sign indicating direction isn”t necessary.
) = +7.0 × 10–19 N. The question only asked for the magnitude of the force, so the sign indicating direction isn”t necessary.
Lesson 5–5 Review
1. [Electric potential energy]—For point charges, we can find the electric potential energy with the formula: ![]() . For charged plates, we use: ΔP.E.electric = –qEd.
. For charged plates, we use: ΔP.E.electric = –qEd.
2. 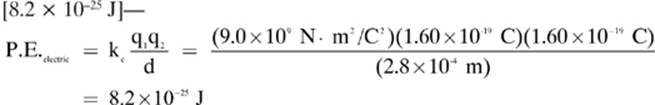
Lesson 5–6 Review
1. [Electron volt]—Although this term includes the word “volt”, it is really a unit of energy. The conversion between electron volts and joules is: 1 eV = 1.6 × 10–19 J.
2. [4.5 eV]—One proton has the same charge as one electron, so we will use 1.00 e as the value for q.
ΔP.E.electric = qΔV=(1.00e)(4.5V) = 4.5 eV
3. 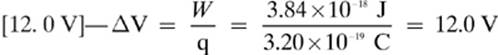
Lesson 5–7 Review
1. [The capacitance will decrease]—The capacitance of a capacitor is inversely proportional to the distance between its plates, as shown by the formula:
![]()
2. [1.8 × 10–7 f]—Remember to change 1.6 µC into 1.6 × 10–6 C, and then solve:
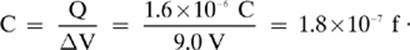
3. [7.5 × 10–6 J]—Remember to convert 2.5 µC to 2.5 × 10–6 C. Then solve:
![]()
Chapter 5 Examination
1. [h. capacitor]—An electroscope is a device that can become charged, but it doesn”t store the charge.
2. [b. induction]—The process of induction produces a charged object with a charge that is the opposite to the original charged object.
3. [e. negative ion]—Remember: It has gained additional negative charges (electrons), giving it a net negative charge.
4. [i. electric potential]—Voltage is the difference in electric potential between two points.
5. [g. grounding]—Lightning rods are based on this principle.
6. [a. protons and electrons]—If an atom has the same number of positive and negative charges, the net charge is zero.
7. 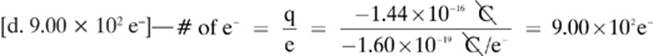
8. [b. 11]—Remember: The excess electrons repel each other, so they will move to maximize the distance between them. The spheres are metal, so the electrons are free to spread out. The spheres are identical, so they will be evenly distributed over the surface of both spheres, resulting in the same number of excess electrons on each sphere.
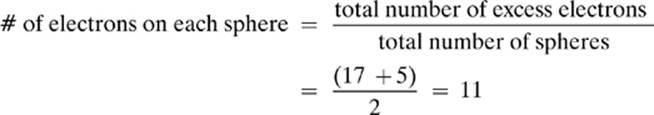
9. [d. 9F]—Coulomb”s law tells us that the electrostatic force between two charged objects is directly proportional to the product of the charges, as shown by ![]() . If the charge on each object was tripled, the product of the charges would increase by a factor of (3 × 3) 9, giving us 9 × F.
. If the charge on each object was tripled, the product of the charges would increase by a factor of (3 × 3) 9, giving us 9 × F.
10. ![]() —Coulomb”s law tells us that the electrostatic force between two charged objects is inversely proportional to the square of the distance between them, as shown by the equation
—Coulomb”s law tells us that the electrostatic force between two charged objects is inversely proportional to the square of the distance between them, as shown by the equation ![]() . If the distance between the objects was increased from 1.0 cm to 5.0 cm, it was increased by a factor of 5. That means that the electrostatic force between the objects would decrease by a factor of 52 = 25.
. If the distance between the objects was increased from 1.0 cm to 5.0 cm, it was increased by a factor of 5. That means that the electrostatic force between the objects would decrease by a factor of 52 = 25.
11. [b. 5.60 × 10–14 N]—You will need to recall that the charge on an electron is –1.60 × 10–19 C. Notice that we can figure out what operation to carry out by looking at the units, even if we couldn”t recall the proper formula. The question asks for a force, which is measured in newtons, and we have one given (field intensity) measured in N/C and another given measured in C. The only way to get the coulombs to cross out is to multiply our givens together. N/![]() ×
× ![]() = N. Of course, it is always better to look up the formula, if you have the opportunity.
= N. Of course, it is always better to look up the formula, if you have the opportunity.
![]()
The question asks only for the magnitude of the force, so that is why we leave the negative sign off our final answer.
12. 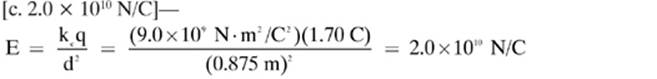
13. 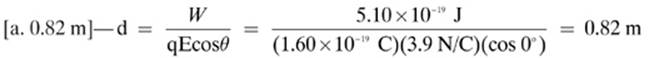
14. 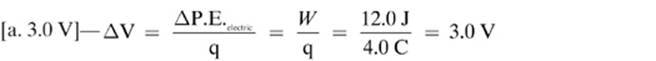
15. 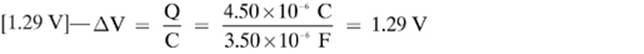
16. 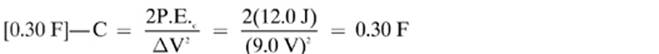
17. 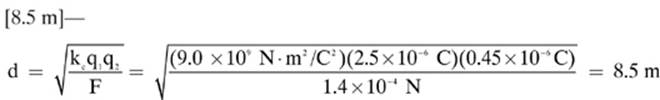
18. [3.8 × 1019 N/C]—To solve this, recall that the charge on an electron is 1.60 × 10–19 C.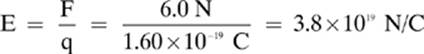
19. [36 J]—W = ΔP.E. = qΔV = (4.0 C)(9.0 V) = 36 J
20. [1.28 × 10–18 C]—q = ne = 8(+1.60 × 10–19 C) = +1.28 × 10–18 C