Homework Helpers: Physics
6 Electric Current and Circuits
Answer Key
The actual answers will be shown in brackets, followed by an explanation. If you don”t understand an explanation that is given in this section, you may want to go back and review the lesson that the question came from.
Lesson 6–1 Review
1. [Direct current]—Batteries and cells, like the ones that we use in flashlights, provide direct current.
2. [110 C]—q = IΔt = (2.0 A)(55.0 s) = 110 C
3. 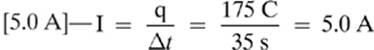
4. [Counter-clockwise]—Conventional current flows from positive to negative, which is the opposite of the direction of electron flow, which goes from negative to positive.
Lesson 6–2 Review
1. [Resistance]—Given the potential difference and current, we can calculate resistance with Ohm”s law:
![]()
2. 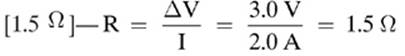
3. 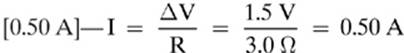
Lesson 6–3 Review
1. 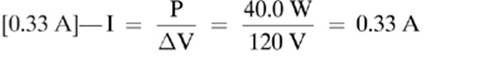
2. ![]()
3. 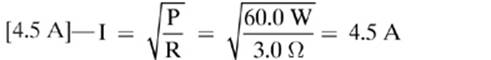
4. [40. W]—P = I2R = (0.50 A)2 (160Ω) = 40. W. The decimal point after the zero indicates that it is a significant digit.
5. [$0.11]—first, we must change watts to kilowatts by dividing by 1,000, or moving the decimal three places to the left. That gives us a power rating of 0.080 kilowatts.
Multiplying the power rating by the number of hours, we get 0.080 kW × 8.0 hours = 0.64 kW-h of energy.
Now, we are ready to solve using the formula
Cost = energy × rate = 0.64 kW-h × $0.17/kW-h = $0.11 or 11 cents.
Lesson 6–4 Review
1. [0.56 A]—You should recall that in a series circuit, there is only one value for current, as shown in the formula Is = I1 = I2 = ... Ix. If we find the total current, that will be equal to the current through the 5.0Ω resistor. First, we will find the total resistance.
Rs = R1 + R2 + R3 = 2.0Ω + 5.0Ω + 9.0Ω = 16.0Ω
Then, we will use Ohm”s law to find the current.
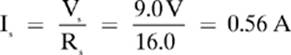
2. [9.0 µf]—Cp = C1 + C2 = 2.0 μf + 7.0 μf = 9.0 μf
3. [10.3 W]—There are several different formulas for electric power, so there are several different ways to go about solving this problem. You might follow the procedure that I demonstrated with the example problem, where I found the total resistance for the circuit, so that I could calculate the current through each branch of the circuit. However, the easiest way to solve this problem is to select the formula for electric power that doesn”t require you to know the current through the resistor.
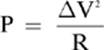
To solve this problem, all you need to remember is that in a parallel circuit, the voltage across each resistor is the same as the voltage of the battery. So,
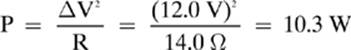
It should be noted that if you solved this problem with different formulas, there could be a slight difference due to rounding.
Chapter 6 Examination
1. [e. alternating current]—In the United States, household current reverses itself 120 times per second, for a total of 60 cycles/second.
2. [d. conventional current]—Although the electrons in a particular circuit may flow clockwise, the convention current would be in the opposite direction, counterclockwise.
3. [b. circuit]—A complete circuit is required for current to flow.
4. [g. electric power]—A 60-watt bulb converts 60 joules of energy per second.
5. [c. resistance]—Not to be mistaken with resistivity, which is a proportionality constant.
6. [c. ohms]—The symbol for ohms is the Greek letter (Ω) omega.
7. [d. watts]—The symbol for watts is W.
8. [b. potential difference]—Voltage is another term for potential difference.
9. [a. 270 C]—q = IΔt = (3.0 A)(90.0 s) = 270 C
10. 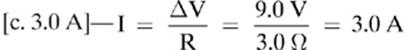
11. [b. 13.0Ω]—Rs = R1 + R2 + R3 = 2.0Ω + 4.0Ω + 7.0Ω = 13.0Ω
12. [c. 9.0 V]—In a parallel circuit, the potential difference across each component is the same as the source. Vp = V1 = V2 = V3
13. [d. 28 W]—P = I2R = (2.0 A)2(7.0Ω) = 28 W
14. 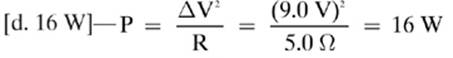
15. 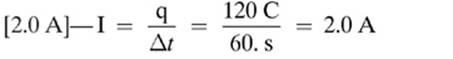
16. 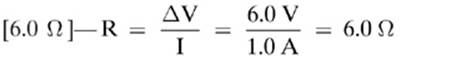
17. 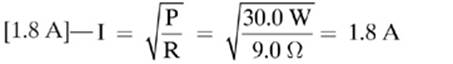
18. 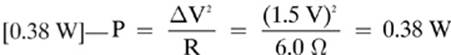
19. [1.2 V]—We can solve this problem with Ohm”s law, V = IR, provided we find the total current through the resistor. In order to do that, we need to find the total resistance, and divide that into the total potential difference.
Rs = R1 + R2 + R3 = 5.0Ω + 9.0Ω + 12.0Ω = 26.0 ©
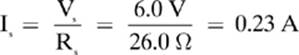
Remember that in a series circuit, the total current is the same as the current through each of the component, so (Is = I1 = I2 = I3 = 0.23 A) the current through the 5.0 DΩ resistor is 0.23 A. Our final answer can be determined.
V1 = Is R1 = (0.23 A)(5.0Ω) = 1.2 V
20. [$0.034, or 3.4 cents]—To solve this problem, you will need the power rating for the fan, which can be calculated as
P = IΔV = (0.55 A)(120 V) = 66 W
Next, I will want to convert this to kW.
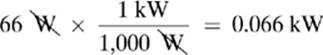
Now, I will calculate how many kilowatt-hours (kW-h) I use when operating this fan for 3.00 hours: 0.066 kW × 3.00 hours = 0.20 kW-h.
Finally, I multiply the number of kilowatt-hours by the rate to find the cost.
C = ER = (0.20 kW-h)($0.17/kW-h) = $0.034
So, it costs 3.4 cents to run this fan for 3.00 hours.