Homework Helpers: Physics
10 Nuclear Physics
Lesson 10–2: Plank”s Photons
As we discussed in Chapter 8, the particle theory of light was dealt a devastating blow by the double-slit experiment carried out by Thomas Young in the beginning of the 19th century. We also learned that Albert Einstein was able to provide new evidence for the particle theory of light in 1905, when he used the idea of photons of light to explain the photoelectric effect. What we haven”t discussed yet is the fact that Einstein applied the work of Max Planck (1858–1947) to his explanation.
Max Planck studied a particular problem involving blackbody radiation, which we don”t have room to really discuss here. In 1900 Planck developed a theory and formula that treated energy as if it were made up of discrete tiny packets called quanta, or photons. Different photons represent different amounts of energy, and the energy and frequency of the photons are proportional to each other.
E ∝ f
Planck introduced a proportionality constant (h), which sets the two sides of the equation equal to each other.
E = hf
Where Planck”s constant (h) has a value of 6.63 × 10–34 J · s.
It is now common practice to calculate the energy associated with the photons of a particular frequency of light, or other type of electromagnetic wave.
Example 1
Calculate the energy of a photon with a frequency of 4.5 × 10–7 Hz.
Remember: The unit we call hertz (Hz) is really a derived unit equivalent to the inverse second (s–1). To make it more obvious how the units cross out, I will substitute s–1 for Hz in our calculation.
Given: f = 4.50 × 10–7 Hz h = 6.63 × 10–34 J · s
Find: E
![]()
The relationship between the frequency and wavelength of an electromagnetic wave was presented in a formula in Chapter 8:
C = fλ
Solving for frequency, we get:
![]()
If we substitute this value for frequency into Planck”s equation, we get:
![]()
Example 2
How much energy does a photon with a wavelength of 3.50 × 10–8 m contain?
Recall that the speed of light in a vacuum (C) is 3.00 × 108 m/s.
Given: λ = 3.50 × 10-8 m h = 6.63 × 10-34 J · s C = 3.00 × 108 m/s
Find: E
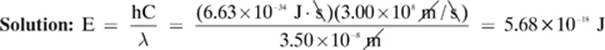
The amount of energy represented by our answers to examples 1 and 2 is so tiny that it is common to ask for the answers to this type of question in electron volts (eV), which we discussed in Chapter 5. Recall that one electron volt is the amount of energy required to move the charge of one electron across a potential difference of one volt. Our conversion factor from Chapter 5 is: 1e V = 1.60 × 10-19 J. This gives us a value for Planck”s constant of
![]()
Example 3
Calculate the wavelength of a photon of light with an energy of 2.1 eV.
Given: C = 3.00 × 108 m/s h = 4.14 × 10-15eV · s E = 2.1eV
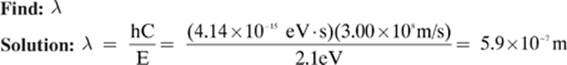
The Momentum of a Photon
Although we often think of light as being made up of waves, as suggested by Thomas Young”s double-slit experiment, other experiments have been designed to study the particle-like properties of light. One particle-like property associated with photons, momentum, can be determined with the following formula:

or
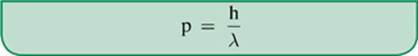
Example 4
Calculate the momentum of a photon with a wavelength of 4.90 × 10–6 m.
Given: λ = 4.90 × 10-6 m h = 6.63 × 10-34 J · s
Find: p
![]()
Wave-Particle Duality
As the particle-like properties of light and other electromagnetic waves were being established, Louis de Broglie (1892–1987) suggested that perhaps particles also had wave-like properties. It has since been verified that the wavelength of a particle can be determined with the formula:
![]()
Example 5
Calculate the wavelength of an electron with a velocity of 4.5 × 107 m/s.
Given: m = 9.109 × 10–31 kg v = 4.5 × 107 m/s h = 6.63 × 10–34 J · s

So, it is not just light that exhibits wave-particle duality. All things can be treated as both waves and particles. However, as you can see in the previous formula, the wavelength of a particle is inversely proportional to its mass. The masses of the objects in our macroscopic world are large enough to render their wave-like properties insignificant. Significant wave-like properties are only detectable in particles with very tiny masses.
Lesson 10–2 Review
1. Calculate the energy associated with a photon with a wavelength of 3.7 × 10–6 m.
2. Calculate the wavelength of a proton with a velocity of 2.54 × 105 m/s.
3. Calculate the momentum of a photon with a wavelength of 7.6 × 10–4 m.