Homework Helpers: Physics

1 Kinematics

Most of us became familiar with projectile motion long before we studied physics. Playing catch in the backyard, we observed the motion of a ball as we tossed it to our friend. The ball”s path formed a parabola. As the ball came back to us, we saw it rise until it reached its maximum height, and then it started to come down, moving toward us the entire time. The ball would be considered a projectile because after you release it, the only force acting upon it (if we ignore air resistance) is gravity. Other common projectiles would include bullets, arrows, snowballs, cannonballs, and basketballs. The motion of such objects is appropriately called projectile motion.

Up to this point, we have only considered motion that takes place along one dimension at a time. We talked about objects falling downward, or objects moving forward, but not both at the same time. We know from real-life experiences that objects often do fall downward along what we might call the y-axis, while moving forward along what can be called the x-axis, but until now, we weren”t ready to study motion along both dimensions at the same time. Now we should be ready. The truth is: If you are careful with your problem-solving, projectile motion problems aren”t much harder than the problems we studied in Lesson 1–4.

Horizontal Projectile Motion

The first type of projectile motion that we will consider is often called horizontal projectile motion, because all of the projectile”s initial velocity will be directed along the horizontal, or x-axis. This is the type of motion that you see when an object rolls off the edge of a table, or when a ball is launched parallel to the ground. As you might imagine, an object can have an initial velocity of zero in the vertical (y), even when it has a nonzero initial velocity in the horizontal (x). It is also interesting to note that the acceleration in the horizontal (x) dimension is zero, when we ignore air resistance, but the acceleration in the vertical (y) will be equal to the acceleration due to gravity (g), assuming the projectile is launched near the surface of Earth. Let”s try an example of a problem and go through the steps involved in the solution.

Example 1

A marble rolls off the edge of a table with a height of 0.755 m and strikes the floor at a distance of 24.3 cm from the edge of the table. Calculate the initial velocity of the ball. (Ignore air resistance.)

These problems are often called two-dimensional motion problems, and we study the motion in each dimension separately. It is a good practice to list the “givens” for the x and y dimensions separately, and label everything carefully. For example, v_iy will indicate the initial velocity in the y dimension, and d_x will indicate the displacement in the horizontal dimension.

Convert: The horizontal displacement was given in cm. Let”s convert this value to m so that it will match the vertical displacement.

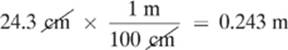
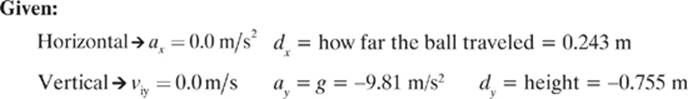
Find: v_ix

We gave the acceleration in the y (a_y or g) and the displacement in the y (d_y) negative signs because they are both directed downwards.

We need to find the initial velocity of the marble in the horizontal. Remember: We define velocity as the rate of displacement, as shown by the formula . Because there is no acceleration in the x dimension, we can safely assume that the initial horizontal velocity of the marble is the same as the average velocity in the horizontal, so we can solve for our unknown using the formula .

We already know that the displacement in the horizontal dimension is 0.243 m, because that is how far the ball landed from the edge of the table. All that we need to do is to determine the amount of time that the ball was in the air. How do we do that? We know the initial velocity of the ball in the y was zero. We also know the height from which the ball fell, and the acceleration due to gravity, so we simply do a free-fall problem.

Armed with both the displacement in the horizontal and the change in time, we can solve for the initial velocity in the horizontal, as shown here:

Notice that I rounded the answer to three significant digits, because the original values in the problem contained three significant digits.

Let”s try another example of a horizontal projectile motion, but this time, let”s solve for a different unknown. Once again, you should notice that mechanical problem-solving won”t be enough to do these types of problems. You must approach each problem that you encounter ready to reason out a solution.

Example 2

An archer stands on the wall of a castle and fires an arrow from a height of 12.10 m above the ground. A level field stretches out in front of the castle wall as far as the eye can see. If the archer fires an arrow parallel to the ground with an initial horizontal velocity of 11.0 m/s, how far will the arrow travel horizontally before hitting the ground? (Ignore air resistance.)

Given:

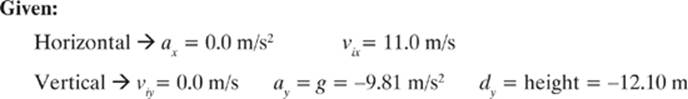
Find: d_x

First, we will find out how long the arrow will be in the air using the distance that the arrow must fall to hit the ground with the formula that we found for the previous problem.

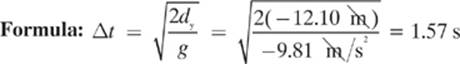
Next, we make use of the initial velocity (v_ix) in the horizontal and the change in time (Δt) to find the displacement.

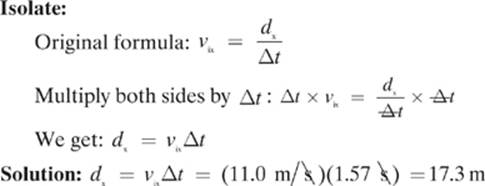
Let”s try one more example of a horizontal motion before moving on to the next type of projectile motion problem.

Example 3

An airplane is flying a practice bombing run by dropping bombs on an old shed. The plane is flying horizontally with a speed of 185 m/s. It releases a bomb when it is 593 m away from the shed, and it scores a direct hit. Assuming there is no air resistance, how high was the airplane flying when it dropped the bomb?

You might not recognize this as an example of horizontal projectile motion at first, but the bomb is being dropped while it is moving forward with the same speed as the plane, and it experiences free fall on its way down. You might have noticed that I used the word speed instead ofvelocity in this problem, but that it just because I didn”t specify the direction or heading of the plane. I could have also said that the magnitude of the velocity is 185 m/s. Either way, we solve the problem the same way.

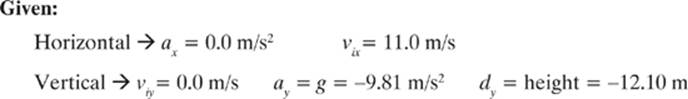
Find: d_y

Can you see where you should begin to solve this problem? We will start by using the initial horizontal velocity and the horizontal displacement to determine how long the bomb was in the air, or Δt.

Now that we know how long it takes the bomb to fall, we can calculate the bomb”s vertical displacement, as shown.

The negative sign simply indicates that the bomb fell downward. We won”t include the negative sign in our final answer, because we were solving for the altitude of the plane, not the displacement of the bomb.

Answer: The plane was flying at a height of 50.5 m.

Parabolic Motion

Let”s move on to the other major type of projectile motion problem, which is sometimes called a parabolic motion problem because of the shape of the paths these objects take. In this type of problem, a projectile is given an initial velocity in two dimensions, so we need to go over a technique for dealing with our initial velocity vectors. Our first task in this type of problem will often be to take the initial velocity vector and resolve it, or break it up, into horizontal and vertical components. Once we have the component velocity vectors, we can add them to our list of “givens.”

Resolution of Vectors

Breaking an individual vector up into two or more component vectors.

By now, you should be getting the hang of vector addition, so I would like to add another tool to your mental toolbox. To do parabolic motion problems, you need to be able to break a vector apart into its individual components, rather than adding components to find a resultant vector. Let”s imagine that a cannon is set up so the barrel points at an angle of 34.0° above the horizontal. When the cannon is fired, the ball launches with an initial velocity of 23.0 m/s at an angle of 34.0° above the ground. How could we figure out how fast the ball is moving upward, and how fast it is moving forward as it leaves the barrel of the cannon?

Draw a horizontal line to represent the ground, and add the initial velocity vector. Unless you plan on drawing everything to scale and using a protractor and a ruler to solve graphically, the diagram doesn”t need to be drawn to scale.

Now, if we draw a vertical line from the tip of the velocity arrow to the horizontal line representing the ground, so that this new line is perpendicular to the horizontal, we have a right triangle.

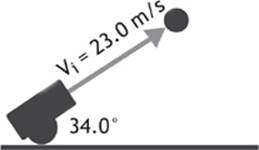
Figure 1.7

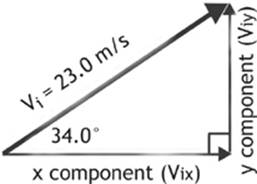
Figure 1.8

Notice how the initial velocity vector forms the hypotenuse of our right triangle. Turn the other sides of the triangle into arrows to represent the horizontal (x) and vertical (y) components of our initial velocity vector.

Remember that this is a right triangle, and we know all three angles and one side. This means that we can use trigonometry functions to find the magnitude of the remaining two sides.

Trigonometry Functions

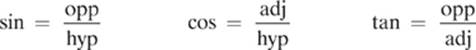
v_iy = opposite side = hypotenuse × sin θ = (23.0 m/s)(sin 34.0°) = 12.9 m/s

v_ix = adjacent side = hypotenuse × cos θ = (23.0 m/s)(cos 34.0°) = 19.1 m/s

Now that we have the horizontal (x) and vertical (y) components of the initial velocity, we can use this information to figure out how long the ball will be in the air (Δt), how high the ball will go (max d_y), and how far the ball will travel (d_x). Let”s put the entire problem together in a format similar to what you are likely to encounter.

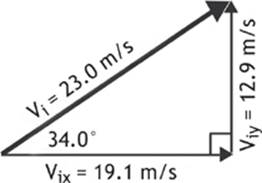
Figure 1.9

Example 4

A boy kicks a soccer ball, giving it an initial velocity of 7.50 m/s at an angle of 27.0° above the horizontal. How high will the ball go? How long will it be in the air? How far will it travel?

Before we even list our givens, let”s resolve the original velocity vector into its x and y components, just as we did with the cannonball.

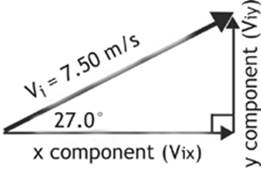
Figure 1.10

Resolution:

v_iy = v_i sin θ = (7.50 m/s)(sin 27.0°) = 3.40m/s

v_ix = v_i cos θ = (7.50 m/s)(cos 27.0°) = 6.68m/s

I also want to remind you of an “implied given” that we can make use of in this problem. The soccer ball will slow down as it goes upward, until its velocity in the y-dimension reaches zero at its maximum height (max d_y). Remember: The ball will continue to move forward, as it still has velocity in the x-dimension, but it stops going upward at the highest point in its flight. We can use this concept to help us find out how high the ball will go, and how long it will be in the air.

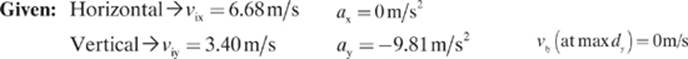
Find: Maximum height (d_y) Time of flight (Δt) Distance traveled (d_x)

Maximum Height

Time of Flight

We will figure out how long it takes the ball to travel to its maximum height and then double that change it time, because the ball will spend an equal amount of time falling from that height.

But, remember: This represents the change in time for the upward motion of the ball only! In order to find the total change, we must multiply this value by 2.

Total Δt = 2 × 0.347 s = 0.694 s

Distance Traveled

Lesson 1–7 Review

1. When we do projectile motion problems, what value do we use for acceleration in the x dimension?

2. If one bullet was fired horizontally from a height of 2.00 m and another was dropped from the same height at exactly the same time, which would hit the ground first? (Ignore air resistance, and assume a level horizontal field for the first bullet to travel along until it fell to the ground.)

3. If a football is kicked with an initial velocity of 12.0 m/s at an angle of 33.0° above the horizontal, what is the initial velocity in the y dimension?