SAT Physics Subject Test
Chapter 17 Solutions to the Chapter Review Questions
CHAPTER 2 REVIEW QUESTIONS
1 A Traveling once around a circular path means that the final position coincides with the initial position. Therefore, the displacement is zero. The average speed, which is total distance traveled divided by elapsed time, cannot be zero. And since the velocity changed (because its direction changed), there was a nonzero acceleration. Therefore, only I is true.
2 C By definition,
= ∆v / ∆t. We determine ∆v = v2 – v1 = v2 + (–v1) geometrically as follows:
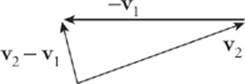
Since ∆t is a positive scalar, the direction of is the same as the direction of ∆v, which is displayed above; C is best.
3 C I is false since a projectile experiencing only the constant acceleration due to gravity can travel in a parabolic trajectory. II is true: Zero acceleration means no change in speed (or direction). III is false: An object whose speed remains constant but whose velocity vector is changing direction is accelerating.
4 C The baseball is still under the influence of Earth’s gravity. Its acceleration throughout the entire flight is constant, equal to g downward.
5 A Use Big Five #2 with v0 = 0.
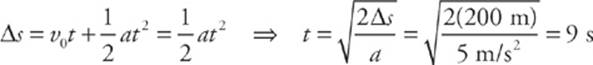
6 D Use Big Five #5 with v0 = 0 (calling down the positive direction).
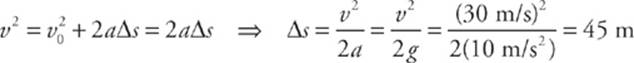
7 B First we determine the time required for the ball to reach the top of its parabolic trajectory (which is the time required for the vertical velocity to drop to zero).
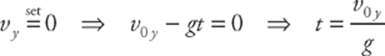
The total flight time is equal to twice the following value:
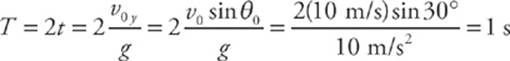
8 C After 4 seconds, the stone’s vertical speed has changed by ∆vy = ayt = (10 m/s2) (4 s) = 40 m/s. Since v0y = 0, the value of vy at t = 4 is 40 m/s. The horizontal speed does not change. Therefore, when the rock hits the water, its velocity has a horizontal component of 30 m/s and a vertical component of 40 m/s.
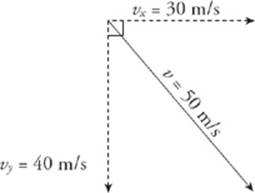
By the Pythagorean theorem, the magnitude of the total velocity, v, is 50 m/s.
9 E Since the acceleration of the projectile is always downward (because it’s gravitational acceleration), the vertical speed decreases as the projectile rises and increases as the projectile falls. A is false because the acceleration vector is straight down, but the velocity is never straight up or straight down. It would be true of the vertical component of the velocity, but not of the total velocity. B is false because the projectile still has its horizontal velocity at the top of the trajectory. C is false because the vertical component of the velocity changes, even if the horizontal component does not, so the total speed changes. D is false because the horizontal component is constant throughout the motion.
CHAPTER 3 REVIEW QUESTIONS
1 B Because the person is not accelerating, the net force he feels must be zero. Therefore, the magnitude of the upward normal force from the floor must balance that of the downward gravitational force. Although these two forces have equal magnitudes, they do not form an action/reaction pair because they both act on the same object (namely, the person). The forces in an action/reaction pair always act on different objects.
2 D First draw a free-body diagram.
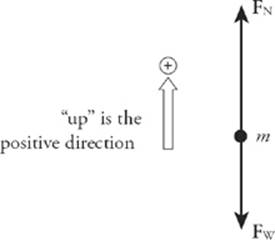
The person exerts a downward force on the scale, and the scale pushes up on the person with an equal (but opposite) force, FN. Thus, the scale reading is FN, the magnitude of the normal force. Since FN – Fw = ma, we have FN = Fw + ma = (800 N) + [800 N/(10 
)](5 m/s2) = 1200 N.
3 A The net force that the object feels on the inclined plane is mg sinθ, the component of the gravitational force that is parallel to the ramp. Since sin θ = (5 m)/(20 m) = 1/4, we have Fnet = (2 kg)(10 N/kg)(
) = 5 N.
4 C The net force on the block is F – Ff = F – μkFN = F –μkFw = (18 N) – (0.4)(20 N) = 10 N. Since Fnet = ma = (
)a, we find that 10 N = [
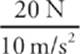]a, which gives a = 5 m/s2.
5 A The force pulling the block down the ramp is mg sinθ, and the maximum force of static friction is μsFN = μsmg cosθ. If mg sin θ is greater than μsmg cosθ, then there is a net force down the ramp, and the block will accelerate down. So, the question becomes, “Is sinθ greater than μscosθ?” Since θ = 30° and μs = 0.5, the answer is yes.
6 E One way to attack this question is to notice that if the two masses happen to be equal, that is, if M = m, then the blocks won’t accelerate (because their weights balance). The only expression given that becomes zero when M = m is the one given in E. If we draw a free-body diagram,
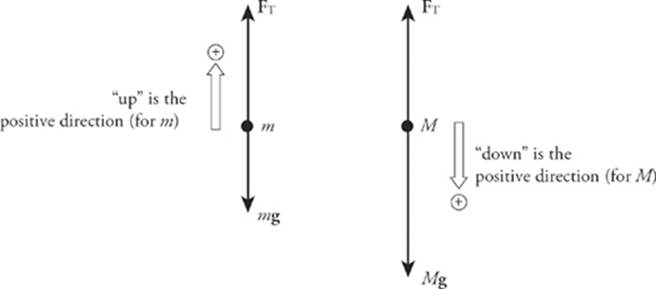
Newton’s second law gives us the following two equations:
FT – mg = ma (1)
Mg – FT = Ma (2)
Adding these equations yields Mg – mg = ma + Ma = (M + m)a, so
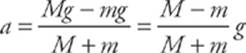
7 E If Fnet = 0, then a = 0. No acceleration means constant speed (possibly, but not necessarily, zero) with no change in direction. Therefore, B, C, and D are false, and A is not necessarily true.
8 D The horizontal motion across the frictionless tables is unaffected by (vertical) gravitational acceleration. It would take as much force to accelerate the block across the table on earth as it would on the moon. (If friction were taken into account, then the smaller weight of the block on the moon would imply a smaller normal force by the table and hence a smaller frictional force. Less force would be needed on the moon in this case.)
9 D The maximum force that static friction can exert on the crate is μsFN = μsFw = μs mg = (0.4)(100 kg)(10 N/kg) = 400 N. Since the force applied to the crate is only 344 N, static friction is able to apply that same magnitude of force on the crate, keeping it stationary. [B is incorrect because the static friction force is not the reaction force to F; both F and Ff (static) act on the same object (the crate) and therefore cannot form an action/reaction pair.]
10 A With crate #2 on top of crate #1, the force pushing downward on the floor is greater, so the normal force exerted by the floor on crate #1 is greater, which increases the friction force. B, C, D, and E are all false.
11 A Gravitational force obeys an inverse-square law: Fgrav ∝ 
. Therefore, if r increases by a factor of 2, then Fgrav decreases by a factor of 22 = 4.
12 E Mass is an intrinsic property of an object and does not change with location. This eliminates A and C. If an object’s height above the surface of the earth is equal to 2RE, then its distance from the center of the earth is 3RE. Thus, the object’s distance from the earth’s center increases by a factor of 3, so its weight decreases by a factor of 32 = 9.
13 C The gravitational force that the moon exerts on the planet is equal in magnitude to the gravitational force that the planet exerts on the moon (Newton’s third law).
14 D The gravitational acceleration at the surface of a planet of mass M and radius R is given by the equation g = GM/R2. Therefore
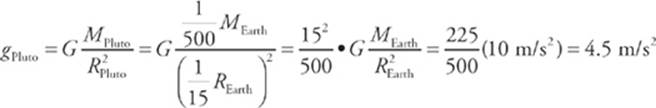
CHAPTER 4 REVIEW QUESTIONS
1 A Since the force F is perpendicular to the displacement, the work it does is zero.
2 B By the work–energy theorem
3 B Since the box (mass m) falls through a vertical distance of h, its gravitational potential energy decreases by mgh. The length of the ramp is irrelevant here.
4 C Since the centripetal force always points along a radius toward the center of the circle, and the velocity of the object is always tangent to the circle (and thus perpendicular to the radius), the work done by the centripetal force is zero. Alternatively, since the object’s speed remains constant, the work–energy theorem tells us that no work is being performed.
5 A The gravitational force points downward while the book’s displacement is upward. Therefore, the work done by gravity is –mgh = –(2 kg)(10 N/kg)(1.5 m) = –30 J.
6 D First, the kinetic energy the block gains is the same as the potential energy it loses, which is mgh. Since this is equal to 
mv2, we find that v = 
. Plugging in g = 10 m/s2 and h = 4 m, we get v = 
≈ 9 m/s.
7 C Apply conservation of mechanical energy (including the negative work done by Ff, the force of sliding friction).
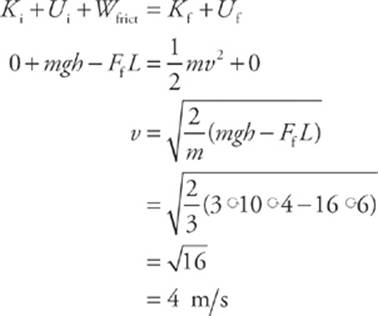
Note: Wtotal = ∆K could also be used.
8 E Apply conservation of mechanical energy (including the negative work done by Fr, the force of air resistance).
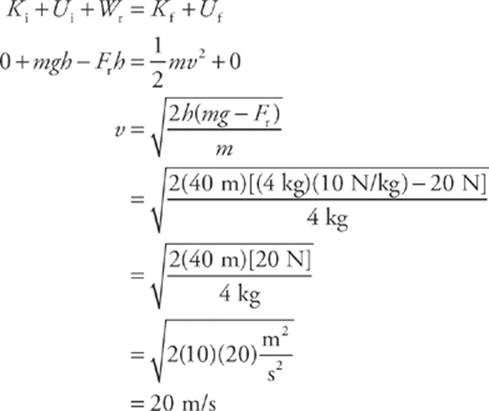
Again, Wtotal = ∆K could also be used.
9 E Because the rock has lost half of its gravitational potential energy, its kinetic energy at the halfway point is half of its kinetic energy at impact. Since K is proportional to v2, if Kat halfway point is equal to Kat impact, then the rock’s speed at the halfway point is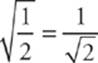 
its speed at impact.
10 D Using the equation P = Fv, we find that P = (200 N)(2 m/s) = 400 W.
11 D Apply conservation of mechanical energy.
CHAPTER 5 REVIEW QUESTIONS
1 C The magnitude of the object’s linear momentum is p = mv. If p = 6 kg · m/s and m = 2 kg, then v = 3 m/s. Therefore, the object’s kinetic energy is K = mv2 = (2 kg)(3 m/s)2 = 9 J.
2 C The impulse delivered to the ball, J = F∆t, equals its change in momentum. Since the ball started from rest, we have
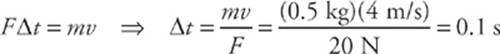
3 E The impulse delivered to the ball, J = 
∆t, equals its change in momentum. Thus,
4 D The impulse delivered to the ball is equal to its change in momentum. The momentum of the ball was mv before hitting the wall and m(–v) after. Therefore, the change in momentum is m(–v) – mv = –2mv, so the magnitude of the momentum change (and the impulse) is 2mv.
5 B By definition of perfectly inelastic, the objects move off together with one common velocity, v′, after the collision. By conservation of linear momentum,
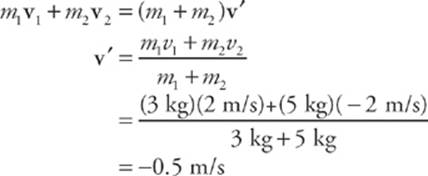
6 D First, apply conservation of linear momentum to calculate the speed of the combined object after the (perfectly inelastic) collision.
Therefore, the ratio of the kinetic energy after the collision to the kinetic energy before the collision is
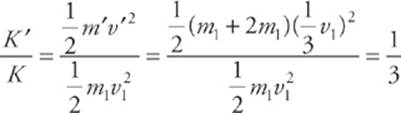
7 C Total linear momentum is conserved in a collision during which the net external force is zero. If kinetic energy is lost, then by definition, the collision is not elastic.
8 D The linear momentum of the bullet must have the same magnitude as the linear momentum of the block in order for their combined momentum after impact to be zero. The block has momentum MV to the left, so the bullet must have momentum MV to the right. Since the bullet’s massis m, its speed must be v = 
.
9 C In a perfectly inelastic collision, kinetic energy is never conserved; some of the initial kinetic energy is always lost to heat and some is converted to potential energy in the deformed shapes of the objects as they lock together.
CHAPTER 6 REVIEW QUESTIONS
1 C By combining the equation for centripetal acceleration, ac = v2/r, with v = rω, we find
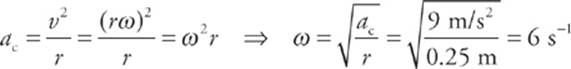
2 D The torque is τ = rF = (0.20 m)(20 N) = 4 N • m.
3 D
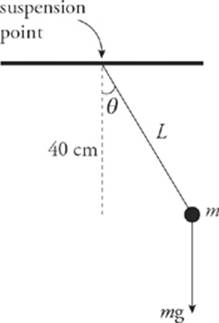
From the diagram, sinθ = 40 cm/L, so Lsinθ = 40 cm. That is, the question gave the lever arm already. (The given 60° angle was irrelevant.) Thus, from τ = Fℓ, the torque is (0.40 m)(0.50 kg)(10 m/s2) = 2.0 N • m.
4 B The stick will remain at rest in the horizontal position if the torques about the suspension point are balanced.
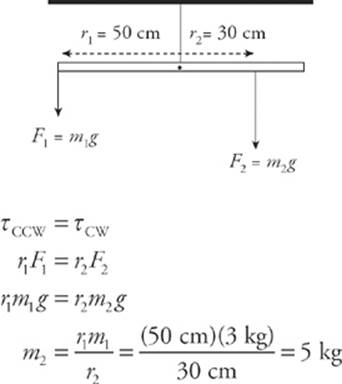
Note that the center of mass formula could also be used to find m2, though it would require algebra. Typically, the center of mass forma is useful for determining where the balance point is. If the balance point is known, then torque is usually easier.
5 E Neither the velocity nor the acceleration is constant because the direction of each of these vectors is always changing as the object moves along its circular path. And the net force on the object is not zero because a centripetal force must be acting to provide the necessary centripetal acceleration to maintain the object’s circular motion.
6 B First replace each rod by concentrating its mass at its center of mass position.
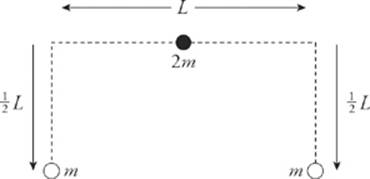
The center of mass of the two m’s is at their midpoint, at a distance of L below the center of mass of the rod of mass 2m.
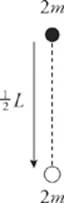
Now, applying the equation for locating the center of mass (letting y = 0 denote the position of the center of mass of the top horizontal rod), we find
7 B The gravitational pull by the earth provides the centripetal force on the satellite, so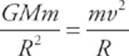 
. This gives 
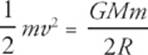, so the kinetic energy K of the satellite is inversely proportional to R. Therefore, if R increases by a factor of 2, then K decreases by a factor of 2.
8 E The gravitational pull by Jupiter provides the centripetal force on its moon.
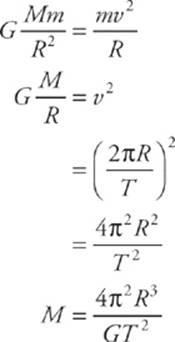
9 B Kepler’s Third Law says that T2 ∝ R3 for a planet with a circular orbit of radius R. Since T ∝ 
, if R increases by a factor of 9, then T increases by a factor of 
10 A Since the centripetal force on each satellite is equal to the gravitational force it feels due to the earth, the question is equivalent to, “How does FA, the gravitational force on satellite A, compare to FB, the gravitational force on satellite B?” Because both satellites have the same mass, Newton’s law of gravitation tells us that the gravitational force is inversely proportional to r2. Since satellite B is 3 times farther from the center of the earth than satellite A, the gravitational force that satellite B feels is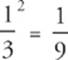 
the gravitational force felt by satellite A. (Be careful if you tried to apply the formula Fc = 
for centripetal force and concluded that the answer was B. This is wrong because even though both satellites orbit at a constant speed, they don’t orbit at the same speed, so the formula for centripetal force cannot be used directly.)
CHAPTER 7 REVIEW QUESTIONS
1 D The acceleration of a simple harmonic oscillator is not constant, since the restoring force—and, consequently, the acceleration—depends on position. Therefore, I is false. However, both II and III are fundamental, defining characteristics of simple harmonic motion.
2 C The acceleration of the block has its maximum magnitude at the points where its displacement from equilibrium has the maximum magnitude (since a =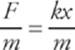 
). At the endpoints of the oscillation region, the potential energy is maximized and the kinetic energy (and hence the speed) is zero.
3 E By conservation of mechanical energy, K + US is a constant for the motion of the block. At the endpoints of the oscillation region, the block’s displacement, x, is equal to ±A. Since K = 0 here, all the energy is in the form of potential energy of the spring, kA2. Because kA2 gives the total energy at these positions, it also gives the total energy at any other position. Using the equation US(x) = kx2, we find that, at x = A
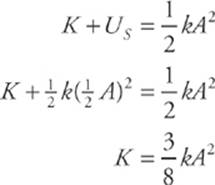
Therefore,
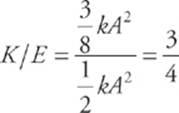
4 C As we derived in Question 2, the maximum speed of the block is given by the equation vmax =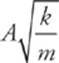 
. Therefore, vmax is inversely proportional to 
. If m is increased by a factor of 2, then vmax will decrease by a factor of 
.
5 D The period of a spring–block simple harmonic oscillator is independent of the value of g. (Recall that T =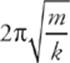 
.) Therefore, the period will remain the same.
6 D The frequency of a spring–block simple harmonic oscillator is given by the equation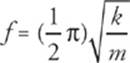 
. Squaring both sides of this equation, we get f2 = 
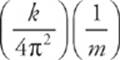Therefore, if f2 is plotted versus (1/m), then the graph will be a straight line with slope 
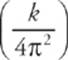. (Note: The slope of the line whose equation is y = ax is a.)
7 A The only equation that gives x = 6 when t = 0 is the one in A.
8 B The period of the spring-block simple harmonic oscillator is given by the equation T =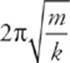 
. So, to make T as small as possible, we want m to be as small as possible and k to be as large as possible. Since m2 is the smaller mass and k1 is the larger spring constant, this combination will give the oscillator the shortest period.
9 C For small angular displacements, the period of a simple pendulum is essentially independent of amplitude.
10 B First draw a free-body diagram.
The net force toward the center of the bob’s circular path is FT – mg cosθmax. This must provide the centripetal force, 
. But since the speed of the bob at this moment is zero (v = 0), we get FT = mgcosθmax. (The acceleration is purely tangential here, equal to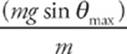 
= gsinθmax.)
CHAPTER 8 REVIEW QUESTIONS
1 D Electrostatic force obeys an inverse-square law: FE ∝ 
. Therefore, if r increases by a factor of 3, then FE decreases by a factor of 32 = 9.
2 C The strength of the electric force is given by 
, and the strength of the gravitational force is 
. Since both of these quantities have r2 in the denominator, we simply need to compare the numerical values of kq2 and Gm2. There’s no contest since
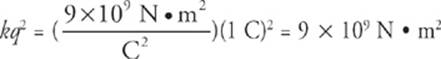
and
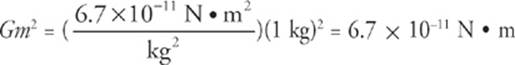
we see that kq2 > Gm2, so FE is much stronger than FG.
3 C If the net electric force on the center charge is zero, the electrical repulsion by the +2q charge must balance the electrical repulsion by the +3q charge
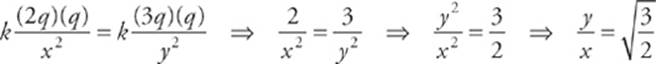
4 E Since P is equidistant from the two charges, and the magnitudes of the charges are identical, the strength of the electric field at P due to +Q is the same as the strength of the electric field at P due to –Q. The electric field vector at P due to +Q points away from +Q, and the electric field vector at P due to –Q points toward –Q. Since these vectors point in the same direction, the net electric field at P is (E to the right) + (E to the right) = (2E to the right).
5 D The acceleration of the small sphere is
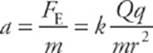
As r increases (that is, as the small sphere is pushed away), a decreases. However, since a is always positive, the small sphere’s speed, v, is always increasing.
6 B Since FE (on q) = qE, it must be true that FE (on –2q) = –2qE = –2FE.
7 D All excess electric charge on a conductor resides on the outer surface.
8 D By definition, electric field vectors point away from a positive source charge and toward a negative source charge. Furthermore, since an electron (which is negatively charged) would be repelled from a negative source charge, the resulting electric force on an electron would point away from a negative source charge, in the opposite direction from the electric field vector.
9 A The individual electric field vectors at P due to the two source charges have the same magnitude and point in opposite directions. Therefore, the net electric field at point P will be zero.
10 A The individual electric field vectors at the center of the square due to the two negative source charges cancel each other out. So we simply need to make sure that the individual electric field vector at the center of the square due to the bottom-right source charge cancels the individual electric field vector at the center of the square due to the upper-left source charge. Since the upper-left source charge is +Q, the bottom-right source charge must be +Q also.
CHAPTER 9 REVIEW QUESTIONS
1 E A counterexample for I is provided by two equal positive charges; at the point midway between the charges, the electric field is zero, but the potential is not. A counter-example for II is provided by an electric dipole (a pair of equal but opposite charges); at the point midway between the charges, the electric potential is zero, but the electric field is not. As for III, consider a single positive point charge +Q. Then at a distance r from this source charge, the electric field strength is E = 
and the potential is V = 
. Thus, V = rE, so V is not inversely proportional toE.
2 A At the center of the square, the electric fields would all cancel. The contribution from the upper-left charge would point away from it, towards the lower-right charge, but the contribution from the lower-right charge would point exactly the opposite direction and cancel it. Likewise, the contributions from the lower-left and upper-right charges would cancel.
3 E The electric potential due to any one of the charges is 
, where r = 
, since the distance from the charge to the center has that value. (To show this, draw a right triangle, the hypotenuse of which is the line from the center of the square to a charge. You’ll have a base and a height of length s/2.) That is, the potential due to one charge is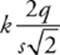 
. The potential due to four charges is just four times that potential, since electric potentials are scalars and just add together if they are all positive, so the total is 
.
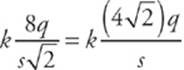4 B Use the definition ∆V = –
. If an electric field accelerates a negative charge doing positive work on it, then WE > 0. If q < 0, then – is positive. Therefore, ∆V is positive, which implies that V increases.
5 C Both electric force and electric field obey inverse square laws. The equation for electric force is F = 
, and the equation for electric field is E = 
. Thus, both of these would be one-quarter as great at twice the distance. However, electric potential is just an inverse. The equation for electric potential is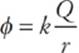 
(notice that the r is not squared). Thus, at twice the distance, it would be half as great. Thus, only Roman numeral III is true.
6 C Because E is uniform, the potential varies linearly with distance from either plate (∆V = Ed). Since points 2 and 4 are at the same distance from the plates, they lie on the same equipotential. (The equipotentials in this case are planes parallel to the capacitor plates.)
7 D As we move from point A to point B, the potential decreases by 10 V, so ∆V = –10 V. Now, since ∆U = q ∆ V, we have ∆U = (–2 C)(–10 V) = +20 J.
8 A Since Q cannot change and C is increased (because of the dielectric), ∆V = Q/C must decrease. Also, since UE =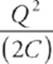 
, an increase in C with no change in Q implies a decrease in UE.
9 B By definition, WE = –q∆ V, which gives
WE = ‒q(VA ‒ VB) = ‒(‒0.05 C)(200 V ‒ 100 V) = 5 J
Notice that neither the length of the segment AB nor that of the curved path from A to B is relevant.
CHAPTER 10 REVIEW QUESTIONS
1 A Let ρS denote the resistivity of silver and let AS denote the cross-sectional area of the silver wire. Then
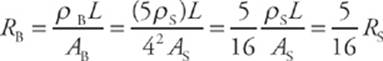
2 D The equation I = 
implies that increasing V by a factor of 2 will cause I to increase by a factor of 2.
3 C Use the equation P = 
.
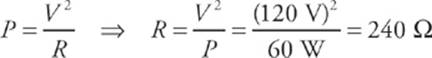
4 B The current through the circuit is
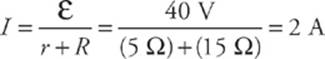
Therefore, the voltage drop across R is V = IR = (2 A)(15 Ω) = 30 V.
5 E The 12 Ω and 4 Ω resistors are in parallel and are equivalent to a single 3 Ω resistor, because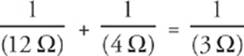 
. This 3 Ω resistor is in series with the top 3 Ω resistor, giving an equivalent resistance in the top branch of 3 Ω + 3 Ω = 6 Ω. Finally, this 6 Ω resistor is in parallel with the bottom 3 Ω resistor, giving an overall equivalent resistance of 2 Ω, because 
.
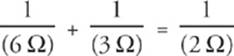6 D If each of the identical bulbs has resistance R, then the current through each bulb is ε /R. This is unchanged if the middle branch is taken out of the parallel circuit. (What will change is the total amount of current provided by the battery.)
7 D The equation P = I2R gives
P = (0.5 A)2(100 Ω) = 25 W = 25 J/s
Therefore, in 20 s, the energy dissipated as heat is
E = Pt = (25 J/s)(20 s) = 500 J
8 B Resistors in series always share the same current, so we can eliminate D and E. Now, using Ohm’s law, V = IR, we see that if I is constant, then V is proportional to R. Since RA = 4RB, we know that VA = 4VB.
CHAPTER 11 REVIEW QUESTIONS
1 D I is false: The magnetic field lines due to a current-carrying wire encircle the wire in closed loops. II is also false: Since the magnetic force is always perpendicular to the charged particle’s velocity vector, it can do work on the charged particle; therefore, it cannot change the particle’s kinetic energy. III, however, is true: If the charged particle’s velocity is parallel (or antiparallel) to the magnetic field lines, then the particle will feel no magnetic force.
2 C The magnitude of the magnetic force is FB = qvB, so the acceleration of the particle has magnitude
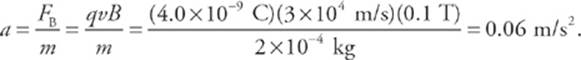
3 D By the right-hand rule, the direction of FB is out of the plane of the page (since the particle carries a negative charge).
4 E Since FB is always perpendicular to v, v cannot be upward or downward in the plane of the page; this eliminates B and C. The velocity vector also cannot be to the right, as it is in A, since then v would be antiparallel to B, and FB would be zero. Using the right-hand rule, v must be into the plane of the page.
5 A The magnetic force provides the centripetal force on the charged particle. Therefore,
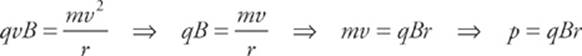
6 A The strength of the magnetic field at a distance r from a long, straight wire carrying a current I is proportional to I /r; that is, B is inversely proportional to r. So, at the distance from the wire, the magnetic field will be twice as strong.
7 E The magnetic force provides the centripetal force on the charged particle. It follows that
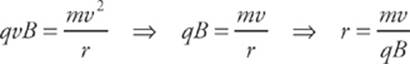
Increasing m or v, or decreasing q or B, would make r larger, not smaller. Therefore, the answer must be E.
8 D The magnetic field B cannot be in the plane of the page (because both v and FB are), so we can eliminate A, B, and C. If B pointed into the plane of the page, it’s easy to see that the right-hand rule tells us that FB would point upward in the plane of the page. Therefore, B must point out of the plane of the page.
9 E Since v is perpendicular to B, the strength of the magnetic force, FB, is just qvB, where q is the magnitude of the charge. In this case, then, we find that
FB = (0.04 C)(2 × 104 m/s)(0.5 T) = 400 N
10 C The period T is the time it takes the charge to complete one revolution: T = 
Since the magnetic force is providing the centripetal force,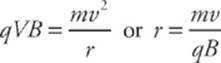 
Therefore, T = 
Since T is independent of v, it will remain unchanged.
CHAPTER 12 REVIEW QUESTIONS
1 E Since v is upward and B is out of the page, the direction of FB on the free electrons will be to the left, leaving an excess of positive charge at the right. Therefore, the potential at point b will be higher than at point a, by ε = vBL (motional emf).
2 C If the plane of a loop enclosing an area A is perpendicular to a uniform magnetic field of strength B, then the magnetic flux through the loop, ФB, is simply equal to the product BA. Since both these loops have the same area, the magnetic fluxes through them will be the same, regardless of their shape.
3 C To the right of the long straight wire, the magnetic field points into the plane of the page, and it is stronger at x1 than at x2. This means that the “into-the-page magnetic flux” through the loop increases as the loop is moved from x1 to x2. Since the flux is into the page and increasing, Lenz’s law says that the current induced in the loop will be counterclockwise to produce its own out-of-the-page magnetic flux.
4 E Since the current in the straight wire is steady, there is no change in the magnetic field, no change in magnetic flux, and, therefore, no induced emf or current.
5 C By definition, magnetic field lines emerge from the north pole and enter at the south pole. Therefore, as the north pole is moved upward through the loop, the upward magnetic flux increases. To oppose an increasing upward flux, the direction of the induced current will be clockwise (as seen from above) to generate some downward magnetic flux. Now, as the south pole moves away from the center of the loop, there is a decreasing upward magnetic flux, so the direction of the induced current will be counterclockwise.
CHAPTER 13 REVIEW QUESTIONS
1 D From the equation λf = v, we find that
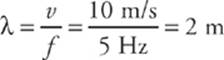
2 C The speed of a transverse traveling wave on a stretched rope is given by the equation v = 
. Therefore
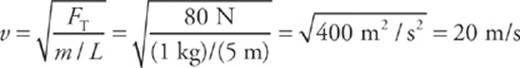
3 D The time interval from a point moving from its maximum displacement above y = 0 (equilibrium) to its maximum displacement below equilibrium is equal to one-half the period of the wave. In this case
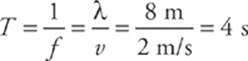
so the desired time is (4 s) = 2 s.
4 E From the equations λf = v and f = I/T, we get λ = vT = 2(cm/s)(2 s) = 4 cm.
5 E The distance between successive nodes is always equal to λ. If a standing wave on a string fixed at both ends has a total of 4 nodes, the string must have a length L equal to 3(λ). If L = 6 m, then λ must equal 4 m.
6 B We found in the previous question that λ = 4 m. Since v = 40 m/s, the frequency of this standing wave must be
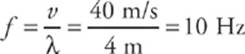
7 A In general, sound travels faster through solids than through gases. Therefore, when the wave enters the air from the metal rod, its speed will decrease. The frequency, however, will not change. Since v = λf must always be satisfied, a decrease in v implies a decrease in λ.
8 A The distance from S2 to P is 5 m (it’s the hypotenuse of a 3-4-5 triangle), and the distance from S1 to P is 4 m. The difference between the path lengths to point P is 1 m, which is half the wavelength. Therefore, the sound waves are always exactly out of phase when they reach point P from the two speakers, causing destructive interference there. By contrast, since point Q is equidistant from the two speakers, the sound waves will always arrive in phase at Q, interfering constructively. Since there’s destructive interference at P and constructive interference at Q, the amplitude at P will be less than at Q.
9 E The intensity (power per unit area) is proportional to 1/r2, where r is the distance between the source and the detector. If r increases by a factor of 10, the intensity decreases by a factor of 100. Because the decibel scale is logarithmic, if the intensity decreases by a factor of 100 = 102, the decibel level decreases by 10 log (102) = 20 dB.
10 B An air column (such as an organ pipe) with one closed end resonates at frequencies given by the equation fn = 
for odd integers n. The fundamental frequency corresponds, by definition, to n = 1. Therefore
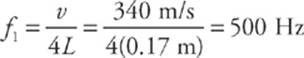
11 B The speed of the chirp is
v = λf = (8.75 × 104−3 m)(40 × 103 Hz) = 350 m/s
If the distance from the bat to the tree is d, then the wave travels a total distance of d + d = 2d (round-trip distance). If T is the time for this round-trip, then
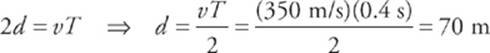
12 A Since the car is traveling away from the stationary detector, the observed frequency will be lower than the source frequency. This eliminates B and C. Using the Doppler effect equation, we find that
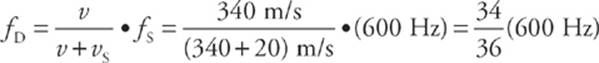
CHAPTER 14 REVIEW QUESTIONS
1 B From the equation λf = c, we find that
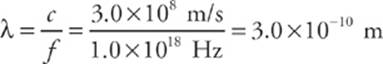
2 D Since the fringe is bright, the waves must interfere constructively. This implies that the difference in path lengths must be a whole number times the wavelength, eliminating B, C, and E. The central maximum is equidistant from the two slits, so ∆ℓ = 0 there. At the first bright fringe above the central maximum, we have ∆ℓ = λ.
3 C First, eliminate A and B: The index of refraction is never smaller than 1. Refer to the following diagram:
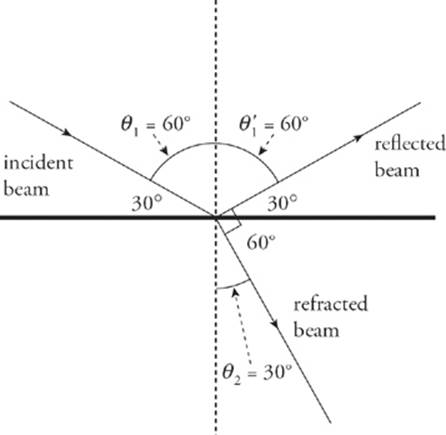
Since the reflected and refracted beams are perpendicular to each other, we have θ2 = 30°. Snell’s law then becomes
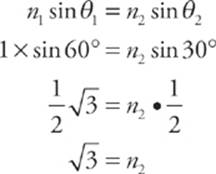
4 A The frequency is unchanged, but because the speed of light in diamond is less than in air, the wavelength of the light in diamond is shorter than its wavelength in air.
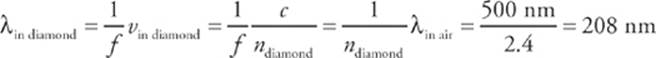
5 A If the speed of light is less in medium 2 than in medium 1, then medium 2 must have the higher index of refraction; that is, n2 > n1. Snell’s law then implies that θ2 < θ1: The beam will refract toward the normal upon transmission into medium 2.
6 A The critical angle for total internal reflection is computed as follows:
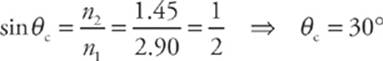
Total internal reflection can happen only if the incident beam originates in the medium with the higher index of refraction and strikes the interface of the other medium at an angle of incidence greater than the critical angle.
7 D If so = 60 cm and f = 40 cm, the mirror equation tells us that
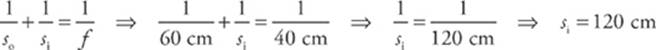
and, since si is positive, the image is real.
8 D Because the image is virtual, we must write the image distance, si, as a negative quantity: si = –20 cm. Now, with so = 60 cm, the mirror equation gives
The focal length is half the radius of curvature, so
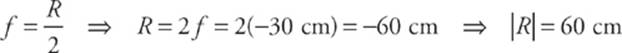
9 C Since the image is projected onto a screen, it must be real, and therefore inverted. The magnification must be negative, so
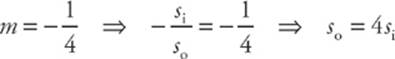
Because si = 60 cm, the object distance, so, must be 240 cm. Therefore
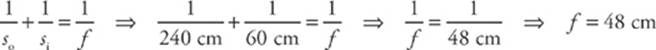
10 B A bi-concave lens is a diverging lens. Diverging lenses (like convex mirrors) have negative focal lengths and therefore cannot form real images. (Notice that D is false; diverging lenses and convex mirrors always form diminished, virtual images, as you can verify using the mirror and magnification equations.)
CHAPTER 15 REVIEW QUESTIONS
1 C Use the equation Q = mc ∆T.
Q = (0.04 kg)(0.50 kJ/kg • °C)(50°C − 20°C)=0.6 kJ = 600 J
2 D Phase changes obey the equation Q = mL, where m is the mass of the sample and L is the latent heat of transformation. In this case, we find that
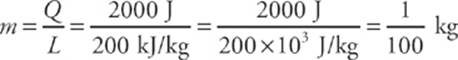
3 A First, let’s figure out how much heat is required to bring the water to its boiling point.
Q = mc∆T = (0.1 kg)(4.186 kJ/kg • °C)(100°C − 20°C) = 33 kJ
Once the water reaches 100°C, any additional heat will be absorbed and begin the transformation to steam. To completely vaporize the sample requires
Q = mL = (0.1 kg)(2260 kJ/kg) = 226 kJ
Since the 20°C water absorbed only 100 kJ of heat, enough heat was provided to bring the water to boiling, but not enough to completely vaporize it (at which point, the absorption of more heat would begin to increase the temperature of the steam). Thus, the water will reach and remain at 100°C.
4 D The equation for volume expansion is ∆V = βVi∆T, so
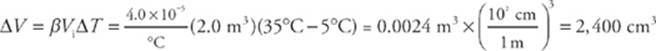
5 B Because the gas is confined, n remains constant, and because we’re told the volume is fixed, V remains constant as well. Since R is a universal constant, the ideal gas law, PV = nRT, tells us that P and T are proportional. Therefore, if T increases by a factor of 2, then so does P.
6 E Neither A nor B can be correct. Using PV = nRT, both containers have the same V, n is the same, P is the same, and R is a universal constant. Therefore, T must be the same for both samples. C is also wrong, since R is a universal constant. The kinetic theory of gases predicts that the rms speed of the gas molecules in a sample of molar mass M and temperature T is
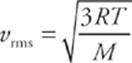
Hydrogen has a smaller molar mass than does helium, so vrms for hydrogen must be greater than vrms for helium (because both samples are at the same T).
7 A By convention, work done on the gas sample is designated as negative, so in the first law of thermodynamics, ∆U = Q – W, we must write W = –320 J. Therefore, Q = ∆U + W = 560 J + (–320 J) = +240 J. Positive Q denotes heat in.
8 C No work is done during the step from state b to state c because the volume doesn’t change. Therefore, the work done from a to c is equal to the work done from a to b. Since the pressure remains constant (this step is isobaric), we find that W = P∆V = (3.0 × 105 Pa)[(25 – 10) × 10–3m3] = 4,500 J.
9 B Since the engine takes in 400 J of energy and produces only 400 J – 300 J = 100 J of useful work, its efficiency is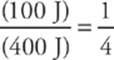 
.
10 D A is the first law of thermodynamics. C and E are true, but they are not equivalent to the second law of thermodynamics. B is false, but if it read, “The efficiency of a heat engine can never be equal to 100 percent,” then it would be equivalent to the Second Law. D is one of the several equivalent forms of the second law of thermodynamics.
CHAPTER 16 REVIEW QUESTIONS
1 B Combining the equation E = hf with f = c/ λ gives us
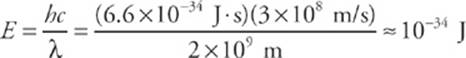
2 D The energy of the incident photons is
E = hf = (4.14 × 10–15 eV · s)(7.2 × 1015 Hz) = 30 eV
Since E > ø, photoelectrons will be produced, with maximum kinetic energy
Kmax = E – ø = 30 eV – 6 eV = 24 eV
3 A If the atom’s ionization energy is 25 eV, then the electron’s ground-state energy must be –25 eV. Making a transition from the –16 eV energy level to the ground state will cause the emission of a photon of energy.
∆E = (–16 eV) – (–25eV) = 9 eV
4 E The gap between the ground-state and the first excited state is
–10 eV – (–40 eV) = 30 eV
Therefore, the electron must absorb the energy of a 30 eV photon (at least) to move even to the first excited state. Since the incident photons have only 15 eV of energy, the electron will be unaffected.
5 C The de Broglie wavelength of a particle whose momentum is p is λ= h/p. For this proton, we find that
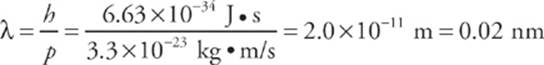
6 A In β– decay, a neutron is transformed into a proton and an electron. Therefore, the total nucleon number (mass number) doesn’t change, but the number of protons (the atomic number) increases by one.
7 A Since the mass number decreased by 4 and the atomic number decreased by 2, this is an alpha decay.
8 B After 3 half-lives, the activity will drop to (1/2)3 = 1/8 its initial value, and after 4 half-lives, it will drop to (1/2)4 = 1/16 its initial value. Since 1/10 is between 1/8 and 1/16, the time interval in this case is between 3 and 4 half-lives, that is, between 3(2.5 h) = 7.5 h and 4(2.5 h) = 10 h. Only B is in this range.
9 B In order to balance the mass number (the superscripts), we must have 2 + 63 = 64 + A, so A = 1. In order to balance the charge (the subscripts), we need 1 + 29 = 30 + Z, so Z = 0. A particle with a mass number of 1 and no charge is a neutron, 
.
10 E To balance the mass number (the superscripts), we must have 196 + 1 = 197 + A, so A = 0. To balance the charge (the subscripts), we need 78 + 0 = 78 + Z, so Z = 0. The only particle listed that has zero mass number and zero charge is a gamma-ray photon, 
.
11 C Radar waves are electromagnetic waves, and the speed of all electromagnetic waves through empty space is measured by all observers to always be c (Postulate 2 of the theory of special relativity).
12 B Special relativity dictates that length contracts for objects moving at relativistic speeds, so the length should be smaller. That’s C. (Bear in mind that the speed is attainable because the square root of three is less than 2, so the speed is less than the speed of light.) Mathematically, you could calculate the length as follows. If v = (
)c, then the relativistic factor is
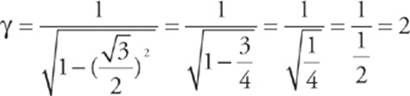
So, as measured by the inhabitants of the planet, the length of the cruiser as it passes by will be
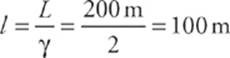
13 C Special relativity says that time dilates for objects moving at relativistic speeds, so the time should be greater (and never change). You could compute the exact value of the time as follows. If v = 
c, then the relativistic factor is
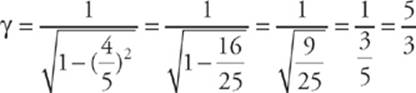
So, as measured by the team on the earth, the time interval between maintenance checks of the computer will be
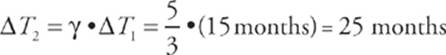
14 D Because v is close to c, the particle is relativistic, so it would be incorrect to use the formula KE = mv2. Instead, we must use the formula KE = (γ – 1)mc2. Since v = 
c, the relativistic factor is
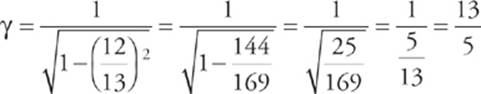
So, the kinetic energy of this particle is
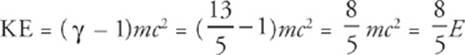
15 A Redshift occurs when light sources move away from the observer. If all the galaxies in the universe are moving away from us, that’s evidence that the universe is expanding. The Uncertainty Principle is a quantum mechanical phenomenon having to do with subatomic particles, not galaxies. The evidence that black holes exist is their gravitational effects on visible objects near them, not redshift. Dark matter has to do with anomalous rotation curves in galaxies, not redshift (though redshift—specifically, increasing redshift—is evidence for dark energy). Superconductivity has to do with conducting electricity, not galaxies.
16 D Eliminate A because Newton’s Law of Universal Gravitation is reason to believe that Newton worked on gravitation. Eliminate B because Einstein may be best known for relativity, so he did work on relativity. Eliminate C because the unit of capacitance is named after Faraday, so Faraday must have worked on electricity and magnetism. For D, though, Coulomb’s Law and the unit of electric charge are both named after Coulomb, which suggests that he significantly predated quantum mechanics and worked on the fundamentals of classical electrostatics; in fact, he was most active in the late 1700s, well before the quantum mechanics of the 1920s. Eliminate E because the Bohr model of an atom is definitely a product of Bohr’s work on atomic structure.
17 B Making simultaneous measurements of position and momentum is limited by the Uncertainty Principle, a quantum mechanical law.