SAT Physics Subject Test

Chapter 4 Work, Energy, and Power

GRAVITATIONAL POTENTIAL ENERGY

In the previous discussion, we took the surface of the earth to be our U = 0 reference level and assumed that the height, h, was small compared with the earth”s radius. In that case, the variation in g was negligible, so g was thought of as a constant.

Work and Gravity

By definition,
U_grav = –W_{by grav}

But now we”ll take variations in g into account and develop a general equation for gravitational potential energy, one that isn”t restricted to small altitude changes.

Consider an object of mass m at a distance r₁ from the center of the earth (or any spherical body) moving by some means to a position r₂.

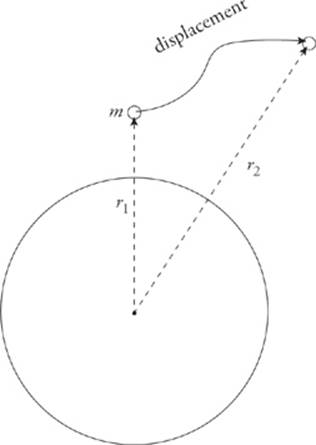
How much work did the gravitational force perform during this displacement? The answer is given by the equation.

W_{by grav} = GMm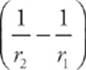

Therefore, since ∆U_grav = –W_{by grav}, we get

U₂ –U₁ = –GMm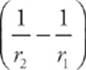

Let”s choose our U = 0 reference at infinity. That is, we decide to allow U₂ → 0 as r₂ → ∞. Then this equation becomes

U = −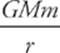

Notice that according to this equation (and our choice of U = 0 when r = ∞), the gravitational potential energy is always negative. This just means that energy has to be added to bring an object (mass m) bound to the gravitational field of M to a point very far from M, at which U = 0.

14. A satellite of mass m is in a circular orbit of radius R around the earth (radius r_E, mass M). What is its total mechanical energy (where U_grav is considered zero as R approaches infinity)?

Here”s How to Crack It

The mechanical energy, E, is the sum of the kinetic energy, K, and potential energy, U. You can calculate the kinetic energy, since you know that the centripetal force on the satellite is provided by the gravitational attraction of the earth.

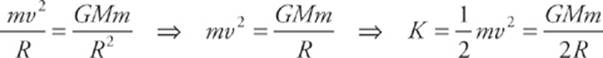
Therefore
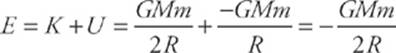