SAT Physics Subject Test

Chapter 6 Curved and Rotational Motion

So far we”ve studied only translational motion—objects sliding, falling, or rising—but you”ll also need to know about spinning objects for the SAT Physics Subject Test. We will now look at rotation.

UNIFORM CIRCULAR MOTION

In Chapter 2, we considered two types of motion: straight-line motion and parabolic motion. We will now look at motion that follows a circular path, such as a rock on the end of a string, a horse on a merry-go-round, and (to a good approximation) the moon around Earth and Earth around the sun.

Let”s simplify matters and consider the object”s speed around its path to be constant. This is called uniform circular motion. You should remember that in these situations, although the speed may be constant, the velocity is not because the direction of the velocity is always changing. Since the velocity is changing, there must be acceleration. This acceleration doesn”t change the speed of the object; it changes only the direction of the velocity to keep the object on its circular path. Also, to produce an acceleration, there must be a force; otherwise, the object would move off in a straight line (Newton”s first law).

The figure on the left below shows an object moving along a circular trajectory, along with its velocity vectors at two nearby points. The vector v₁ is the object”s velocity at time t = t₁, and v₂ is the object”s velocity vector a short time later (at time t = t₂). The velocity vector is always tangential to the object”s path (whatever the shape of the trajectory). Notice that since we are assuming constant speed, the lengths of v₁ and v₂ (their magnitudes) are the same.

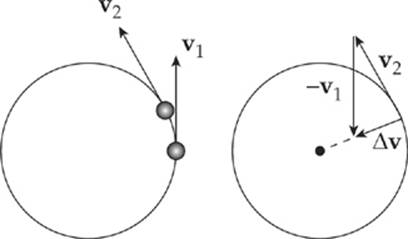
Since ∆v = v₂ – v₁ points toward the center of the circle (see the figure on the right), so does the acceleration, since a = ∆v/∆t. And because the acceleration vector points toward the center of the circle, it”s called centripetal acceleration, or a^c. The centripetal acceleration is what turns the velocity vector to keep the object traveling in a circle.

The magnitude of the centripetal acceleration depends on the object”s speed, v, and the radius, r, of the circular path according to the following equation:

a_c =

1. An object of mass 5 kg moves at a constant speed of 6 m/s in a circular path of radius 2 m. Find the magnitude of the object”s acceleration and the net force responsible for its motion.

Here”s How to Crack It

By definition, an object moving at constant speed in a circular path is undergoing uniform circular motion. Therefore, it experiences a centripetal acceleration of magnitude v²/r, which is always directed toward the center of the circle.

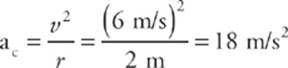
Newton”s second law, coupled with the equation for centripetal acceleration, gives:

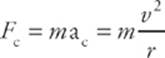
What is the
Centripetal Force?

The centripetal force is not
a new force that makes
things move in circles.
Rather, real forces (e.g.
gravity, friction, tension,
the normal) provide
the centripetal force
necessary to maintain
circular motion.

This equation gives the magnitude of the force. As for its direction, remember that because F = ma, the directions of F and a are always the same. Since centripetal acceleration points toward the center of the circular path, so does the force that produces it. Therefore, it”s called centripetal force. The centripetal force acting on this object has a magnitude of F_c = ma_c = (5 kg)(18 m/s²) = 90 N.

2. A 10 kg mass is attached to a string that has a breaking strength of 1,500 N. If the mass is whirled in a horizontal circle of radius 90 cm, what is the maximum speed it can have? (Neglect the effects of gravity.)

Work and
Circular Motion

All centripetal forces do
no work, since the force is
directed toward the center
and the motion is tangent
to the circle.

Here”s How to Crack It

The first thing to do in problems like this is to identify what force(s) provide the centripetal force. In this example, the tension in the string provides the centripetal force:

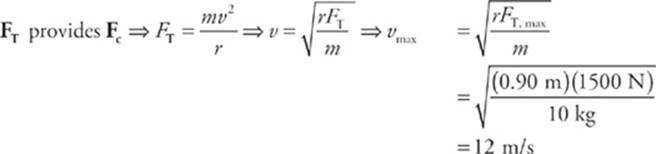
Centripetal vs.
Centrifugal

Centripetal force is
the force necessary to
maintain circular motion,
directed toward the
center. The so-called
“centrifugal force” is
what an object feels as
it moves in a circle (an
outward “force”). This is
not actually a force, but
the effect of the object”s
inertia (its resistance to
acceleration).

3. A roller-coaster car enters the circular-loop part of the ride. At the very top of the circle (where the people in the car are upside down), the speed of the car is v and the acceleration points straight down. If the radius of the loop is r and the total mass of the car (plus passengers) is m, find the magnitude of the normal force exerted by the track on the car at this point.

Here”s How to Crack It

There are two forces acting on the car at its highest point: the normal force exerted by the track and the gravitational force, both of which point downward.

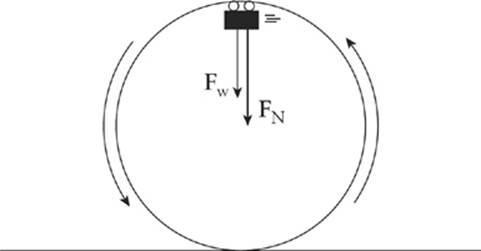
The combination of these two forces, F_N + F_w, provides the centripetal force, so

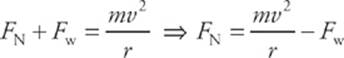
4. In the previous example, if the net force on the car at its highest point is straight down, why doesn”t the car fall straight down?

Here”s How to Crack It

Remember that force tells an object how to accelerate. If the car had zero velocity at this point, then it would fall straight down, but the car has a nonzero velocity (to the left) at this point. The fact that the acceleration is downward means that, at the next moment v will point down and to the left at a slight angle, ensuring that the car remains on a circular path, in contact with the track. This contact force is the normal force. You can think of the normal force as a measure of the strength of contact between two surfaces. If it is a high value, they are pressing very hard against one another. If it is a low value, they are not pressing very hard against one another. It is easy to see, then, that if the normal force is zero, there is no contact between the cart and the surface. So long as the normal force is not zero, the cart is still in contact with the surface.

5. In the previous examples, what is the minimum speed necessary to keep the roller coaster on the track at all times?

Here”s How to Crack It

The position where the roller coaster is most in danger of leaving the track is at the top.

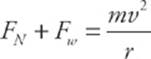
The slower the object moves, the smaller F_N gets (F_W is a constant). Therefore, the minimum speed occurs when F_N =0. (For a moment, the rollercoaster is touching the track but not pressed against it; it”s almost losing contact.)

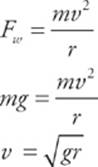
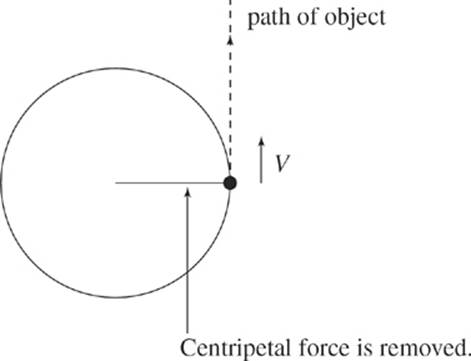
If the centripetal force acting on an object were suddenly removed, Newton”s first law says that the object would move in a straight line with constant velocity (until another force acts on it). This means that the object would move in the direction it was moving when the force was removed (i.e., tangent to the circle).