SAT Physics Subject Test

Chapter 6 Curved and Rotational Motion

ANGULAR MOMENTUM

So far we”ve developed rotational analogs for displacement, velocity, acceleration, and force. We will finish by developing a rotational analog for linear momentum; it”s called angular momentum.

Consider a small point mass m at distance r from the axis of rotation, moving with velocity v and acted upon by a tangential force F.

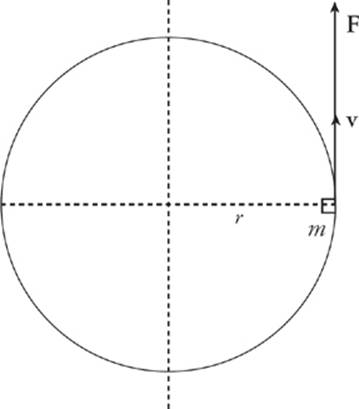
Then, by Newton”s second law

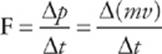
If we multiply both sides of this equation by r and notice that rF = τ, we get

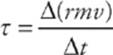
Therefore, to form the analog of the law F = ∆p/∆t (force equals the rate-of-change of linear momentum), we say that torque equals the rate-of-change of angular momentum, and the angular momentum (denoted by L) of the point mass m is defined by the equation

L = rmv

If the point mass m does not move in a circular path, we can still define its angular momentum relative to any reference point.

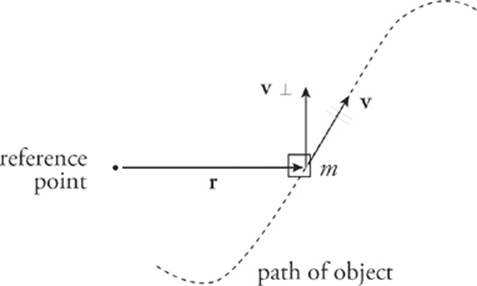
If r is the vector from the reference point to the mass, then the angular momentum is

L = rmv_⊥

where v_⊥ is the component of the velocity that”s perpendicular to r.

For a rotating object, the angular momentum equals the sum of the angular momentum of each individual particle. This can be written as L=Iω, where I is the object”s moment of inertia and ω is the angular velocity (to be discussed later). I is basically a measure of how difficult it is to start an object rotating (analogous to mass in the translational world). I increases with mass and average radius from the axis of rotation.