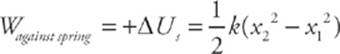SAT Physics Subject Test

Chapter 7 Oscillations

In this chapter, we”ll concentrate on a kind of periodic motion that”s straightforward and that, fortunately, actually describes many real-life systems. This type of motion is called simple harmonic motion. Many of the examples of this that you”ll see on the SAT Physics Subject Test involve a block that”s oscillating on the end of a spring. Here we”ll learn about this simple system, and we can apply our knowledge to many other oscillating systems.

SIMPLE HARMONIC MOTION (SHM): THE SPRING–BLOCK OSCILLATOR

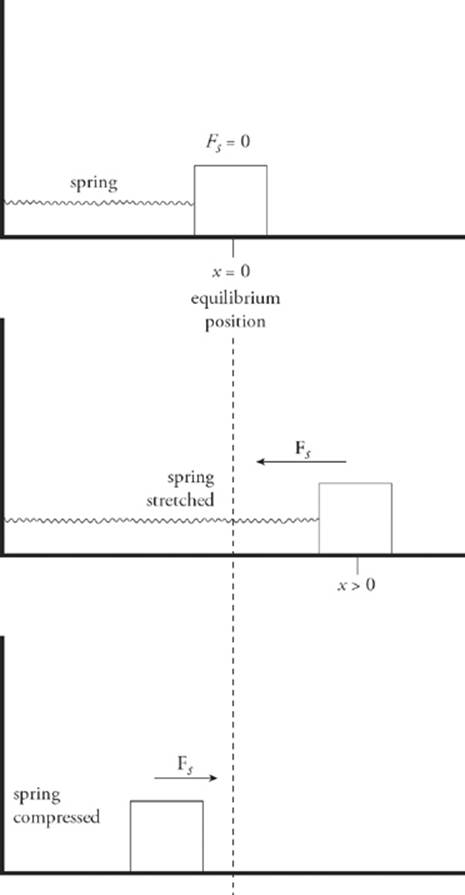
When a spring is compressed or stretched from its natural length, a force is created. If the spring is displaced by x from its natural length, the force it exerts in response is given by the equation

F_S = –kx

This is known as Hooke”s law. The proportionality constant, k, is a positive number called the spring (or force) constant that indicates how stiff the spring is. The stiffer the spring, the greater the value of k. The minus sign in Hooke”s law tells us that F_S and x always point in opposite directions. For example, referring to the figure below, when the spring is stretched (x is to the right), it then pulls back (F is to the left); when the spring is compressed (x is to the left), it then pushes outward (F is to the right). In all cases, the spring wants to return to its original length. As a result, the spring tries to restore the attached block to the equilibrium position, which is the position at which the net force on the block is zero. For this reason, we say that the spring provides a restoring force.

1. A 12 cm-long spring has a force constant (k) of 400 N/m. How much force is required to stretch the spring to a length of 14 cm ?

Here”s How to Crack It

The displacement of the spring has a magnitude of 14 – 12 = 2 cm = 0.02 m, so according to Hooke”s law, the spring exerts a force of magnitude F = kx = (400 N/m)(0.02 m) = 8 N. Therefore, we”d have to exert this much force to keep the spring in this stretched state.

Springs that obey Hooke”s law (called ideal or linear springs) provide an ideal mechanism for defining the most important kind of vibrational motion: simple harmonic motion.

Consider a spring with force constant k, attached to a vertical wall, with a block of mass m on a frictionless table attached to the other end.

Grab the block, pull it some distance from its original position, and release it. The spring will pull the block back toward equilibrium. Of course, because of its momentum, the block will pass through the equilibrium position and compress the spring. At some point, the block will stop, and the compressed spring will push the block back. In other words, the block will oscillate.

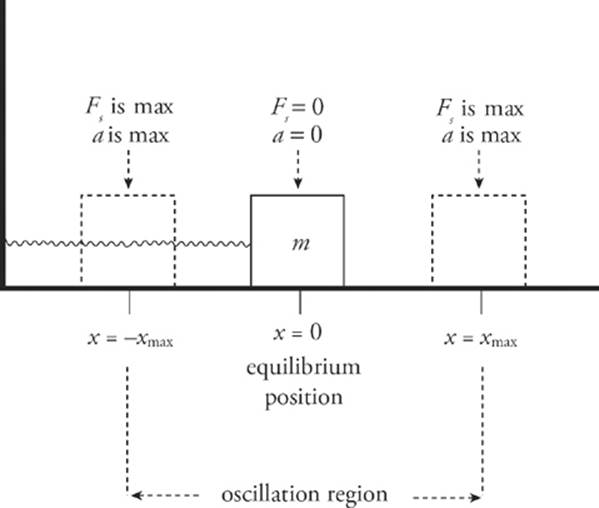
During the oscillation, the force on the block is zero when the block is at equilibrium (the point we designate as x = 0). This is because Hooke”s law says that the strength of the spring”s restoring force is given by the equation F_S = kx, so F_S = 0 at equilibrium. The acceleration of the block is also equal to zero at x = 0, since F_S = 0 at x = 0 and a = F_S/m. At the endpoints of the oscillation region, where the block”s displacement, x, is largest, the restoring force and the magnitude of the acceleration are both at their maximum.

SHM in Terms of Energy

Another way to describe an oscillating block”s motion is in terms of energy transfers. A stretched or compressed spring stores elastic potential energy, which is transformed into kinetic energy (and back again); this shuttling of energy between potential and kinetic causes the oscillations. For a spring with spring constant k, the elastic potential energy it possesses—relative to its equilibrium position—is given by the equation

U_S = kx²

Notice that the farther you stretch or compress a spring, the more work you have to do, and, as a result, the more potential energy is stored.

In terms of energy transfers, we can describe the block”s oscillations as follows: When you initially pull out the block, you increase the elastic potential energy of the system. When you release the block, this potential energy turns into kinetic energy, and the block moves. As it passes through equilibrium, U_S = 0, so all the energy is kinetic. Then, as the block continues through equilibrium, it compresses the spring and the kinetic energy is transformed back into elastic potential energy.

By conservation of mechanical energy, the sum K + U_S is a constant. Therefore, when the block reaches the endpoints of the oscillation region (that is, when x = ±x_max), U_S is maximized, so K must be minimized; in fact, K = 0 at the endpoints. As the block is passing through equilibrium, x = 0, so U_S = 0 and K is maximized.

Please note, the figure on the previous page and the figure on this page are very important. Be sure you understand them and everything in this section before you take the test!

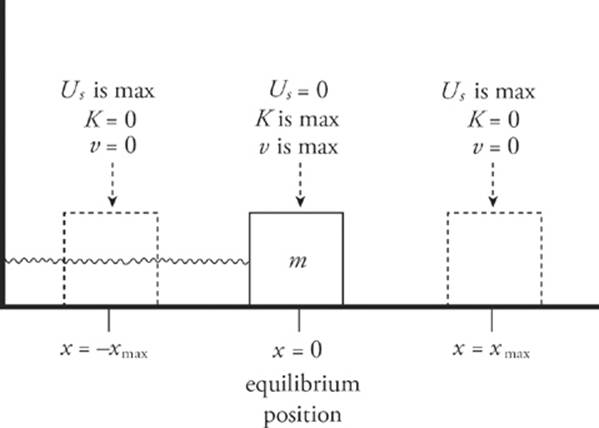
The maximum displacement from equilibrium is called the amplitude of oscillation, or A. So instead of writing x = x_max, we write x = A (and x = –x_max will be written as x = –A).

2. A block of mass m = 0.2 kg oscillates on a spring whose force constant k is 500 N/m. The amplitude of the oscillations is 4.0 cm. Calculate the maximum speed of the block.

Here”s How to Crack It

First let”s get an expression for the maximum elastic potential energy of the system, which occurs when x = x_max = A.

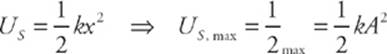
When all this energy has been transformed into kinetic energy—which, as we discussed earlier, occurs just as the block is passing through equilibrium—the block will have maximum kinetic energy and maximum speed.

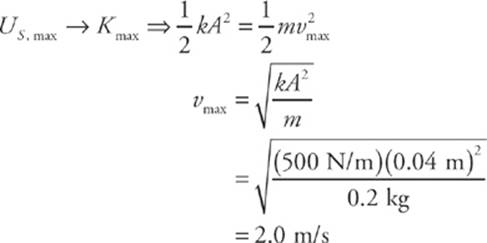
3. A block of mass m = 2.0 kg is attached to an ideal spring of force constant k = 200 N/m. The block is at rest at its equilibrium position. An impulsive force acts on the block, giving it an initial speed of 2.0 m/s. Find the amplitude of the resulting oscillations.

Here”s How to Crack It

The block will come to rest when all of its initial kinetic energy has been transformed into the spring”s potential energy. At this point, the block is at its maximum displacement from equilibrium, that is, it”s at one of its amplitude positions, and

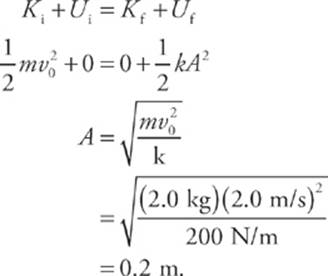
Because F_s varies as the object moves, the work done by or against the spring cannot be written as Fd cosθ. As with gravity, we must calculate work in terms of potential energy. If a block on a spring moves from x₁ to x₂, then

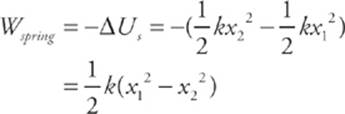
If an external force compresses or stretches the spring, then