SAT Physics Subject Test

Chapter 9 Electric Potential and Capacitance

ELECTRIC POTENTIAL

Consider a point charge q₁ at a distance r₁ from a fixed charge q₂ moving by some means to a position r₂

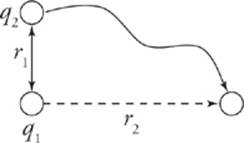
How much work did the electric force perform during this displacement? The answer is given by the equation W_E = −kq₁q₂ .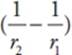

Therefore, since ΔU_E = –W_E we get U₂ – U₁ = kq₁q₂ .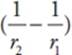

Let”s choose our U=U reference at infinity. Then this equation becomes U_E = .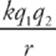

Notice that if q₁ and q₂ have the same sign, U_E is positive. This means it took positive work by an external force to bring these charges together (since they repel each other). If q₁ and q₂ have opposite signs, U_E is negative. This means the electric force does positive work to bring these changes together (since they attract).

Let”s look at another example.

Let W_E be the work done by the electric field on a charge q as it undergoes a displacement. If another charge that”s twice as strong, say 2q, were to undergo the same displacement, the electric force would be twice as great on this second charge, and the work done by the electric field would be twice as much, 2W_E. Since the work would be twice as much in the second case, the change in electrical potential energy would be twice as great as well, but the ratio of the change in potential energy to the charge would be the same: 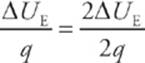. This ratio says something about thefield and the displacement, but not the charge that made the move. The change in electric potential, V, is defined as this ratio.

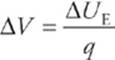
Electric potential is electrical potential energy per unit charge; the units of electric potential are joules per coulomb. One joule per coulomb is called one volt (abbreviated V); so 1 = 1 V.

Consider the electric field that”s created by a point source charge Q. The electric potential at a distance r from Q is

V =

Notice that the potential depends on the source charge making the field and the distance from it.

3. Let Q = 2 10^–9 C. What is the potential at a point P that is 2 cm from Q ?

Here”s How to Crack It

Relative to V = 0 at infinity, we have

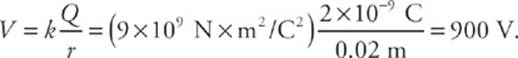
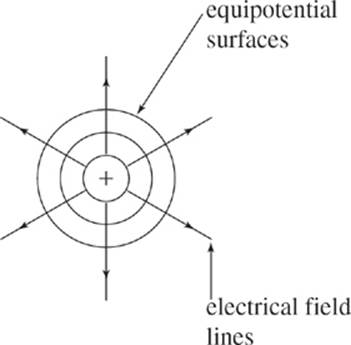
Notice that, like potential energy, potential is a scalar. In the preceding example, we didn”t have to specify the direction of the vector from the position of Q to the point P because it didn”t matter. At any point on a sphere that”s 2 cm from Q, the potential will be 900 V. These spheres aroundQ are called equipotential surfaces, and they”re surfaces of constant potential. Their cross sections in any plane are circles and are, therefore, perpendicular to the electric field lines. The equipotentials are always perpendicular to the electric field lines.

4. How much work is done by the electric field as a charge moves along an equipotential surface?

Here”s How to Crack It

If the charge always remains on a single equipotential, then the potential, V, never changes. Therefore, ΔV = 0, so Δ U_E = 0. Since W_E = –Δ U_E, the work done by the electric field is zero.

5. Two large, flat plates—one carrying a charge of +Q, the other –Q—are separated by a distance d. The electric field between the plates, E, is uniform. Determine the potential difference between the plates.

Potential vs.
Potential Energy

Remember that everything
naturally tends toward
lower potential energy.
Positive charges tend
toward lower potential
and negative charges tend
toward higher potential.

Here”s How to Crack It

Imagine a positive charge q moving from the positive plate to the negative plate.

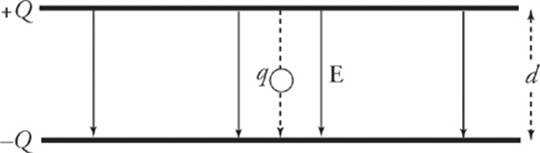
Since the work done by the electric field is

W_E,+→− = F_Ed = qEd

the potential difference between the plates is

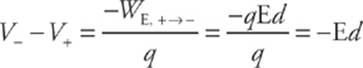
This tells us that the potential of the positive plate is greater than the potential of the negative plate, by the amount Ed.