SAT Physics Subject Test
Chapter 9 Electric Potential and Capacitance
DIELECTRICS
One method of keeping the plates of a capacitor apart, which is necessary to maintain charge separation and store potential energy, is to insert an insulator (called a dielectric) between the plates.
A dielectric always increases the capacitance of a capacitor.
Let”s see why this is true. Imagine charging a capacitor to a potential difference of Δ V with charge +Q on one plate and –Q on the other. Now disconnect the capacitor from the charging source and insert a dielectric. What happens? Although the dielectric is not a conductor, the electric field that existed between the plates causes the molecules within the dielectric material to polarize; there is more electron density on the side of the molecule near the positive plate.
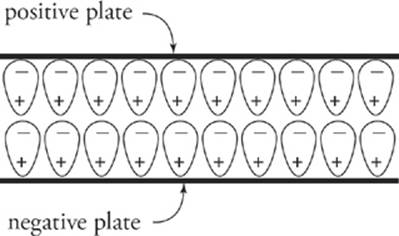
The effect of this is to form a layer of negative charge along the top surface of the dielectric and a layer of positive charge along the bottom surface; this separation of charge induces its own electric field (Ei), within the dielectric, which opposes the original electric field, E, within the capacitor.
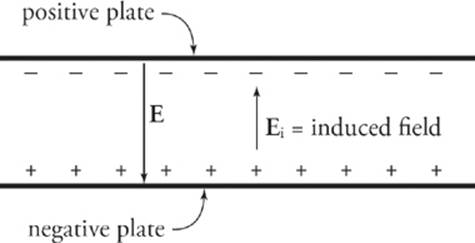
So the overall electric field has been reduced from its previous value: Etotal = E + Ei, and Etotal= E – Ei. Let”s say that the electric field has been reduced by a factor of k (the Greek letter kappa) from its original value as follows
Ewith dielectric = Ewithout dielectric –Ei = ![]()
Since ∆V = Ed for a parallel-plate capacitor, we see that ∆V must have decreased by a factor of k. But C = ![]() , so if ∆V decreases by a factor of k, then C increases by a factor of k:
, so if ∆V decreases by a factor of k, then C increases by a factor of k:
Cwith dielectric =kCwithout dielectric
The value of k, called the dielectric constant, varies from material to material, but it”s always greater than 1.
9. A parallel-plate capacitor with air between its plates has a capacitance of 2 × 10–6 F. What will be the capacitance if the capacitor is fitted with a dielectric whose dielectric constant is 3 ?
Here”s How to Crack It
The capacitance with a dielectric is equal to k times the capacitance without, where k is the dielectric constant. So
Cwith dielectic = kCwithout dielectic = (3)(2 × 10–6 F) = 6 × 10–6 F.
Remember that a capacitor with a dielectric always has a greater capacitance than the same capacitor without a dielectric.
![]()