SAT Physics Subject Test
Chapter 10 Direct Current Circuits
RESISTANCE–CAPACITANCE (RC) CIRCUITS
Capacitors are typically charged by batteries. Once the switch in the diagram on the left is closed, electrons are attracted to the positive terminal of the battery and leave the top plate of the capacitor. Electrons also accumulate on the bottom plate of the capacitor, and this continues until the voltage across the capacitor plates matches the emf of the battery. When this condition is reached, the current stops and the capacitor is fully charged.
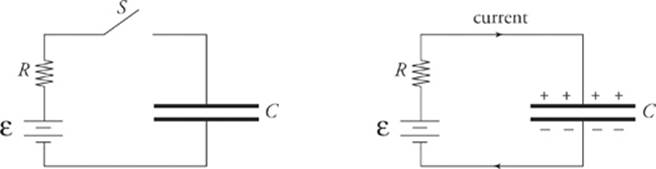
![]()
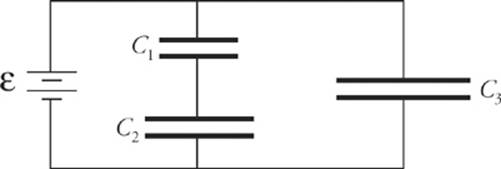
12. Find the charge stored and the voltage across each capacitor in the following circuit, given that ε = 180 V, C1 = 30 μ F, C2 = 60 μ F, and C3 = 90 μ F.
Here”s How to Crack It
Once the charging currents stop, the voltage across C3 is equal to the voltage across the battery, so V3 = 180 V. This gives us Q3 = C3V3 = (90μF)(180 V) = 16.2 mC. Since C1 and C2 are in series, they must store identical amounts of charge, and, from the diagram, the sum of their voltages must equal the voltage of the battery. So if we let Q be the charge on each of these two capacitors, then Q = C1V1 = C2V2 and V1 + V2 = 180 V. The equation C1V1 = C2V2 becomes (30μF)V1 = (60μF)V2, so V1 = 2V2. Substituting this into V1 + V2 = 180 V gives us V1 = 120 V and V2 = 60 V.The charge stored on each of these capacitors is
(30μF)(120 V) = C1V1 = C2V2 = (60μF)(60 V) = 3.6 mC
![]()
![]()
13. In the diagram below, C1 = 2 mF and C2 = 4 mF. When switch S is open, a battery (which is not shown) is connected between points a and b and charges capacitor C1 so that Vab = 12 V. The battery is then disconnected.
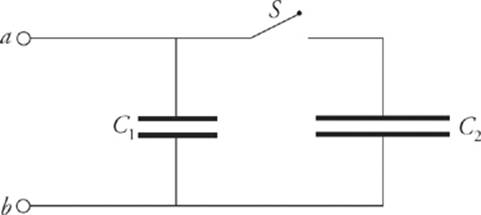
After the switch is closed, what will be the common voltage across each of the parallel capacitors (once electrostatic conditions are reestablished)?
Here”s How to Crack It
When C1 is fully charged, the charge on (each of the plates of) C1 has the magnitude Q = C1V = (2 mF)(12 V) = 24 mC. After the switch is closed, this charge will be redistributed in such a way that the resulting voltages across the two capacitors, V′, are equal. This happens because the capacitors are in parallel. So if Q′1 is the new charge magnitude on C1 and Q′2 is the new charge magnitude on C2, we have Q′1 + Q′2 = Q, so C1V′ + C2V′ = Q, which gives us
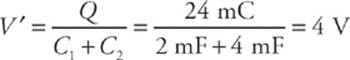
![]()