SAT Physics Subject Test
Chapter 13 Waves
THE DOPPLER EFFECT
When a source of sound waves and a detector are not in relative motion, the frequency that the source emits matches the frequency that the detector receives.
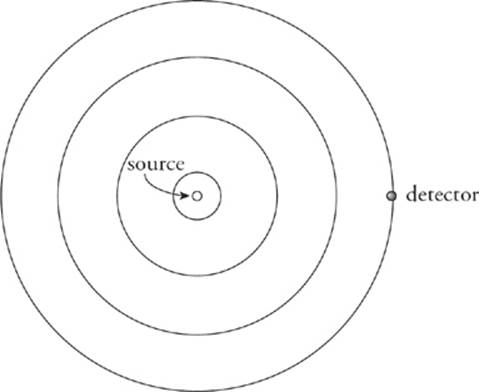
However, if there is relative motion between the source and the detector, then the waves that the detector receives are different in frequency. For example, if the detector moves toward the source, then the detector intercepts the waves at a rate higher than the one at which they were emitted; the detector hears a higher frequency than the source emitted. In the same way, if the source moves toward the detector, the wavefronts pile up, and this results in the detector receiving waves with shorter wavelengths and higher frequencies.
Note that when the detector moves and not the source, there is no change in wavelength. Instead, there is a change to the speed with which the detector receives wavefronts.
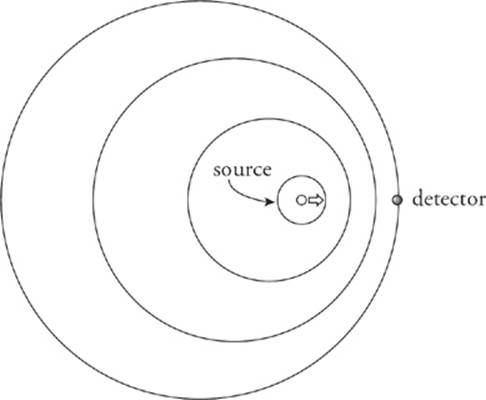
Conversely, if the detector is moving away from the source or if the source is moving away from the detector
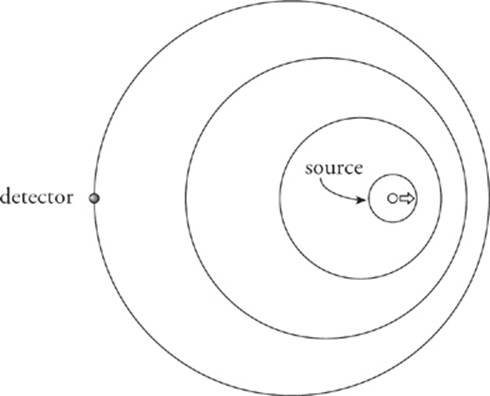
then the detected waves have a lower frequency than they had when they were emitted by the source. The shift in frequency that occurs when the source and detector are in relative motion is known as the Doppler effect. In general, relative motion toward each other results in a frequency shift upward, and relative motion away from each other results in a frequency shift downward.
Let fS be the frequency of waves that the source emits and fD the frequency that the detector hears. To determine fD from fS, use the following equation:
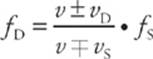
where v is the speed of sound, vD is the speed of the detector, and vS is the speed of the source. The signs in the numerator and denominator depend on the directions in which the source and detector are moving: Use the higher sign in the numerator or denominator for motion towards and the lower for motion away.
For example, consider the case of a detector moving toward a stationary source. Since the source doesn”t move, vS = 0, and there”s no decision to be made about the sign in the denominator. However, because vD is not zero (the detector is moving), we need to decide whether to use the + or the – in the numerator. Since the detector moves toward the source, we expect a frequency shift upward. Therefore, to give the higher frequency predicted by the Doppler effect, the + sign must be used.
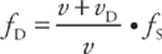
If the detector had been moving away from the source, we would have used the – sign in the numerator, to get the lower frequency.
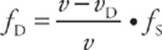
If both the source and the detector are moving, simply make each decision (+ or – in the numerator for vD and + or – in the denominator for vS) separately. For example, consider a car following a police car whose siren emits a sound of constant frequency. In this case, both the source (the police car) and the detector (the driver of the pursuing car) are moving. Because the detector is moving toward the source, we should use the + sign on vD in the numerator for an upward contribution to fD. Since the source is moving away from the detector, we should use the + sign on vS in the denominator for a downward contribution to fD. Therefore, we get
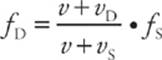
We can learn something else from this. What if the car were moving at the same speed as the police car? Then, although both are moving relative to the road, they are not moving relative to each other. If there is no relative motion between the source and the detector, then there should be no Doppler shift, since vD = vS implies that fD = fS.
![]()
Questions 19-20
A source of 4 kHz sound waves travels at ![]() the speed of sound toward a detector that”s moving at
the speed of sound toward a detector that”s moving at ![]() the speed of sound, toward the source.
the speed of sound, toward the source.
19. What is the frequency of the waves as they”re received by the detector?
Here”s How to Crack It
19. Because the detector moves toward the source, we use the + sign in the numerator of the Doppler effect formula, and since the source moves toward the detector, we use the – sign in the denominator. This gives us
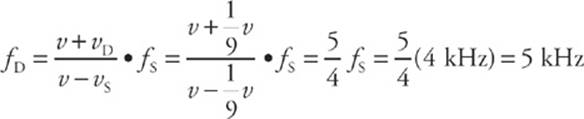
![]()
![]()
20. A train sounds its whistle as it travels at a constant speed by a train station. Describe the pitch of the train”s whistle as heard by someone standing on the station platform.
Here”s How to Crack It
Because the “pitch” of a sound is its frequency, we want to describe the frequency of the train whistle as heard by someone on the platform. As the train approaches the platform, the frequency detected will be higher than the frequency emitted by the train; then, as the train recedes from the platform, the frequency detected will be lower than the frequency emitted by the train. So, a person standing on the platform hears a higher pitch as the train approaches and a lower pitch as it travels away.
![]()