SAT Physics Subject Test
Chapter 14 Optics
INTERFERENCE AND DIFFRACTION
As we learned in the preceding chapter, waves experience interference when they meet, and whether they interfere constructively or destructively depends on their relative phase. If they meet in phase (crest meets crest), they combine constructively, but if they meet out of phase (crest meets trough), they combine destructively. The key to the interference patterns we”ll study in the next section rests on these points. In particular, if waves that have the same wavelength meet, then the difference in the distances they”ve traveled determine whether they are in phase. Assuming that the waves are coherent (which means that their phase difference remains constant over time and does not vary), if the difference in their path lengths, ∆ ℓ, is a whole number of wavelengths—0, ± λ, ±2λ, etc.—they”ll arrive in phase at the meeting point. However, if this difference is a whole number plus one-half a wavelength—±![]() λ, ±(1 +
λ, ±(1 + ![]() )λ, ±(2 +
)λ, ±(2 +![]() )λ, etc.—then they”ll arrive exactly out of phase. That is
)λ, etc.—then they”ll arrive exactly out of phase. That is
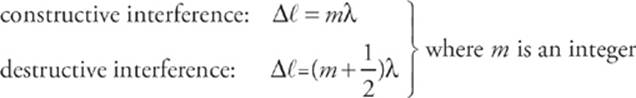
Young”s Double-Slit Interference Experiment
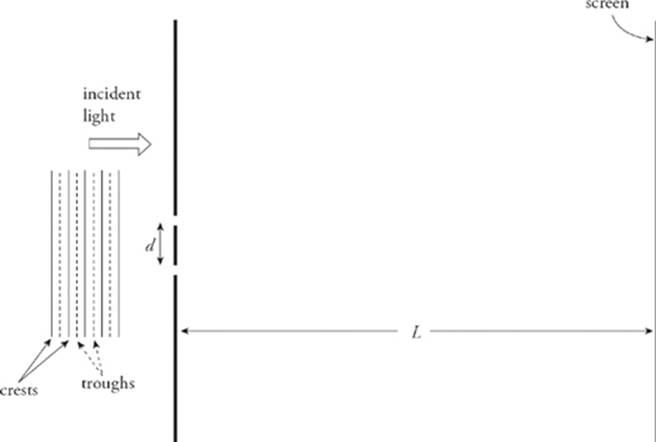
The following figure shows light incident (shining) on a barrier that contains two narrow slits (perpendicular to the plane of the page), separated by a distance d. On the right is a screen whose distance from the barrier, L, is much greater than d. The question is, what will we see on the screen? You might expect to see just two bright narrow strips of light, directly opposite the slits in the barrier, but this is not what happens.
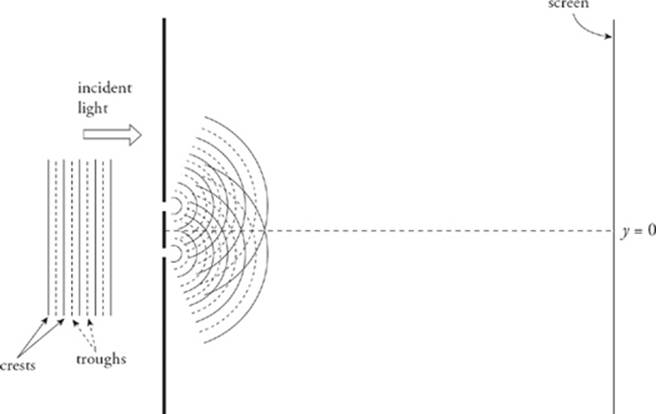
When a wave encounters a slit with a width that”s comparable with its wavelength, the wave will fan out after it passes through. This phenomenon is called diffraction. In the set-up above, the waves will diffract through the slits and spread out and interfere as they travel toward the screen.
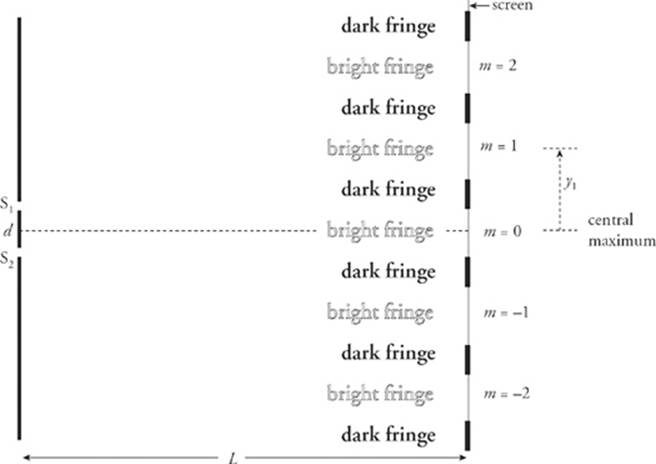
The screen shows the results of this interference: There will be bright bands (fringes) centered at those points at which the waves interfere constructively, alternating with dark fringes, where the waves interfere destructively.
To locate the positions of, say, the bright fringes on the screen, we use the equation.
ym = ![]()
Where y measures the vertical displacement along the screen from the center of the screen (y = 0, the point directly across from the midpoint of the slits). The bright fringe directly opposite the midpoint of the slits—the central maximum—will have the greatest intensity, the bright fringes with m = ±1 will have a lower intensity, those with m = ±2 will be fainter still, and so on. If more than two slits are cut in the barrier, the interference pattern becomes sharper, and the distinction between dark and bright fringes becomes more pronounced. Barriers containing thousands of tiny slits per centimeter—called diffraction gratings—are used precisely for this purpose.
![]()
Questions 3-4
For the experimental set-up we”ve been studying, assume that d = 1 mm, L = 6.0 m, and that the light used has a wavelength of 600 nm.
3. How far above the center of the screen will the first bright fringe appear?
4. What would happen to the interference pattern if the slits were moved closer together?
Here”s How to Crack It
3. The central maximum corresponds to m = 0 (y0 = 0). The first maximum above the central one is labeled y1 (since m = 1), and the first maximum below the central one is labeled y–1 (that is, m = –1). The other bright fringes on the screen are labeled accordingly.
The value of y1 is
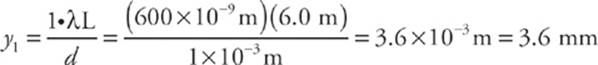
4. Since ym = mλ/d, a decrease in d would cause an increase in ym. In other words, the fringes would become larger and the interference pattern would be more spread out.
![]()
Single-Aperture Diffraction
A diffraction pattern will also form on the screen if the barrier contains only one slit. The central maximum will be very pronounced, but lower-intensity maxima will also be seen because of interference from waves arriving from different locations within the slit itself. The central maximum will become wider as the width of the slit is decreased.