SAT Physics Subject Test
Chapter 15 Thermal Physics
PHYSICAL CHANGES DUE TO HEAT TRANSFER
Calorimetry I: Heat Transfer and Temperature Change
The change in temperature that a substance experiences upon a transfer of heat depends on two things: the identity and the amount of the substance present. For example, we could transfer 200 J of heat to a gold nugget and a piece of wood of equal mass and, even though they were infused with the same amount of thermal energy, the temperature of the gold would rise much more than the temperature of the wood. Also, if this heat were transferred to two nuggets of gold of unequal mass, the temperature of the smaller nugget would rise more than that of the larger one.
The equation that connects the amount of heat, Q, and the resulting temperature change, ∆T, is
Q = mc ∆T
where m is the mass of the sample and c is an intrinsic property of the substance called its specific heat. Notice that positive Q is interpreted as heat coming in (∆T is positive, so T increases), while negative Q corresponds to heat going out (∆T is negative, so T decreases).
![]()
2. Gold has a specific heat of 130 J/kg•°C, and wood has a specific heat of 1,800 J/kg•°C. If a piece of gold and a piece of wood, each of mass 0.1 kg, both absorb 2,340 J of heat, by how much will their temperatures rise?
Here”s How to Crack It
We”re given c, m, and Q, and we know that ∆T = Q/(mc).

Celsius vs. Kelvin
Since temperature
measured in Kelvins is
equal to temperature
measured in Celsius plus a
constant, ∆T in Kelvins is
the same as ∆T in Celsius.
Notice that the temperature of gold increased by 180°C, but the temperature of the wood increased by only 13°C.
![]()
![]()
3. A block of Teflon of mass 0.05 kg at a temperature of 430°C is placed in a beaker containing 0.5 kg of water (10 times the mass of the Teflon block) at room temperature, 20°C. After a while, the Teflon and water reach thermal equilibrium (they”re at the same temperature). If the specific heat of water is 4 times the specific heat of Teflon, what”s the common final temperature of the Teflon and the water?
Here”s How to Crack It
Heat always flows from hot to cold. Therefore, when the hot block of Teflon is placed in the cool water, the Teflon loses heat and the water absorbs it. If we let Tf be the final temperature of both the Teflon and the water, then
Qlost by Teflon = mTefloncTeflon(Tf – 430°C)
and
Qgained by water = mwatercwater(Tf – 20°C)
By conservation of energy (ignoring the heat transfer to the air or the beaker), the heat lost by the Teflon is equal to the heat absorbed by the water. Since Qlost by Teflon is heat going out, it”s negative, and since Qgained by water is heat coming in, it”s positive. To account for the signs, we have to write
Qlost by Teflon = –Qgained by water
so

Notice how little the temperature of the water changed. Water has a very high specific heat and can absorb large amounts of thermal energy without undergoing much of a temperature change. We could have used this same experiment to determine the specific heat of Teflon. Drop a known mass of Teflon at a given temperature into the water and then measure the temperature of the water once thermal equilibrium is reached. Knowing this final temperature, we could solve for cTeflon.
![]()
Calorimetry II: Heat Transfer and Phase Changes
Remember that when an object absorbs or loses heat, either its temperature will change or the phase of the object will start to change, but not both. For example, if we start heating an ice cube that”s at 0°C, the heat causes the ice cube to melt, but the temperature remains at 0°C throughout the melting process. Only when the ice cube has completely melted will any additional heat cause the temperature to rise.
The equation that applies during the melting of the ice cube (or during any other phase transition) is the following:
Q = mL
where L is the latent heat of transformation.
This equation tells us how much heat must be transferred to cause a sample of mass m to completely undergo a phase change. In the case of a solid-to-liquid (or vice versa) phase change, L is called the latent heat of fusion. For a phase change between liquid and vapor, L is called the latentheat of vaporization.
![]()
4. The heat of fusion for water is 334 kJ/kg. How much thermal energy is required to completely melt a 100-gram ice cube?
Here”s How to Crack It
The change in phase from solid to liquid requires the input of heat; in this case, Q = mL = (0.1 kg)(334 kJ/kg) = 33.4 kJ.
![]()
![]()
5. A beaker contains 0.1 kg of water, initially at room temperature (20°C). If the specific heat of water is 4.2 J/kg × °C and the latent heat of vaporization is 2,300 kJ/kg, how much thermal energy would the water need to absorb to turn completely to steam?
Here”s How to Crack It
First we need to heat the water to the boiling point, 100°C; then we need to continue to add heat until all the liquid is vaporized. The amount of thermal energy required for the first step is
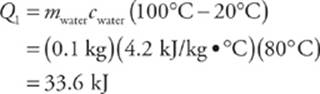
and the amount of energy required for the second step is
Q2 = mwaterLvap = (0.1 kg)(2,300 kJ/Kg) = 230 kJ
Therefore, the total amount of thermal energy required is
Qtotal = Q1 + Q2 = 33.6 kJ + 230 kJ = 264 kJ
![]()