SAT Physics Subject Test
Chapter 15 Thermal Physics
THERMAL EXPANSION
When a substance undergoes a temperature change, it changes in size. Steel beams that form railroad tracks expand when they get warmer; a balloon filled with air shrinks when it”s placed in a freezer. The change in size of a substance due to a temperature change depends on the amount of the temperature change and the identity of the substance.
Let”s first talk about changes in length (of the steel beam, for example). When its temperature is T0, its length is L0. Then, if its temperature changes to Tf, the length changes to Lf, such that
Lf – L0 = αLi(Tf – T0)
where α is the coefficient of linear expansion of the material. This equation is usually used in the simpler form
∆L = αL0 ∆T
Nearly all substances have a positive value of α, which means that they expand upon heating.
6. A steel beam used in the construction of a bridge has a length of 30.0 m when the temperature is 15°C. On a very hot day, when the temperature is 35°C, how long will the beam be? (The coefficient of linear expansion for structural steel is +1.2 × 10–5/°C.)
Here”s How to Crack It
The change in length of the beam is
∆L = α L0∆T =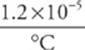 
(30.0 m)(35°C – 15°C) = 7.2 × 10–3 m = 7.2mm
As we”ve mentioned, substances also undergo volume changes when heat is lost or absorbed. The change in volume, ∆V, corresponding to a temperature change, ∆T, is given by the equation
∆V = βV0 ∆T
where V0 is the sample”s initial volume and β is the coefficient of volume expansion of the substance. Since we”re now looking at the change in a three-dimensional quantity (volume) rather than a one-dimensional quantity (length), for most solids, β ≈ 3α. Nearly all substances have a positive value of β, which means they expand upon heating. An extremely important example of a substance with a negative value of β is liquid water between 0°C and 4°C. Unlike the vast majority of substances, liquid water expands as it nears its freezing point and solidifies (which is why ice has a lower density and floats in water).
7. The mercury in a household glass-tube thermometer has a volume of 500 mm3 (= 5.0 × 10–7 m3) at T = 19°C. The hollow column within which the mercury can rise or fall has a cross-sectional area of 0.1 mm2 (= 1.0 × 10–7 m2). Ignoring the volume expansion of the glass, how much will the mercury rise in the thermometer when its temperature is 39°C ? (The coefficient of volume expansion of mercury is 1.8 × 10–4/°C.)
Here”s How to Crack It
First let”s figure out by how much the volume of the mercury increases.
∆V = βV0∆T =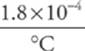 
(5.0 × 10–7 m3)(39°C–19°C) = 1.8 × 10–9 m3
Now, since volume = cross-sectional area × height, the change in height of the mercury column will be
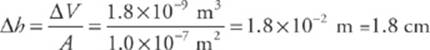
