SAT Physics Subject Test
Chapter 15 Thermal Physics
THE LAWS OF THERMODYNAMICS
We”ve learned about two ways in which energy can be transferred between a system and its environment. One is work, which takes place when a force acts over a distance. The other is heat, which takes place when energy is transferred due to a difference in temperature. The study of the energy transfers involving work and heat, and the resulting changes in internal energy, temperature, volume, and pressure is called thermodynamics.
The Zeroth Law of Thermodynamics
When two objects are brought into contact, heat will flow from the warmer object to the cooler one until they reach thermal equilibrium. This property of temperature is expressed by the zeroth law of thermodynamics.
If objects 1 and 2 are each in thermal equilibrium with object 3, then objects 1 and 2 are in thermal equilibrium with each other.
The First Law of Thermodynamics
Simply put, the first law of thermodynamics is a statement of the conservation of energy that includes heat.
Energy (in the form of heat) is neither created nor destroyed in any thermodynamic system.
The mathematical equation that corresponds to this law is
∆U = Q – W
Where ∆U is the change in internal energy of the system, Q is the heat added to the system, and W is the work done by the system. U depends on the state of the system.
Consider the following example. An insulated container filled with an ideal gas rests on a heat reservoir (something that can act as a heat source or a heat sink). The container is fitted with a snug, but frictionless, weighted piston that can be raised or lowered. The confined gas is the system, and the piston and heat reservoir are the surroundings.
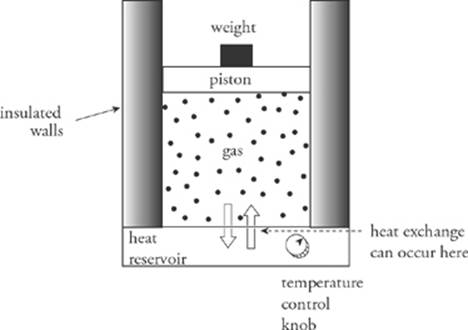
The state of the gas is given once its pressure, volume, and temperature are known, and the equation that connects these state variables is the ideal gas law, PV = nRT. We”ll imagine performing different experiments with the gas, such as heating it or allowing it to cool, increasing or decreasing the weight on the piston, and so on, and study the energy transfers (work and heat) and the changes in the state variables. If each process is carried out such that at each moment, the system and its surroundings are in thermal equilibrium, we can plot the pressure (P) versus the volume (V) on a diagram. By following the path of this P–V diagram, we can study how the system is affected as it moves from one state to another.
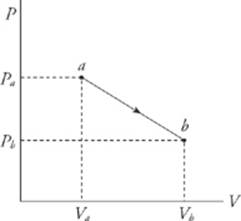
Work is done on or by the system when the piston is moved and the volume of the gas changes. For example, imagine that the gas pushes the piston upward, causing an increase in volume. The work done by the gas during its expansion is W = F∆s, but since F = PA, we have W = PA∆s, and because A∆s = ∆V, we have
W = P∆V
This equation is also true if the piston is pushed down and the volume of the gas decreases. In this case, ∆V is negative, so W is negative. In general, then, W is positive when the system does work against its surroundings, and W is negative when the surroundings do work on the system.
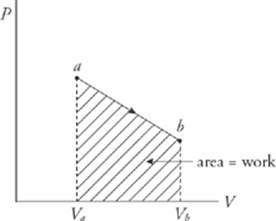
The equation W = P∆V assumes that the pressure P does not change during the process. If P does change, then the work is equal to the area under the curve in the P–V diagram; moving left to right gives a positive area (and positive work), while moving right to left gives a negative area (and negative work).
![]()
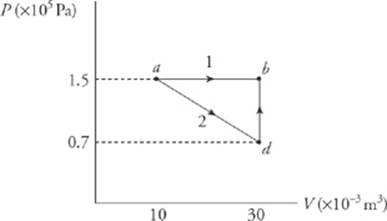
11. What”s the value of W for the process ab following path 1 and for the same process following path 2, shown in the P–V diagram below?
Here”s How to Crack It
Path 1. Since, in path 1, P remains constant, the work done is just P∆V.
W = P∆V = (1.5 × 105 Pa)[(30 × 10–3 m3) – (10 × 10–3 m3)] = 3,000 J
Path 2. If the gas is brought from state a to state b, along path 2, then work is done only along the part from a to d. From d to b, the volume of the gas does not change, so no work can be performed. The area under the graph from a to d is
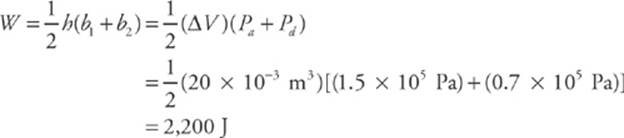
As this example shows, the value of W depends not only on the initial and final states of the system, but also on the path between the two. In general, different paths give different values for W.
![]()
![]()
Questions 12-13
For the previous P–V diagram,
12. Find the work done by the system for the path abda.
13. Find the heat absorbed by the system along this same path.
Here”s How to Crack It
12. From the previous problem, we learned that, for the process ab, W = 3,000 J and for process bd, W = 0. Since W = 2,200 J for the process ad, then W for da would be –2,200 J (∆V is negative.) Therefore, the total W = 3,000 J – 2,200 J = 800 J.
13. Since U depends on the state of the system, for any closed path on a P–V diagram ∆U = 0. Since ∆U = Q – W, we have 0 = Q – 800 J, therefore Q = 800 J.
![]()
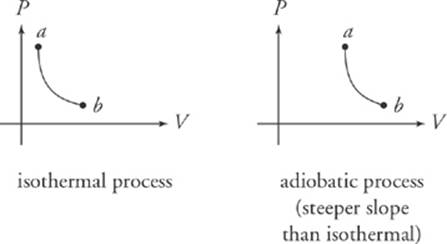
A process where the temperature remains constant is referred to as isothermal. If there is no heat exchanged between the system and its surroundings, the process is adiabatic.
The Second Law of Thermodynamics
Entropy
Consider a box containing two pure gases separated by a partition. What would happen if the partition were removed? The gases would mix, and the positions of the gas molecules would be random.
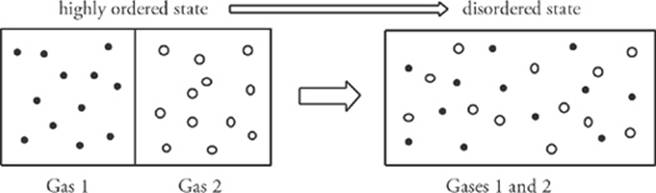
A closed system that shows a high degree of order tends to evolve in such a way that its degree of order decreases. In other words, disorder (or, as it”s technically called, entropy) increases. If we started with the box on the right, containing the mixture of the gases, it would be virtually impossible that at any later time all the molecules of Gas 1 would happen to move to the left side of the box and, at the same time, the molecules of Gas 2 would spontaneously move to the right side of the box. If we were to watch a movie of this process, and saw the mixed-up molecules suddenly separate and move to opposite sides of the box, we”d assume that the film was running backward. In a way, the second law of thermodynamics defines the direction of time: Time flows in such a way that ordered systems become disordered. Disordered states do not spontaneously become ordered without any other change taking place. The following is the essence of one form of the second law of thermodynamics:
The total amount of disorder—the total entropy—of a system plus its surroundings will never decrease.
Now, it is possible for the entropy of a system to decrease, but it”ll always be at the expense of a greater increase in entropy in the surroundings. For example, when water freezes, its entropy decreases. The molecules making up an ice crystal have a more structured order than the random collection of water molecules in the liquid phase, so the entropy of the water decreases when it freezes. But when water freezes, it releases heat energy into its environment, which creates disorder in the surroundings. If we were to figure out the total change in entropy of the water plus its surroundings, we”d find that although the entropy of the water itself decreased, it was more than compensated by a greater amount of entropy increase in the surroundings. So, the total entropy of the system and its surroundings increased, in agreement with the second law of thermodynamics.
There are several equivalent statements of the second law. In addition to the entropy form, another form says that heat always flows from an object at higher temperature to an object at lower temperature, never the other way around. Heat always flows from hot to cold, never cold to hot. Another form, which will be considered more fully in a moment, says that a heat engine can never operate at 100% efficiency, or, equivalently, that it is impossible to convert heat completely into work.
Efficiency of Heat Engines
Converting work to heat is easy—rubbing your hands together shows that work can be converted to heat. What we”ll look at now is the reverse process: How efficiently can heat be converted into work? A device that uses heat to produce useful work is called a heat engine. The internal-combustion engine in a car is an example. Certain types of engines take their working substance (a mixture of air and fuel in the case of a car engine) through a cyclic process, so that the cycle can be repeated. The basic components of any cyclic heat engine are simple: Energy in the form of heat comes into the engine from a high-temperature source, some of this energy is converted into useful work, the remainder is ejected as exhaust heat into a low-temperature sink, and the system returns to its original state to run through the cycle again.
Since we”re looking at cyclic engines only, the system returns to its original state at the end of each cycle, soU must be 0. Therefore, by the first law of thermodynamics, Q net = W. So, the net heat absorbed by the system is equal to the work performed by the system. The heat that”s absorbed from the high-temperature source is Q H (H for hot), and the heat that is discharged into the low-temperature reservoir is Q C (C for cold). Because heat coming in is positive and heat going out is negative, Q H is positive and Q C is negative, and the net heat absorbed is QH + Q C. Instead of writing Q net in this way, we usually write it as QH – |QC|, to show that Q net is less than Q H. The thermal efficiency, e, of the heat engine is equal to the ratio of what we get out to what we have to put in—that is, e = QW/QH. Since W = Qnet = QH – |QC|, we have
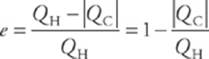
Notice that unless QC = 0, the engine”s efficiency is always less than 1. Here is another form of the second law of thermodynamics.
For any cyclic heat engine, some exhaust heat is always produced. Because QC ≠ 0, no cyclic heat engine can operate at 100% efficiency; it is impossible to completely convert heat into useful work.
![]()
14. A heat engine draws 800 J of heat from its high-temperature source and discards 600 J of exhaust heat into its cold-temperature reservoir each cycle. How much work does this engine perform per cycle, and what is its thermal efficiency?
Here”s How to Crack It
The work output per cycle is equal to the difference between the heat energy drawn in and the heat energy discarded.
W =QH – |QC| = 800 J – 600 J = 200 J.
The efficiency of this engine is
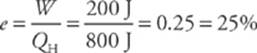
![]()
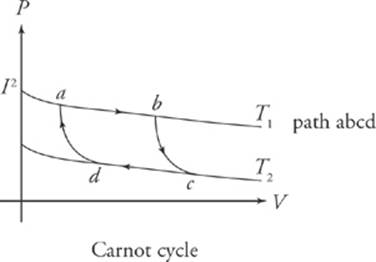
The Carnot Cycle
The most efficient heat engine follows what is known as the Carnot cycle: isothermal expansion, followed by adiabatic expansion, followed by isothermal compression, followed by adiabatic compression.
For the Carnot cycle, efficiency can be written as
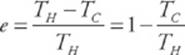
where TH and TC are temperatures of the hot and cold reservoirs, respectively.