SAT Physics Subject Test
Chapter 16 Modern Physics
PHOTONS AND THE PHOTOELECTRIC EFFECT
The particle-like nature of light was revealed and studied through the work of Max Planck in 1900, and later Albert Einstein (who won the 1921 Nobel prize for work in this area). Electromagnetic radiation is emitted and absorbed by matter as though it existed in individual bundles calledquanta. A quantum of electromagnetic energy is known as a photon. Light behaves like a stream of photons, and this is illustrated by the photoelectric effect.
When a piece of metal is illuminated by electromagnetic radiation (either visible light, ultraviolet light, or X-rays), the energy absorbed by electrons near the surface of the metal can liberate them from their bound state, and these electrons can fly off. The released electrons are known asphotoelectrons. In this case, the classical, wave-only theory of light would predict the following three results:
(1) There would be a significant time delay between the moment of illumination and the ejection of photoelectrons, as the electrons absorbed incident energy until their kinetic energy was sufficient to release them from the atoms” grip.
(2) Increasing the intensity of the light would cause the electrons to leave the metal surface with greater kinetic energy.
(3) Photoelectrons would be emitted regardless of the frequency of the incident energy, as long as the intensity was high enough.
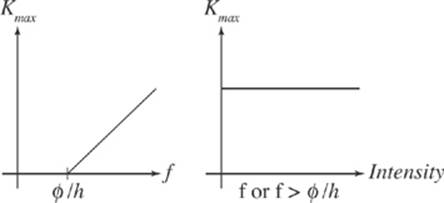
Surprisingly, none of these predictions was observed. Photoelectrons were ejected within just a few billionths of a second after illumination, disproving prediction (1). Secondly, increasing the intensity of the light did not cause photoelectrons to leave the metal surface with greater kinetic energy. Although more electrons were ejected as the intensity was increased, there was a maximum photoelectron kinetic energy; prediction (2) was false. And, for each metal, there was a certain threshold frequency, f0: If light of frequency lower than f0 were used to illuminate the metal surface, no photoelectrons were ejected, regardless of how intense the incident radiation was; prediction (3) was also false. Clearly, something was wrong with the wave-only theory of light.
Einstein explained these observations by postulating that the energy of the incident electromagnetic wave was absorbed in individual bundles (photons).

The energy of a photon is proportional to the frequency of the wave,
E = hf
where h is Planck”s constant (about 6.63 10–34 J·s).
A certain amount of energy had to be imparted to an electron on the metal surface in order to liberate it; this was known as the metal”s work function, or Ø. If an electron absorbed a photon whose energy E was greater than Ø, it would leave the metal with a maximum kinetic energy equal toE – Ø. This process could occur very quickly, which accounts for the rapidity with which photoelectrons are produced after illumination.
Kmax = hf – Ø
Increasing the intensity of the incident energy means bombardment with more photons and results in the ejection of more photoelectrons—but since the energy of each incident photon is fixed by the equation E = hf, the value of Kmax will still be E – Ø. This accounts for the observation that disproved prediction (2).
Finally, if the incident energy had a frequency that was less than Ø/h, the incident photons would each have an energy that was less than Ø; this would not be enough energy to liberate electrons. Blasting the metal surface with more photons (that is, increasing the intensity of the incident beam) would also do nothing; none of the photons would have enough energy to eject electrons, so whether there were one or one million wouldn”t make any difference. This accounts for the observation of a threshold frequency, which we now know is Ø/h.
Before we get to some examples, it”s worthwhile to introduce a new unit for energy. The SI unit for energy is the joule, but it”s too large to be convenient in the domains we”re studying now. We”ll use a much smaller unit, the electronvolt (abbreviated eV). The eV is equal to the energy gained (or lost) by an electron accelerated through a potential difference of one volt. Using the equation ∆UE = q∆V, we find that
1 eV = (1 e)(1 V) = (1.6 × 10–19 C)(1 V) = 1.6 Ø 10–19 J
In terms of electronvolts, the value of Planck”s constant is 4.14 × 10–15 eV•s.
![]()
Questions 1-3
The work function for a certain metal is 4.14 eV.
1. What is the threshold frequency required to produce photoelectrons from this metal?
2. To what wavelength does the frequency in Question 1 correspond?
3. Light with frequency 2 × 1015 Hz is directed onto the metal surface. Describe what would happen to the number of photoelectrons and their maximum kinetic energy if the intensity of this light were increased by a factor of 2.
Here”s How to Crack It
1. We know from the statement of the question that for a photon to be successful in liberating an electron from the surface of the metal, its energy cannot be less than 4.14 eV. Therefore, the minimum frequency of the incident light—the threshold frequency—must be
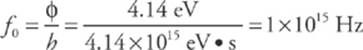
2. From the equation λf = c, where c is the speed of light, we find that
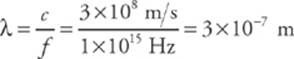
3. Since the frequency of this light is higher than the threshold frequency, photoelectrons will be produced. If the intensity (brightness) of this light is then increased by a factor of 2, that means the metal surface will be hit with twice as many photons per second, so twice as many photoelectrons will be ejected per second. Thus, making the incident light brighter releases more photoelectrons. However, their maximum kinetic energy will not change. The only way to increase Kmax is to increase the frequency—not the brightness—of the incident light.
![]()