SAT For Dummies
Part IV
Take a Number, Any Number: The Mathematics Sections
Chapter 15
Practicing Problems in Algebra and Functions
In This Chapter
![]() Practicing algebra and functions with some guided problems
Practicing algebra and functions with some guided problems
![]() Troubleshooting your problem areas with some independent-practice questions
Troubleshooting your problem areas with some independent-practice questions
In this chapter, you hone your skills for SAT algebra and function problems. Try ten, see how you do, and then try ten more if you’re a glutton for punishment (or algebra, which in some people’s minds is the same thing).
Be sure to check all your answers against mine. Don’t neglect the explanations, which may help you understand what went wrong. In the first practice set, each answer immediately follows the question. Don’t cheat. Cover the answer with a piece of paper until you’re ready to read the explanation. The second set is set up like the real test: You go through all the questions and then check your answers in the next section. For more information on any of the topics I cover in these practice questions, check out Chapter 14.
Set 1: Getting Started with Some Guided Questions
Note: Question 3 is a grid-in, so you don’t get any answers to choose from. See Chapter 11 for details on answering grid-ins correctly.
1. If k is a positive integer, which of the following is a possible value for k2?
(A) –1
(B) 0
(C) 2
(D) 6
(E) 9
Choice (A) is impossible because any number, when squared, is positive. Choice (B) is zero squared, but the problem said that the original number had to be positive. Choices (C) and (D) aren’t perfect squares; no number multiplied by itself gives you 2 or 6 as an answer. That leaves you with (E), which is 32.
2. If ![]() , then increasing the value of y by 2 will increase x by
, then increasing the value of y by 2 will increase x by
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
This problem is good for picking your own numbers. For example, say that y was originally
10; then you would have ![]() . Multiplying both sides by 2 gives you 20 = x + 5, or x = 15.
. Multiplying both sides by 2 gives you 20 = x + 5, or x = 15.
Now the problem tells you to increase y by 2, making it 12. If you do the math (I’m trusting you here), you find that x is now 19, so it increased by 4. This result makes sense because the equation tells you that you need to divide x + 5 by 2 to get y; y increases half as quickly as x. Thus, your answer is (D).
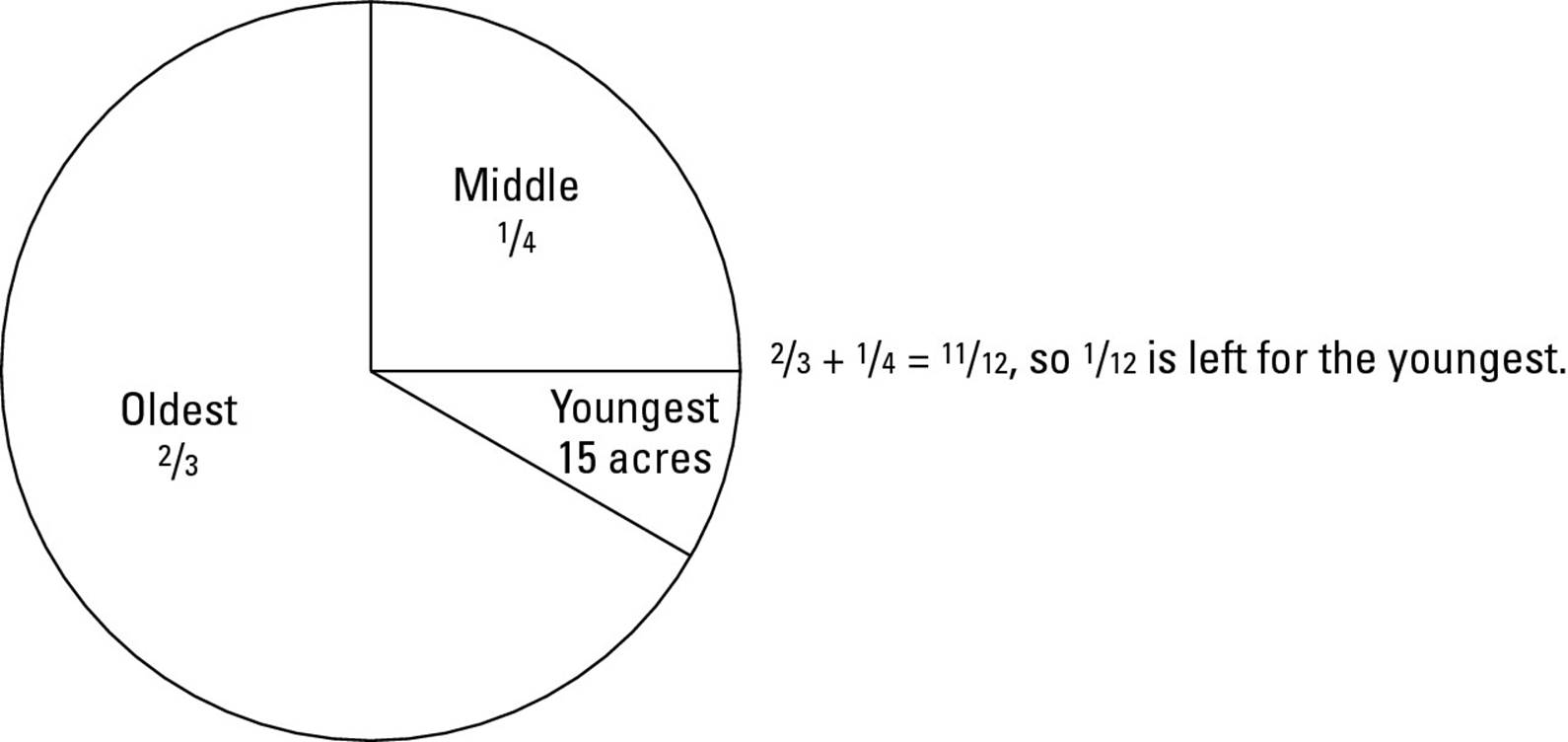
3. In his will, a man left his land to his three children: 2⁄3 of the estate to his oldest child, 1⁄4 to his middle child, and 15 acres to his youngest. How many acres were in the original estate?

A word problem? With no multiple-choice answers? And fractions? Okay, deep breaths. Now get to work. In any word problem, list the various things you need to know to solve the problem. Four important things pop up in this one: the original estate and the amount left to the three children. Because the original estate is what you’re looking for, call it x. Remembering that the word of usually indicates multiplication, you can then make a list:
x = original estate
![]() = oldest child
= oldest child
![]() = middle child
= middle child
15 = youngest child
Because the three children’s shares made up the whole estate, you can write
![]() .
.
With a common denominator of 12:
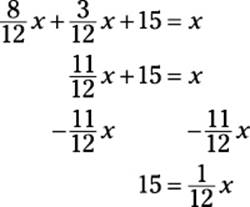
Finally, multiplying both sides by 12, you get x = 180.
That’s a lot of work for one problem. If you’re a visual person, you may prefer to solve it with a graph:
4. If x and y are both integers, x > 3, and y < 2, then x – y could be
(A) 3
(B) 2
(C) 1
(D) 0
(E) –1
After the last problem, this one’s a breeze. x is an integer greater than 3, so it must be at least 4. y is an integer less than 2, so it must be at most 1. 4 – 1 = 3, so (A) is correct. Notice that making x bigger or y smaller would make x – y bigger than 3, so all the other choices are impossible.
5. If n and p vary directly, and n = 12 when p = 9, which of the following pairs is a possible set of values for n and p?
(A) n = 9, p = 12
(B) n = 18, p = 15
(C) n = 18, p = 6
(D) n = 20, p = 15
(E) n = 10, p = 8
When quantities vary directly, their ratio — in this case n⁄p — must always remain the same. There are two ways to solve this problem. One way is to set up the ratios one at a time, cross-multiplying to see which answer works. For example, for (A), write 12⁄9 = 9⁄12. Cross-multiplying gives you 144 = 81, so this answer doesn’t work. Repeating this process shows that (D) works.
The other way to solve this problem is to find the original ratio on your calculator. 12⁄9 = 1.3333 . . . or 4⁄3. Trying all the other pairs shows you that only 20⁄15 gives you the same ratio.
6. If a2– b2 = 40 and a – b = 10, then a + b =
(A) 4
(B) 10
(C) 14
(D) 30
(E) It cannot be determined from the information given.
Well, (E) sure looks tempting, but you can do better. When you see a quadratic expression in a problem, see if it can be factored. a2 – b2 should look familiar to you. (If not, turn to Chapter 14.) Keep in mind that a2 – b2 factors out to (a – b)(a + b). Because a2 – b2 = 40 and a – b = 10, (10)(a + b) = (40), so a + b = 4. Notice that you didn’t even have to figure out the value of the variables to solve the problem; that situation actually happens a lot on the SAT. Three cheers for (A).
7. A copying service charges $2.50 to copy up to 20 pages, plus 5 cents per page over 20. Which formula represents the cost, in dollars, of copying c pages, where c is greater than 20?
(A) 2.50 + 5c
(B) 2.50 + 0.05c
(C) (2.50)(20) + 0.05c
(D) 2.50 + 0.05(c – 20)
(E) 0.05(2.50 + c)
As is often the case, one good approach is to pick a number for c and then see which formula works. Try c = 28. (Remember, c has to be greater than 20). The cost for 28 pages would be $2.50 for the first 20, plus $0.05 times the 8 remaining pages, which is $0.40, for a total of $2.90. Plugging 28 into the various formulas (using a calculator, of course) yields $142.50 for (A), $3.90 for (B), $51.40 for (C), $2.90 for (D), and $1.53 for (E). Choice (D) is correct.
8. Let a be defined as one more than a if a is odd, and as one less than a if a is even. Which of the following would result in the smallest number?
(A) –2
(B) –1
(C) 0
(D) 1
(E) 2
Test out each answer choice. Choice (A), –2, is even, so one less than –2 is –3. The other choices give you 0, –1, 2, and 1, in that order. Thus, Choice (A) is correct.
9. If (2g – 3h)3 = 27, then (2g – 3h)–2 =
(A) 9
(B) 1⁄6
(C) 1⁄9
(D) –6
(E) –9
First, give up on trying to figure out the values of g and h. The key is the expression (2g – 3h), which shows up in both parts of the problem. Replace it with something simpler, like q. (I get tired of using x all the time.) So you know that q3 = 27. A little trial and error (or your
calculator) reveals that q = 3. Now you need to find 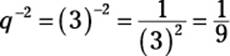 . Choice (C) is correct.
. Choice (C) is correct.
10. A party supplier charges a flat rate, plus a certain amount for each person. If supplies for 12 people cost $140, and supplies for 20 people cost $180, then supplies for 40 people would cost
(A) $220
(B) $280
(C) $300
(D) $360
(E) $400
The setup for this problem is a classic linear equation. The flat rate is the y-intercept, while the amount per person is the slope. Therefore, you can write y = mx + b, using the number of people as x and the cost as y. When you’re solving a problem like this, find the slope first,
using the formula ![]() . Bingo, the cost per person is $5. You can
. Bingo, the cost per person is $5. You can
now figure out b by using either pair of numbers. Because supplies for 12 people cost $140, and $5 × 12 people = $60, the flat rate is $80. (You’d get the same answer if you used 20 people and $180.) Your equation is y = 5x + 80. Plugging in 40 for x gives you y = 280. Choice (B) is correct.
By the way, another way to do this problem is to play “find the pattern.” When the number of people went up by 8 — from 12 to 20 — the cost went up by $40. You could make a chart like this one:
![]()
The cost for 40 people would be halfway between $260 and $300 — in other words, $280.
Set 2: Practicing Some Questions on Your Own
Note: Question 1 is a grid-in. Turn to Chapter 11 for help on answering that type of question.
1. If (x + 2)2 + (x – 1)2 = ax2 + bx+ c, find the value of b.

2. The pressure of a gas and its volume vary inversely. If a certain gas has a pressure of 120 kilopascals (kPa) when its volume is 250 cubic centimeters (cc), what is its pressure when its volume is 200 cc?
(A) 170 kPa
(B) 150 kPa
(C) 100 kPa
(D) 96 kPa
(E) 70 kPa
3. Given the function ![]() ,
,
which number is not a possible value for x?
(A) –4
(B) –2
(C) 0
(D) 2
(E) 4
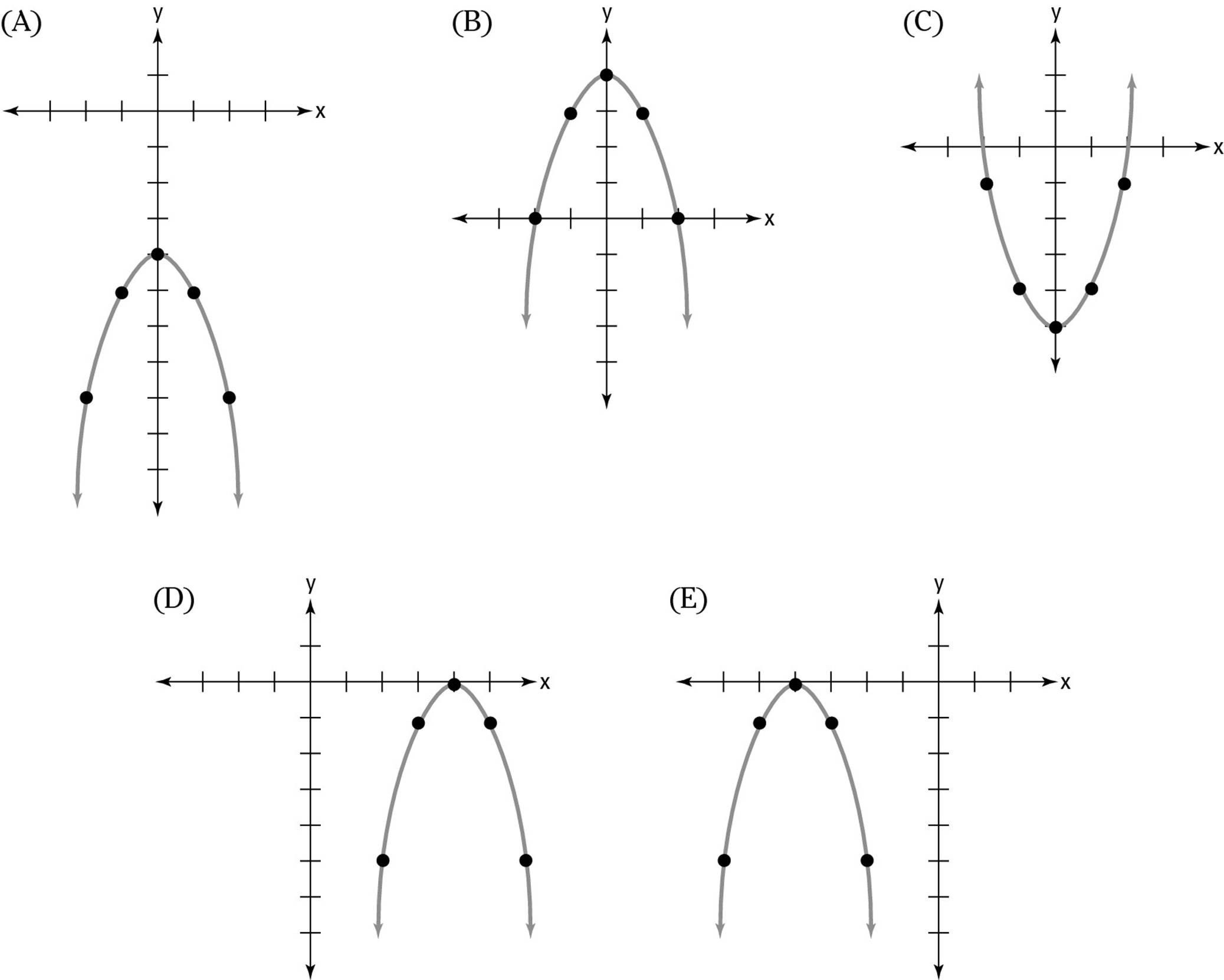
4. Below is the graph of the equation y = –x2.
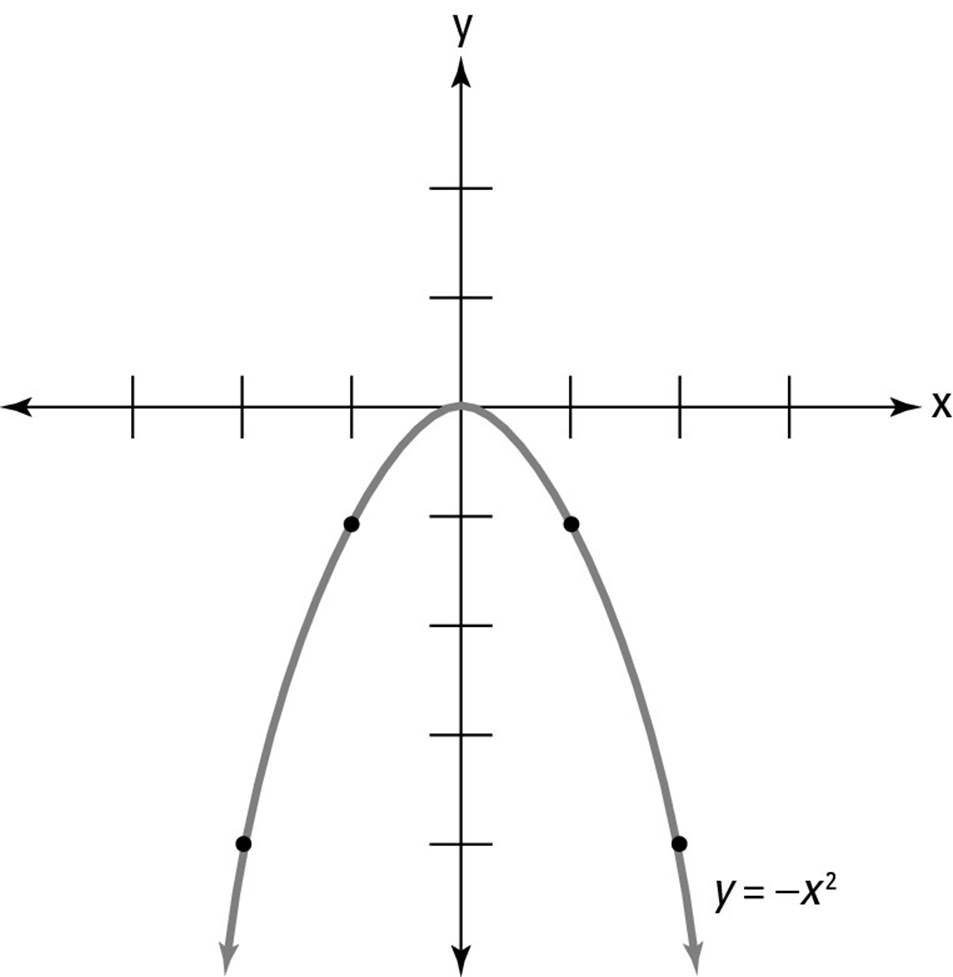
Which of the following choices represents the graph of y = –x2 + 4?
5. The solution set to the equation ![]() is
is
(A) {6}
(B) {6, –6}
(C) {–6}
(D) {–2, –6}
(E) {–2}
6. If f(x) is a linear function passing through the points (2, 5) and (6, 3), then the y-intercept of f(x) is
(A) 7
(B) 6
(C) 5
(D) 4
(E) 3
7. If x\\y is defined as x2 – y, which statement is always true?
(A) 0\\y = y
(B) x\\1 is positive
(C) x\\4 = x\\(–4)
(D) x\\y = y\\x
(E) 4\\y = (–4)\\y
8. If k1/2 – 3 = 5, then k =
(A) 64
(B) 16
(C) 8
(D) 4
(E) 2
9. The population of a certain city can be modeled by the function p(y) = 20,000(2)y/20, where p(y) represents the population, and y measures years since 1976. If the city had a population of 32,490 in 1990, then its population in 2030 will be
(A) 30,000
(B) 64,980
(C) 80,000
(D) 108,000
(E) 129,960
10. The solution set to the equation
![]() is
is
(A) { }
(B) {–1}
(C) {–1, 2}
(D) {2}
(E) {8}
Answers to Set 2
1. 2. The answer is 2. This problem is an easy one to mess up, but not if you remember the formulas I explain in Chapter 14: (a + b)2 = a2 + 2ab + b2. It’s also fine to just do FOIL, rewriting the problem as (x + 2)(x + 2) + (x – 1)(x – 1). Either way, the problem becomes x2 + 4x + 4 + x2– 2x + 1, which equals 2x2 + 2x + 5, so b = 2.
2. B. When two quantities vary inversely, their product is always the same number. Usually, finding that number is the key to getting the right answer. You’re told that a pressure of 120 corresponds to a volume of 250, and 120 × 250 = 30,000. Thus, your missing pressure (call it p), times 200, must equal 30,000. Solving 200p = 30,000 gives you p = 150. Common-sense double-check: If quantities vary inversely, one of them should go up when the other goes down. Notice that the volume went down from 250 cc to 200 cc and that the pressure went up from 120 kPa to 150 kPa. Whenever possible, take a second to make sure your answer makes sense. Choice (B) is correct.
3. D. In this problem, you know that dividing by 0 is against the rules. The denominator can be factored to (x – 2)(x – 2), which means that 2 is the only number that would make the denominator zero, so it’s the only number that’s not in the domain (the fancy name for “all the possiblex-values”). Choice (D) is correct.
4. B. Adding 4 to a function raises its graph by four units, so Choice (B) is correct.
5. E. You could just plug in all the choices, but, for practice, try to go through the official steps:
Isolate the absolute value: 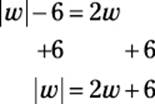
Create two equations: 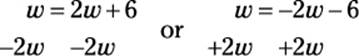
Solve: 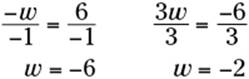
Check: 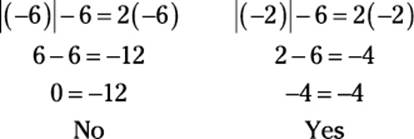
So the only answer that works is –2. Choice (E) is correct.
6. B. If you find a sketch helpful (I know I do), draw something like the following graph:
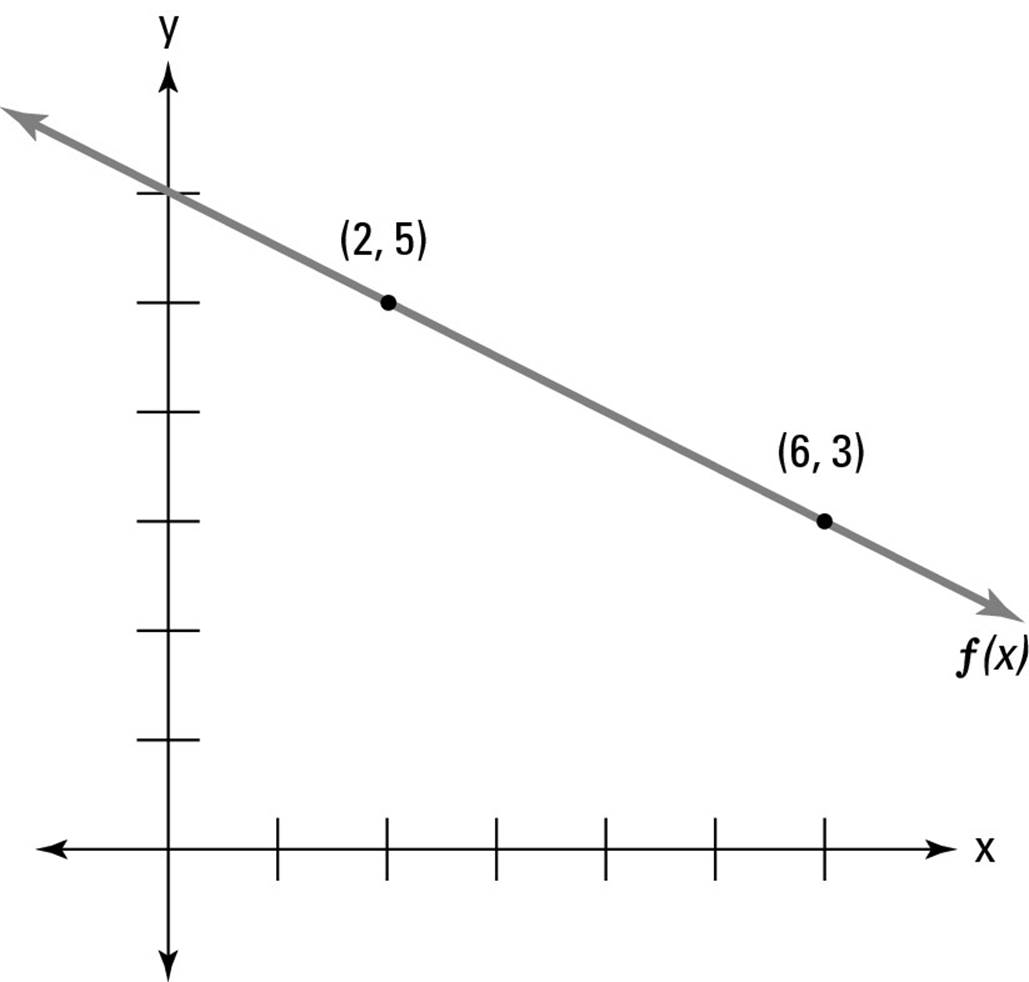
The graph can convince you that the answer is either (A) or (B).To be sure, use your formula for linear equations, y = mx + b. First, find the slope of your line:
![]()
So the equation is y = –1⁄2 x + b. Use (2, 5) to find b:
5 = –1⁄2(2) + b
5 = –1 + b
+1 +1
6 = b
So your y-intercept is 6, and the answer is (B).
7. E. No cool solving methods here. You just have to check all the possibilities.
Choice (A): 0\\y = (0)2 – y = 0 – y = –y. Nope. Onward to (B): x\\1 = (x)2 – 1 = x2 – 1. This is usually positive, but if x is zero (or a fraction), then it’s negative. Moving on to (C): x\\4 = (x)2 – 4 = x2 – 4, and x\\(–4) = (x)2 – (–4) = x2 + 4. They’re not equal. Now for (D): x\\y = x2 – y, andy\\x = y2 – x. These don’t look equal, and plugging in two different numbers for x and y should convince you that they’re not. Which leaves (E): 4\\y = (4)2 – y = 16 – y, and (–4)\\y = (–4)2 – y = 16 – y. At last!
8. A. Here’s the official way to solve the problem:
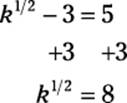
Because k1/2 means ![]() , square both sides:
, square both sides:
k = 82 = 64
So (A) is correct. Of course, you can also just plug in all the choices to see which one works. The key is knowing what k1/2 means.
9. E. When you’re given a problem like this one, it helps to pause for a moment to see whether you can figure out what the function really means. This function is an exponential growth situation. The initial population (in 1976) was 20,000, and the function doubles (the growth factor is 2) every 20 years. If you understand this concept, you can figure out the answer without actually plugging the numbers into the function. Because the population doubles every 20 years, it doubles from 1990 to 2010 and doubles again from 2010 to 2030. 32,490 × 2 × 2 = 129,960, so Choice (E) is correct.
You can also solve the problem by plugging the right numbers into your calculator. Because 2030 – 1976 = 54 years, plug in 54 for y. 20,000(2)54/20 = 20,000(2)2.7 = 20,000(6.4980) = 129,960.
10. D. The best way to do this problem is to start by noticing that the two fractions have common denominators. Therefore, they can be combined if you get them on the same side:
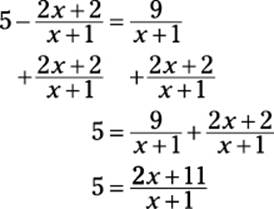
Now, if you multiply by x + 1 on both sides:
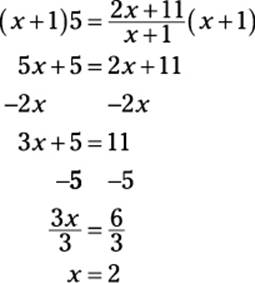
Choice (D) is correct.