SAT For Dummies
Part IV
Take a Number, Any Number: The Mathematics Sections
Chapter 17
Practicing Problems in Geometry
In This Chapter
![]() Practicing a few guided geometry problems
Practicing a few guided geometry problems
![]() Focusing on angles, shapes, and distances in some sample questions
Focusing on angles, shapes, and distances in some sample questions
Even if you’d rather squash a polygon than calculate its measurements, bite the bullet and check out at least some of the practice questions in this chapter. You get two sets. In the first set, move through each problem by solving it and then immediately checking your answer using the explanation I provide. Don’t cheat. Cover the answers with a blank sheet of paper until you come up with your own solutions. If you (gasp) stub your toe on any of these geometry problems, try your hand at the second set, which is set up like the actual test. In that set, solve all the questions before checking your answers with the explanations I offer in the section that follows the questions. (Turn to Chapter 16 for more information on any of the topics covered in these practice questions.)
The following diagrams appear at the beginning of each math section of the SAT to help you work through the geometry problems. Don’t hesitate to use them as you answer the practice problems in this chapter.
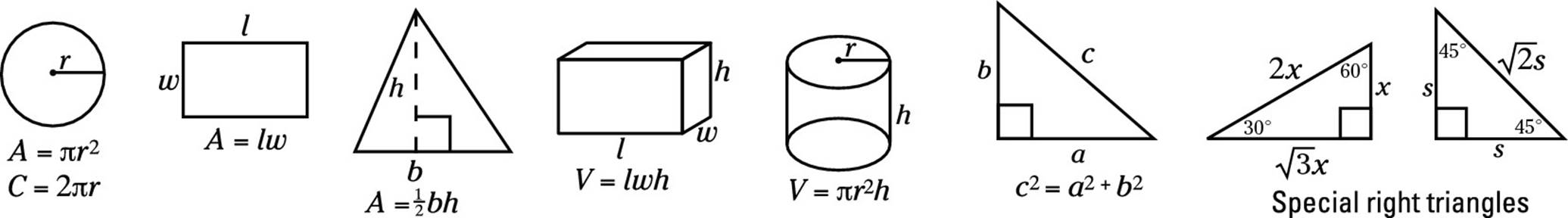
Set 1: Getting Started with Some Guided Questions
Note: Questions 3 and 6 are grid-ins, so you don’t get any answers to choose from. See Chapter 11 for a quick review of grid-ins.
1. In the following square, what is the length of side s?
(A) 8
(B) ![]()
(C) ![]()
(D) 16
(E) ![]()
Choice (A) is correct. When you cut a square in half, you get a 45-45-90 triangle, with the square’s diagonal as the hypotenuse. The freebie information at the beginning of each math section (nice of them to help you, don’t you think?) tells you that in a 45-45-90 triangle, the length of the hypotenuse equals ![]() , where s is the length of a side of the square. Because the hypotenuse equals
, where s is the length of a side of the square. Because the hypotenuse equals ![]() , the side equals 8.
, the side equals 8.
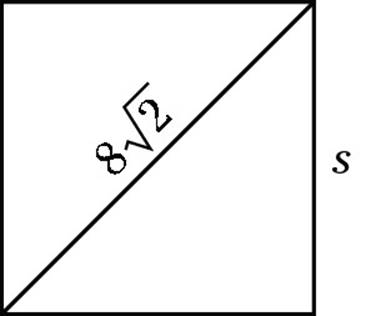
2. If the distance between points A and B is 5, and the distance between points B and C is 7, then the distance between points A and C may not equal
(A) 1
(B) 2
(C) 3
(D) 6
(E) 7
Choice (A) is correct. To answer this question, draw a line connecting A and B and another one connecting B and C, like so:
Now you can use a little thing called the triangle inequality. The distance from A to C forms the third side of a triangle, and a law was made a distant eon ago that the sum of two sides of a triangle must be greater than the third side. That law makes it impossible for AC to equal 1 because 1 + 5 = 6, which isn’t bigger than 7. Before moving on, take a minute to make sure the other four answers do satisfy the triangle inequality (or I’m in a lot of trouble).
 Beware of making assumptions in geometry problems. The first thing to realize when you look at Question 2 is that A, B, and C don’t have to make a straight line, though they could. Most people assume that the three points must be on the same line.
Beware of making assumptions in geometry problems. The first thing to realize when you look at Question 2 is that A, B, and C don’t have to make a straight line, though they could. Most people assume that the three points must be on the same line.
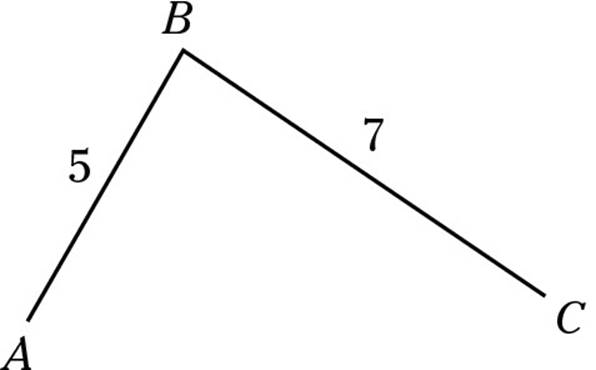
3. In the following drawing, ![]() . Find the measure, in degrees, of the angle marked x.
. Find the measure, in degrees, of the angle marked x.

Because this drawing contains parallel lines cut by transversals (the two lines meeting at point A), you can fill in a whole lot of angles right off the bat. Each transversal creates eight angles, and these angles come in two groups of four equal angles each. Here they are, filled in:
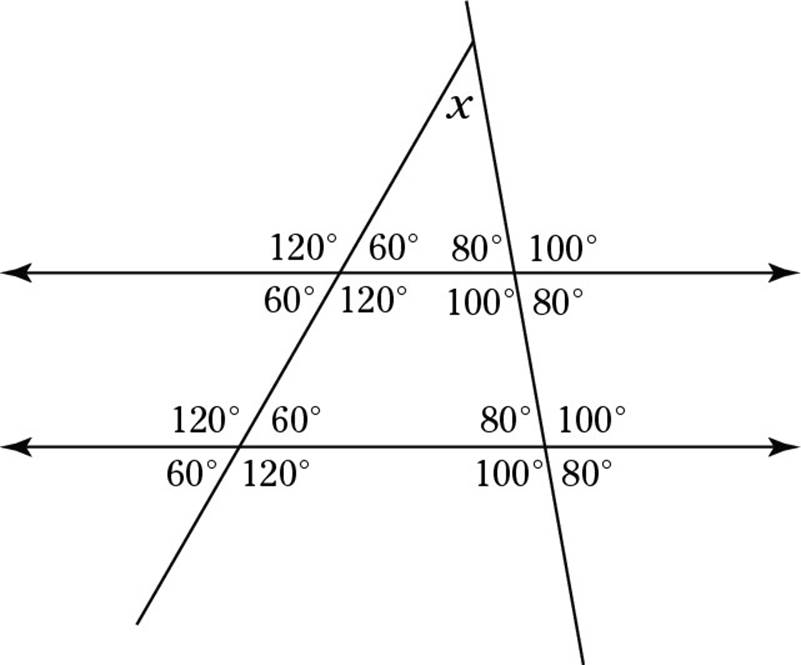
After you determine the angles, the problem becomes simpler. Because ACD is a triangle, its angles must add up to 180 degrees. With a 60-degree and an 80-degree angle already accounted for, the missing angle must be 40 degrees — your correct answer.
 Don’t grid-in the degree symbol; just do the number.
Don’t grid-in the degree symbol; just do the number.
4. What is the sum of the angles marked a, b, c, and d in the following diagram?
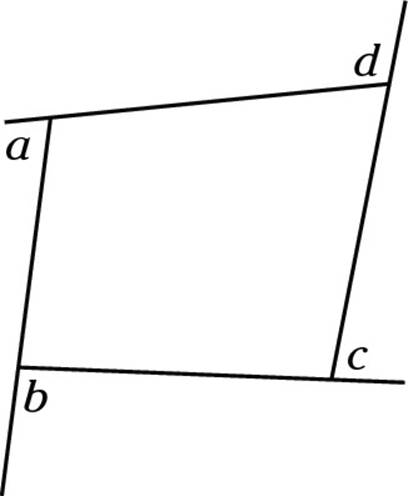
(A) 180 degrees
(B) 360 degrees
(C) 540 degrees
(D) 720 degrees
(E) It cannot be determined from the information given.
Choice (B) is correct. This one you just have to memorize. The sum of the exterior angles of any shape is always 360 degrees. Remember that fact.
5. If an equilateral triangle has sides of length 6, then its altitude has a length of
(A) 3
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Choice (D) is correct. This one’s a special-triangle problem in disguise. Here’s the equilateral triangle with its altitude drawn:
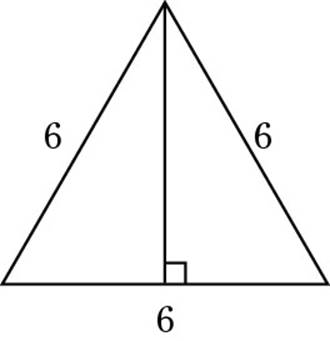
(Of course, you drew this triangle as soon as you were done reading the problem, right?) Each half of the original triangle forms a 30-60-90 triangle. Making a second drawing just to be clear is worth your time.
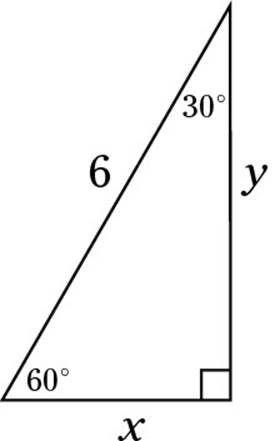
From the formulas I provide at the beginning of this chapter, you know that the side marked x must be half of 6, or 3, which means that y, the altitude, must equal ![]() . Thus, (D) is correct.
. Thus, (D) is correct.
6. In the following diagram, O is the center of the circle, and angles A and B have the same measure. Find the measure of the angle marked x in degrees.
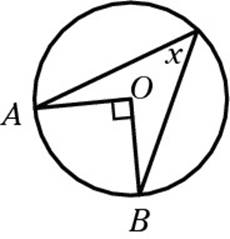

The easiest way to think about this problem is to chop the dart shape in the circle into two triangles, like so:
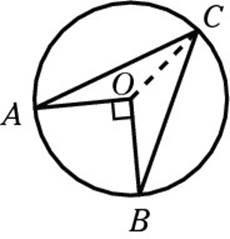
Notice that the line segments OA, OB, and OC are all radii, which makes them all the same length. That means both triangles are isosceles. In any isosceles triangle, the base angles must have equal measures; because you were told that A and B have the same measure, all the angles marked below are congruent:
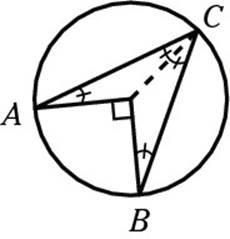
You’re almost to the solution. Because angle AOB is 90 degrees, the other side of the angle (dark line below) must measure 270 degrees to make 360 degrees around a point. That means that half of 270, or 135 degrees, is the top angle of the isosceles triangle. That leaves 45 degrees for the other two angles. And, because two of these angles together made up x, x must equal 45. Whew!
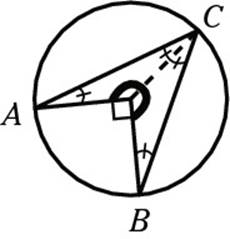
Set 2: Practicing Some Questions on Your Own
Note: Refer to the diagrams I provide at the beginning of this chapter to help you answer these questions. Remember that those diagrams appear at the beginning of the math sections on the real SAT.
1. In this triangle, the measure of angle x is greater than the measure of angle y. Which of the following statements must be false?
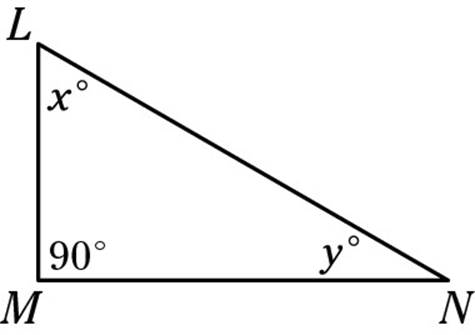
(A) MN > LM
(B) (LN)2 – (LM)2 = (MN)2
(C) LN > MN
(D) LN – LM = MN
(E) ![]()
2. A car has wheels with a radius of 1.5 feet. If the car is backed down a driveway that is 95 feet long, about how many complete turns will the wheels make?
(A) 10
(B) 13
(C) 14
(D) 20
(E) 32
3. In the following diagram, O is the center of the circle, and ![]() and
and ![]() are tangents. If OA = 8 and BP = 9, find CP.
are tangents. If OA = 8 and BP = 9, find CP.
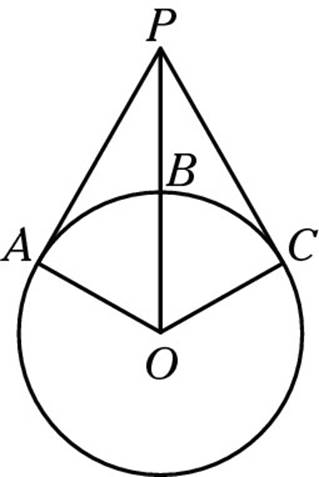
(A) ![]()
(B) 9
(C) ![]()
(D) 15
(E) 17
4. In the following diagram, a square is inscribed in a circle. If one side of the square has a length of 10, then the shaded area equals
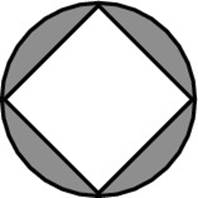
(A) 100π – 100
(B) 50π – 100
(C) 100π – 50
(D) 100 – 25π
(E) 50π – 50
5. In the following drawing, ACDE is a parallelogram with an area of 36. Find the length of AC.
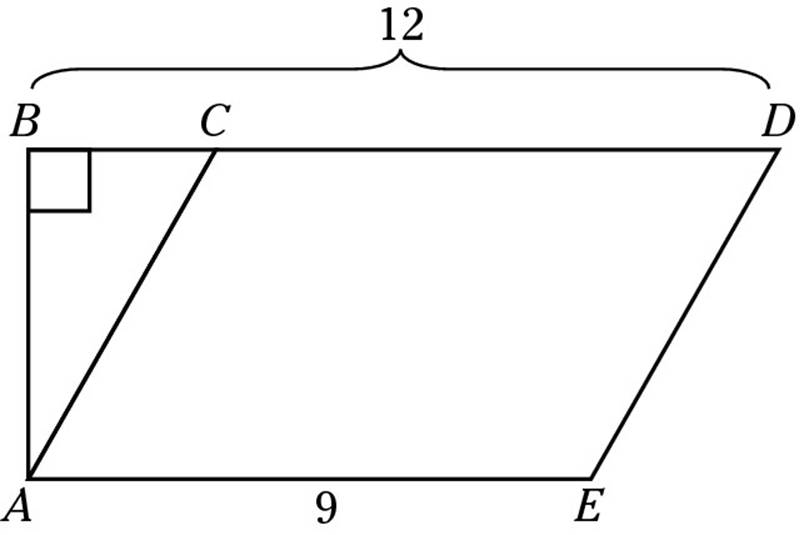
(A) 3
(B) ![]()
(C) 4
(D) 5
(E) ![]()
6. This cylindrical gas tank, originally empty, has a radius of 2 m and a height of 3 m. At 11 a.m., gas starts being added to the tank at a rate of 10 m3 per hour. The tank will be completely full closest to
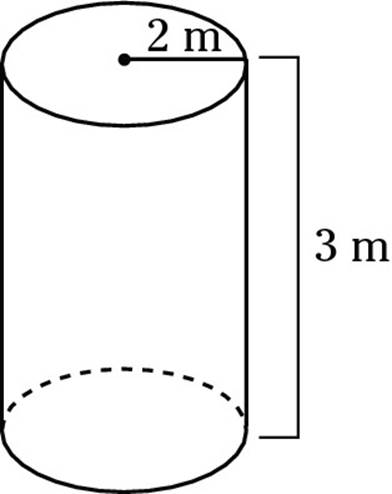
(A) 2 p.m.
(B) 2:30 p.m.
(C) 3 p.m.
(D) 3:30 p.m.
(E) 4 p.m.
Answers to Set 2
1. D. As you often should do in this type of problem, go through the answers one by one. Choice (A) is true because, in any triangle, the shortest side is opposite the smallest angle. Because y is smaller than x and both of them must be smaller than 90 degrees, y is the smallest angle andLM is the shortest side. Choice (B) is just a fancy way of writing the Pythagorean Theorem. Because LN is the hypotenuse of a right triangle, (LM)2 + (MN)2 = (LN)2, so (LN)2 – (LM)2 = (MN)2. Choice (C) is true for essentially the same reason as (A): LN must be the longest side of the triangle because it’s across from 90 degrees, the largest angle. Choice (D) wins the “False Award” because of the triangle inequality. In any triangle, the sum of the two short sides must be greater than the sum of the longest side. That fact means that LM + MN > LN, so LN – LM can’t equal MN. You could stop there, but just to be thorough, check out the last one. Choice (E) is true. Because the sum of the angles of any triangle is 180 degrees, the measures of x and y must add up to 90 degrees. Because x is larger than y, x must be greater than 45 degrees, and y must be less than 45 degrees. The correct answer — the false statement — is (D).
2. A. This one is a classic SAT problem. The key is knowing that one complete rotation equals the circumference of the wheel. Because circumference = 2 × π × radius, you have C = 2(3.14)(1.5) = 9.42 feet. Dividing 95 by 9.42 gives you 10.08, so your answer is 10. Give it up for (A).
3. D. Because ![]() and
and ![]() are tangents, the angles at A and C must be right angles. (If this fact is a surprise, turn back to Chapter 16. I can almost guarantee that this concept will show up in some form on the test.) Triangles OPC and OPA are right triangles, so the Pythagorean Theorem comes into play (and hits the ball out of the park). Because OA = 8, OB and OC are also 8 because all radii are equal. That makes OP = 8 + 9 = 17. OP is the hypotenuse, OC is a leg, and CP is a leg. So (CP)2 + (8)2 = (17)2; (CP)2 + 64 = 289; (CP)2 = 225; and CP = 15. Choice (D) is correct.
are tangents, the angles at A and C must be right angles. (If this fact is a surprise, turn back to Chapter 16. I can almost guarantee that this concept will show up in some form on the test.) Triangles OPC and OPA are right triangles, so the Pythagorean Theorem comes into play (and hits the ball out of the park). Because OA = 8, OB and OC are also 8 because all radii are equal. That makes OP = 8 + 9 = 17. OP is the hypotenuse, OC is a leg, and CP is a leg. So (CP)2 + (8)2 = (17)2; (CP)2 + 64 = 289; (CP)2 = 225; and CP = 15. Choice (D) is correct.
Circling in on a better vocabulary
Lots of vocabulary words — the kind you may find in reading comprehension passages or even in normal conversation — pop out of math lessons and land in the real world. For example, the line that touches a circle but doesn’t pierce it (a tangent) gives rise to the expression going off on a tangent (moving away from the main topic to something that is only marginally related at best), as in “Coop went off on a tangent about eggs when he was supposed to be discussing feather boas.” A related word, tangential, shows up in sentences such as “The dry cleaners’ association and the United Featherworkers of America criticized Coop’s tangential remarks.”
You probably know how to find the circumference of a circle (the distance around the edge). Well, the following words are all in the same family:
![]() Circumlocution: To talk around by speaking indirectly and avoiding a clear statement, as in “Answering controversial questions in an election year, politicians favor circumlocutions.”
Circumlocution: To talk around by speaking indirectly and avoiding a clear statement, as in “Answering controversial questions in an election year, politicians favor circumlocutions.”
![]() Circumnavigate: To sail around, as in “Bob circumnavigated the globe in a leaky washtub.”
Circumnavigate: To sail around, as in “Bob circumnavigated the globe in a leaky washtub.”
![]() Circumscribe: To limit; picture a warden drawing a circle around someone and forbidding him or her to cross the line.
Circumscribe: To limit; picture a warden drawing a circle around someone and forbidding him or her to cross the line.
![]() Circumspect: Cautious; think of an imaginary circle around yourself that you venture beyond only with extreme care.
Circumspect: Cautious; think of an imaginary circle around yourself that you venture beyond only with extreme care.
![]() Circumvent: To go around, as in “Bruckner circumvented the door alarm by breaking through the wall.”
Circumvent: To go around, as in “Bruckner circumvented the door alarm by breaking through the wall.”
A distant cousin of the circum family is circuitous, an adjective that may describe the sort of route taxi drivers take with tourists in the back seat (round and round, just to drive up the fare).
4. B. This one is a shaded-area problem, so your answer must be the circle’s area minus the square’s area. The square’s area is pretty simple to figure out: It’s (10)2 = 100. To find the circle’s area, you need to know its radius. You can make a diameter by drawing the diagonal of the square, like so:
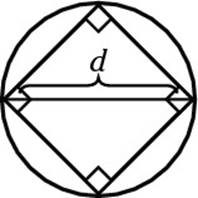
Look familiar? The diagonal of a square creates a 45-45-90 triangle, so the length of the diagonal is ![]() . (The SAT makers love special triangles.) The radius is half of the diameter,
. (The SAT makers love special triangles.) The radius is half of the diameter, ![]() , or
, or ![]() . Bingo. The area of the circle is
. Bingo. The area of the circle is ![]() . So your answer is 50π – 100, Choice (B).
. So your answer is 50π – 100, Choice (B).
5. D. The area of a parallelogram uses the same formula as a rectangle: base × height. Because the base, AE, is 9, and the area is 36, the height, AB, must be 4. (Don’t be fooled into thinking that AC is the height. The height is always perpendicular to the base, never slanted.) Meanwhile, BC = 12 – 9 = 3. This is yet another right triangle, so you can use the Pythagorean Theorem to get AC = 5. Even better, if you remember the 3-4-5 right triangle, you just know that the answer is 5 without having to do all the work. Choice (D) is your final answer.
6. C. The volume of a 3-D figure equals the area of its base times its height. Because the base is a circle, its area is πr2 = π(2)2 = 4π, or about 12.56 m2. Multiplying by 3, the height, gives you a volume of 37.68 m3. Dividing 37.68 m3 by 10 m3 per hour gives you 3.768 hours to fill the tank. This answer is a little bit closer to four hours than to 3.5 hours (3.75 would be exactly halfway), so you can round up to 4 hours. Four hours after 11 a.m. is 3 p.m. Choice (C) is correct.