Cracking the SAT
Part III
How to Crack the Math Section
Chapter 14
Geometry
While high school geometry can be amazingly complex and involve numerous proofs and theorems, SAT geometry is limited to testing a few basic rules. In fact, many of the rules the SAT tests are ones you learned in middle school. The SAT even provides you with most of the formulas you need at the beginning of each Math section. In this chapter you will learn how to apply these rules and formulas to the questions in the test. You will also learn that harder questions don’t test harder geometry; rather these questions simply are tricker or involve more steps.
SAT GEOMETRY: CRACKING THE SYSTEM
About a third of the math problems on the SAT will involve geometry. Fortunately, you won’t have to prove theorems or memorize tons of terms and formulas. That’s right, most of the geometric formulas you’ll need are on the first page of each Math section on the test, in the box entitled, “Reference Information.”
ETS Tries to Be Helpful
Not only do you not need any advanced geometric knowledge, but ETS helps you by giving you some basic geometric formulas in the front of each Math section.
Why would ETS give you all these geometric formulas? Because the SAT is not a geometry test like the ones you might see in school. ETS doesn’t care about proofs because it doesn’t want to spend the time and money to grade proofs. You need to know some rules of geometry, but not the way you do in a real geometry class.
Don’t be afraid to look back to grab a formula that you need!
The Princeton Review Way
The key to cracking SAT geometry is to gather all the available information in the problem. The best way to do that is to follow these simple steps:
1. Know the rules! The SAT doesn’t require any advanced geometric knowledge, but you will have to know the basics backward and forward.
2. Fill in the missing info. SAT geometry problems almost always leave out important information. Fill it in! Don’t forget to draw any missing pictures.
3. Write down any formulas required. All the area and volume formulas that you need will be provided. Write ’em down and fill in the values that you know.
4. Solve for any missing info. After you fill in the formula, solve.
Some problems won’t require you to work through all the steps. For easier geometry problems, you might need only steps 1 and 2. For harder problems, you may need all four steps. Either way, get in the habit of looking for missing information and filling it into the diagram.
Let’s get started with step 1: learning the basic rules.
BASIC PRINCIPLES: FUNDAMENTALS OF SAT GEOMETRY
The SAT doesn’t test any really difficult geometry, but you will need a thorough knowledge of several fundamental rules. You will use these fundamentals in applying the techniques that we will teach you later in the chapter. You don’t need to linger over these rules if you have already mastered them. But be sure you understand them completely before you move on. Some of these rules will be provided in the instructions on your SAT, but you should know them before you go to the test center. Consulting the instructions as you work is a waste of time. (On the other hand, if the Pythagorean theorem suddenly vaporizes from your brain while you are taking the test, don’t hesitate to peek back at the instructions.)
We divide SAT geometry into five basic topics:
· Degrees and angles
· Triangles
· Circles
· Rectangles and squares
· Odds and ends
Degrees and Angles
1. A circle contains 360 degrees.
Every circle contains 360 degrees. Each degree is ![]() of the total distance around the outside of the circle. It doesn’t matter whether the circle is large or small; it still has exactly 360 degrees.
of the total distance around the outside of the circle. It doesn’t matter whether the circle is large or small; it still has exactly 360 degrees.
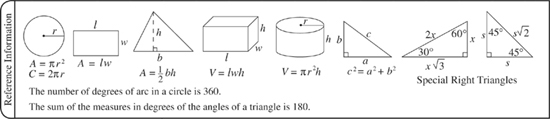
2. When you think about angles, remember circles.
An angle is formed when two line segments extend from a common point. If you think of the point as the center of a circle, the measure of the angle is the number of degrees enclosed by the lines when they pass through the edge of the circle. Once again, the size of the circle doesn’t matter; neither does the length of the lines.
Please refer to the figure on the next page for clarification.
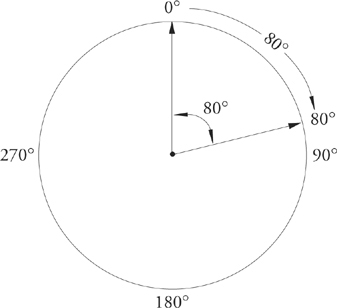
3. A line is a 180-degree angle.
You probably don’t think of a line as an angle, but it is one.
Think of it as a flat angle. The following drawings should help:
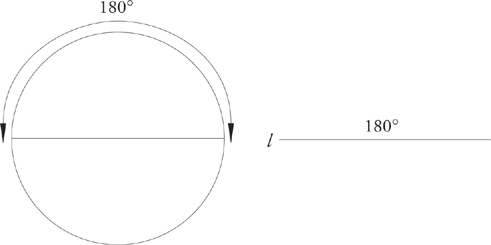
4. When two lines intersect, four angles are formed.
The following diagram should make this clear. The four angles are indicated by letters.
5. When two lines intersect, the angles opposite each other will have the same measures.
Such angles are called vertical angles. In the following diagram, angles a and c are equal; so are angles b and d.
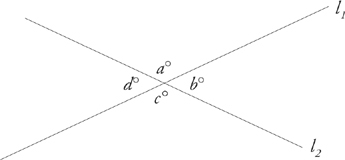
a + b + c + d = 360°
a = c, b = d
The measures of these four angles add up to 360 degrees. (Remember the circle.)
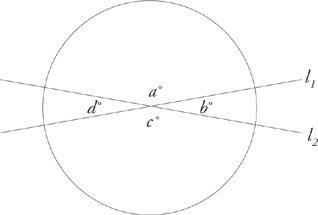
a + b + c + d = 360°
It doesn’t matter how many lines you intersect through a single point. The total measure of all the angles formed will still be 360 degrees.
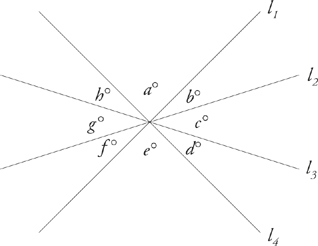
a + b + c + d + e + f + g + h = 360°
a = e, b = f , c = g, d = h
6. If two lines are perpendicular to each other, each of the four angles formed is 90 degrees. A 90-degree angle is called a right angle.
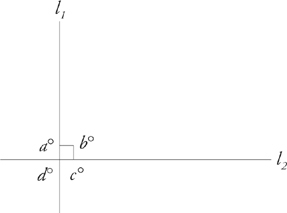
Angles a, b, c, and d all equal 90 degrees.
The little box at the intersection of the two lines is the symbol for a right angle. If the lines are not perpendicular to each other, then none of the angles will be right angles. Don’t assume that an angle is a right angle unless you are specifically told that it is right angle, either in the problem or with the 90° symbol.
7. When two parallel lines are cut by a third line, all of the small angles are equal, all of the big angles are equal, and the sum of any big angle and any small angle is 180 degrees.
Parallel lines are two lines that never intersect, and the rules about parallel lines are usually taught in school with lots of big words. But we like to avoid big words whenever possible. Simply put, when a line cuts through two parallel lines, two kinds of angles are created: big angles and small angles. You can tell which angles are big and which are small just by looking at them. All the big angles look equal, and they are. The same is true of the small angles. Lastly, any big angle plus any small angle always equals 180 degrees. (ETS likes rules about angles that add up to 180 or 360 degrees.)
In any geometry problem, never assume that two lines are parallel unless the question or diagram specifically tells you so. In the following diagram, angle a is a big angle, and it has the same measure as angles c, e, and g, which are also big angles. Angle b is a small angle, and it has the same measure as angles d, f, and h, which are also small angles.
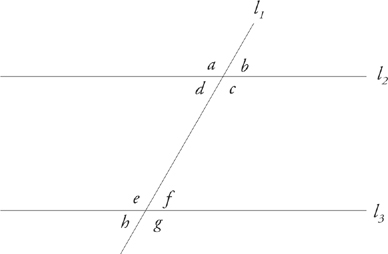
a = c = e = g
b = d = f = h
You should be able to see that the degree measures of angles a, b, c, and d add up to 360 degrees. So do those of angles e, f, g, and h. If you have trouble seeing it, draw a circle around the angles. What is the degree measure of a circle? Also, the sum of any small angle (such as d) and any big angle (such as g) is 180°.
Triangles
1. Every triangle contains 180 degrees.
The word triangle means “three angles,” and every triangle contains three interior angles. The measure of these three angles always adds up to exactly 180 degrees. You don’t need to know why this is true or how to prove it. You just need to know it. And we mean know it.
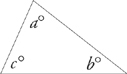
a + b + c = 180°
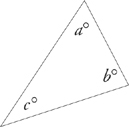
a + b + c = 180°
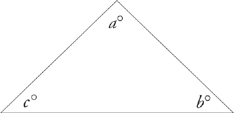
a + b + c = 180°
2. An isosceles triangle is one in which two of the sides are equal in length.
The angles opposite those equal sides are also equal because, as we just mentioned, angles opposite equal sides are also equal.
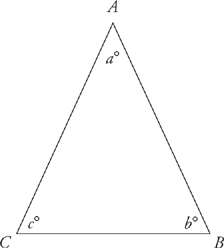
AB = AC AB ≠ BC
c = b c ≠ a
3. An equilateral triangle is one in which all three sides are equal in length.
Because the angles opposite equal sides are also equal, all three angles in an equilateral triangle are equal too. (Their measures are always 60 degrees each.)
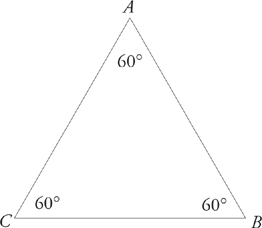
AB = BC = AC
4. A right triangle is a triangle in which one of the angles is a right angle (90 degrees).
The longest side of a right triangle, which is always opposite the 90-degree angle, is called the hypotenuse.
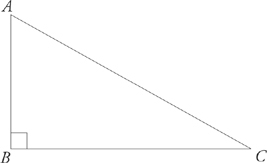
AC is the hypotenuse.
Some right triangles are also isosceles. The angles in an isosceles right triangle always measure 45°, 45°, and 90°.
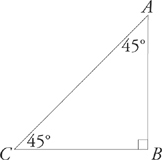
AB = BC
5. The perimeter of a triangle is the sum of the lengths of its sides.
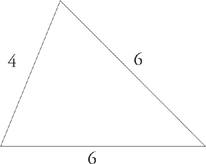
perimeter = 4 + 6 + 6 = 16
6. The area of a triangle is ![]() (base × height).
(base × height).
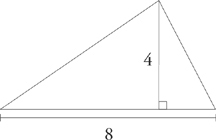
area = ![]() (8 × 4) = 16
(8 × 4) = 16
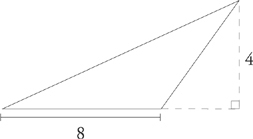
area = ![]() (8 × 4) = 16
(8 × 4) = 16
The Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. As we told you earlier, the hypotenuse is the longest side of a right triangle; it’s the side opposite the right angle. The square of the hypotenuse is its length squared. Applying the Pythagorean theorem to the following drawing, we find that c2 = a2 + b2.
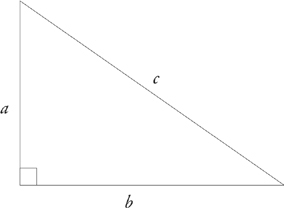
If you forget the Pythagorean theorem, you can always look it up in the box at the beginning of the Math section.
Special Right Triangles
There are many questions for which you won’t need the Pythagorean theorem. ETS writes very predictable geometry questions involving right triangles, and re-uses certain relationships. In these questions the triangles being used have particular ratios. There are two different types of special right triangles. The first involves the ratio of sides and the second involves the ratio of angles.
The most common special right triangles with side ratios are known as Pythagorean triplets. Here are ETS’s favorites:
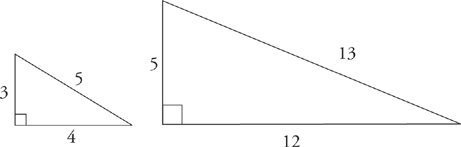
If you memorize these two sets of Pythagorean triplets (3-4-5 and 5-12-13), you’ll often be able to find ETS’s answer without using the Pythagorean theorem. If ETS gives you a triangle with a side of 3 and a hypotenuse of 5, you know right away that the other side has to be 4. Likewise, if you see a right triangle with sides of 5 and 12, you know the hypotenuse must be 13.
ETS also likes to use right triangles with sides that are simply multiples of the common Pythagorean triplets. For example, you might see a 6-8-10 or a 10-24-26 triangle. These sides are simply the sides of the 3-4-5 and 5-12-13 triangles multiplied by 2.
There are two types of special right triangles that have a specific ratio of angles. They are the 30°-60°-90° triangle and the 45°-45°-90° triangle. The sides of these triangles always have the same fixed ratio to each other. The ratios are as follows:
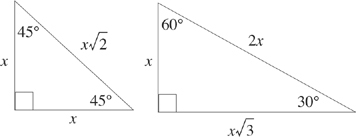
Let’s talk about a 45°-45°-90° triangle first. Did you notice that this is also an isosceles right triangle? The sides will always be the same. And the hypotenuse will always be the side times ![]() . Its ratio of side to side to hypotenuse is always 1 : 1 :
. Its ratio of side to side to hypotenuse is always 1 : 1 : ![]() . For example, if you have a 45°-45°-90° triangle with a side of 3, then the second side will also be 3 and the hypotenuse will be 3
. For example, if you have a 45°-45°-90° triangle with a side of 3, then the second side will also be 3 and the hypotenuse will be 3![]() .
.
Now let’s talk about a 30°-60°-90° triangle. The ratio of shorter side to longer side to hypotenuse is always 1 : ![]() : 2. For example, if the shorter side of a 30°-60°-90° triangle is 5, then the longer side would be 5
: 2. For example, if the shorter side of a 30°-60°-90° triangle is 5, then the longer side would be 5![]() and the hypotenuse would be 10.
and the hypotenuse would be 10.
The best news? Special right triangles and their ratios are also included in your reference information box on the test!
Angle-Side Relationships in Triangles
The longest side of any triangle is opposite the largest interior angle; the shortest side is opposite the smallest angle. In the following triangle, side a is longer than side b, which is longer than side c, because 80 > 60 > 40.
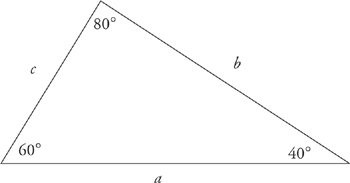
The same rule applies to isosceles and equilateral triangles. An isosceles triangle, remember, is one in which two of the sides are equal in length; therefore, the angles opposite those sides are also equal. In an equilateral triangle, all three sides are equal; so are all three angles.
Symbols
ETS doesn’t always write things out. Here’s a list of symbols ETS might use, along with a translation of each one into English:
|
Symbol |
Meaning |
|
∆ABC |
triangle ABC |
|
|
line segment AB |
|
AB |
the length of line segment AB |
Learn these symbols and keep an eye out for them!
Similar Triangles
Similar triangles have the same shape, but they are not necessarily the same size. Having the same shape means that the angles of the triangles are identical. Look at the following two similar triangles:
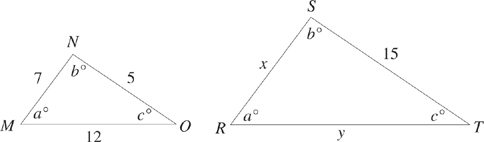
These two triangles both have the same set of angles, but they aren’t the same size. Whenever this is true, the sides of one triangle are proportional to those of the other. Notice that sides NO and ST are both opposite the angle that is a°. These are called corresponding sides, because they correspond to the same angle. So the lengths of ![]() and
and ![]() are proportional to each other. In order to figure out the lengths of the other sides we set up a proportion:
are proportional to each other. In order to figure out the lengths of the other sides we set up a proportion: ![]() . Now fill in the information that you know:
. Now fill in the information that you know: ![]() . Cross-multiply and you find that x = 21. You could also figure out the length of y:
. Cross-multiply and you find that x = 21. You could also figure out the length of y: ![]() . So,
. So, ![]() , and y = 36. Whenever you have to deal with sides of similar triangles, just set up a proportion.
, and y = 36. Whenever you have to deal with sides of similar triangles, just set up a proportion.
Circles
1. The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter.
You’ll be given this information in your test booklet, so don’t stress over memorizing these formulas. You will always be able to refer to your test booklet if you forget them. Just keep in mind that the diameter is always twice the length of the radius (and that the radius is half the diameter).
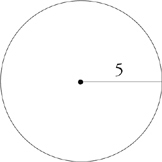
circumference = 2 × π × 5 = 10π
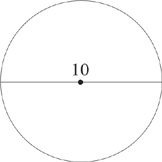
circumference = 10π
In math class you probably learned that π = 3.14 (or even 3.14159). On the SAT, π = 3+ (a little more than 3) is a good enough approximation. Even with a calculator, using π = 3 will give you all the information you need to solve difficult SAT multiple-choice geometry questions.
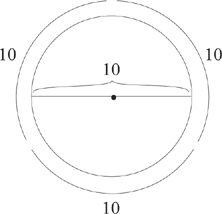
circumference = about 30
2. The area of a circle is πr2, where r is the radius of the circle.
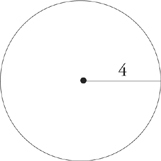
area = π42 = 16π
3. A tangent is a line that touches a circle at exactly one point. Any radius drawn from that tangent point forms a 90-degree angle.
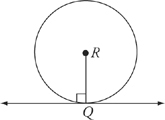
Rectangles and Squares
1. The perimeter of a rectangle is the sum of the lengths of its sides.
Just add them up.
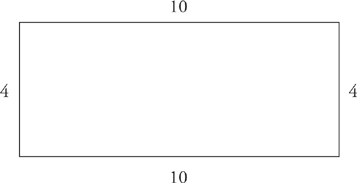
perimeter = 10 + 4 + 10 + 4 = 28
2. The area of a rectangle is length × width.
The area of the preceding rectangle, therefore, is 10 × 4, or 40.
3. A square is a rectangle whose four sides are all equal in length.
The perimeter of a square, therefore, is four times the length of any side. The area is the length of any side squared.
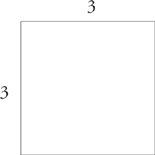
perimeter = 4 (3) = 12
area = 32 = 9
4. In rectangles and squares all angles are 90-degree angles.
It can’t be a square or a rectangle unless all angles are 90 degrees.
Polygons
Polygons are two-dimensional figures with three or more straight sides. Triangles and rectangles are both polygons. So are figures with five, six, seven, eight, or any greater number of sides. The most important fact to know about polygons is that any one of them can be divided into triangles. This means that you can always determine the sum of the measures of the interior angles of any polygon.
For example, the sum of the interior angles of any four-sided polygon (called a quadrilateral) is 360 degrees. Why? Because any quadrilateral can be divided into two triangles, and a triangle contains 180 degrees. Look at the following example:
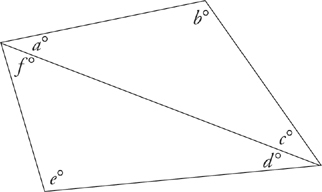
In the polygon on the previous page, a + b + c = 180 degrees; so does d + e + f. That means that the sum of the interior angles of the quadrilateral must be 360 degrees (a + b + c + d + e + f).
A parallelogram is a quadrilateral whose opposite sides are parallel. In the following parallelogram, side AB is parallel to side DC, and AD is parallel to BC. Because a parallelogram is made of two sets of parallel lines that intersect each other, we know that the two big angles are equal, the two small angles are equal, and a big angle plus a small angle equals 180 degrees. In the figure below, big angles A and C are equal, and small angles B and D are equal. Also, because A is a big angle and D is a small angle, A + D = 180 degrees.

Volume
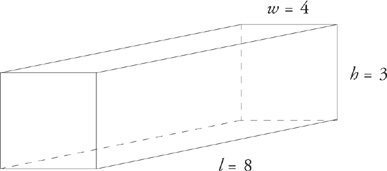
ETS will occasionally ask a question that will require you to calculate the volume of a rectangular solid (a box or a cube). The formula for the volume of a rectangular solid is length × width × height.
Volume = 8 × 4 × 3 = 96
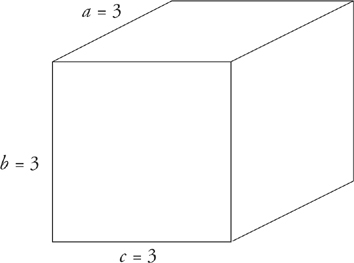
Because length, width, and height are equal in a cube, the volume of a cube can be calculated simply by cubing (where do you think they get the name?) the length of any edge of the cube.
Volume = 33 = 27
The Coordinate Plane
A coordinate plane is made up of two number lines that intersect at a right angle. The horizontal number line is called the x-axis, and the vertical number line is the y-axis.
The four areas formed by the intersection of the axes are called quadrants. The location of any point can be described with a pair of numbers (x, y), just the way you would point on a map: (0, 0) are the coordinates of the intersection of the two axes (also called the origin); (1, 2) are the coordinates of the point one space to the right and two spaces up; (–1, 5) are the coordinates of the point one space to the left and five spaces up; (–4, –2) are the coordinates of the point four spaces to the left and two spaces down. All these points are located on the diagram below.

Some of the questions on the SAT may require you to know certain properties of lines on the coordinate plane. Let’s talk about them.
Slope
You always read a graph from left to right. As you read the graph how much the line goes up or down is known as the slope. Slope is the rate of change of a line and is commonly known as “rise over run.” It’s denoted by the letter m. Essentially, it’s the change in the y-coordinates over the change in x-coordinates and can be found with the following formula:
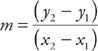
This formula uses the coordinates (x1, y1) and (x2, y2).
Let’s do an example. If you have the points (2, 3) and (7, 4), the slope of the line created by these points would be
![]()
So the slope of a line with points (2, 3) and (7, 4) would be ![]() , which means that every time you go up 1 unit, you travel to the right 5 units.
, which means that every time you go up 1 unit, you travel to the right 5 units.
Equation of a Line
The equation of a line can take multiple forms. The most common of these is known as the slope-intercept form. If you know the slope and the y-intercept, you can create the equation of a given line. A slope-intercept equation takes the form y = mx + b, where m is the slope and b is the y-intercept.
Let’s say that we know that a certain line has a slope of 5 (which is the same as ![]() ) and a y-intercept of 3. The equation of the line would be y = 5x + 3. You could graph this line simply by looking at this form of the equation. First, draw the y-intercept, (0, 3). Next, plug in a number for x and solve for y to get a coordinate pair of a point on the line. Now connect the point you just found with the y-intercept you already drew, and voilà, you have a line. If you want more points, you can create a table such as this one:
) and a y-intercept of 3. The equation of the line would be y = 5x + 3. You could graph this line simply by looking at this form of the equation. First, draw the y-intercept, (0, 3). Next, plug in a number for x and solve for y to get a coordinate pair of a point on the line. Now connect the point you just found with the y-intercept you already drew, and voilà, you have a line. If you want more points, you can create a table such as this one:
|
x |
y |
|
–2 |
–7 |
|
–1 |
–2 |
|
0 |
3 |
|
1 |
8 |
Take a look at the finished product:
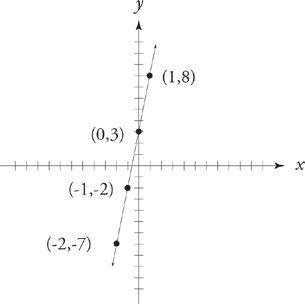
Things You Can Do to a Line
The midpoint formula gives the midpoint of ST, with points S (x1, y1) and T (x2, y2). It’s simply the average of the x-coordinates and the y-coordinates. In our example, the midpoint would be ![]() .
.
The distance formula looks quite complicated. The easiest way to solve the distance between two points is to connect them and form a triangle. Then use the Pythagorean theorem. Many times, the triangle formed is one of the common Pythagorean triplets (3-4-5 or 5-12-13).
Remember Functions?
Sometimes, instead of seeing the typical y = mx + b equation, or something similar, you’ll see f(x) = mx + b. Look familiar? Graphs are just another way to show information from a function. Functions show information algebraically and graphs show functions geometrically (as pictures).
Here’s an example. The function f(x) = 3x – 2 is shown graphically as the following:
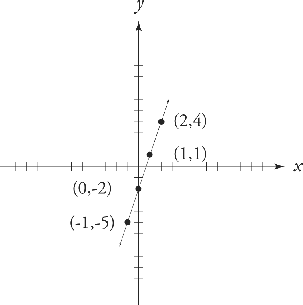
If you’re not comfortable with graphs, feel free to skip the oddball graphing question, but for most of you, these aren’t half as frustrating as some other topics (fractions, for example). The reason ETS asks function questions is to test whether you can figure out the relationship between a function and its graph. To tackle these questions, you need to know that the independent variable, the x, is on the x-axis, and the dependent variable, the f(x), is on the y-axis. For example, if you see a function of f(x) = 7, then you need to understand that this is a graph of a horizontal line wherey = 7.
Graphing Functions
One type of function question you might be asked is how the graph of a function would shift if you added a value to it. Again, there are not going to be a lot of these questions, so feel free to skip the few that appear if you don’t feel comfortable answering them.
Here is a quick guide (c is a constant) for the graph of f(x) = x2:
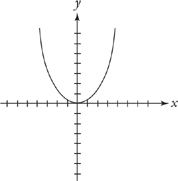
For f(x) + c, the graph will shift up c units, as shown in the diagram below:
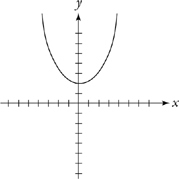
Conversely, f(x) – c will shift the graph down by c units:
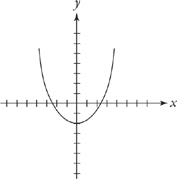
For f(x + c), the graph will shift c units to the left:
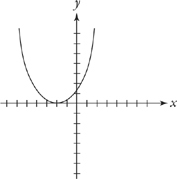
For f(x – c), the graph will shift to the right by c units:
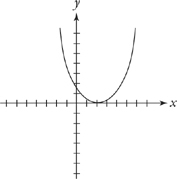
You may have realized how easy these problems would become if you simply put them into your graphing calculator. If you’ve got one, type in the function; if not, remember the four simple rules for transforming graphs.
BASIC PRINCIPLES: PRACTICE
Okay, now that you’ve mastered the rules, you’re ready to knock out some problems.
Warm up with this one:
![]()
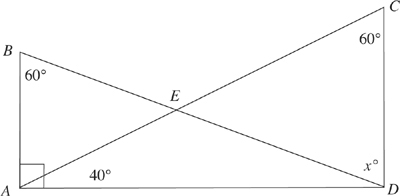
6. What is the value of x in the figure above?
(A) 20
(B) 30
(C) 40
(D) 50
(E) 60
Here’s How to Crack It
Look at the way ETS presents the problem. We have two triangles, but only two angles are given in each figure. Let’s start filling in the missing information. Triangle ABD has a 90-degree angle and a 60-degree angle. What’s missing? Write 30 degrees in for the third angle, angle EDA. Now let’s move to triangle ACD. This figure has angle measurements of 60 and 40. Fill in the missing third angle of 80. Now we have enough information to solve the problem. Angle D is 80 degrees and part of it is 30, so the leftover part, x, must be 50. D is the correct answer.
![]()
Here’s another one:
![]()
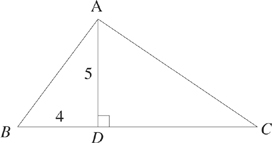
8. If the area of ∆ABC in the figure above is 30, what is the length of DC ?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 12
Here’s How to Crack It
In this problem, there’s not much missing information to fill in. Perhaps you filled in the missing 90-degree angle in triangle ABD. If so, good job. Even though it’s not important for this problem, it’s good to get into the habit of filling in information. The problem also gives us the area of the triangle. Write out the area formula. (You do remember the formula, right? If not, flip back to this page.) Fill in what you know. The area is 30, and the height is 5. All we have to do is solve for the base, which is 12. If BC is 12 and BD is 4, then DC must be 8. D is the answer.
![]()
Now you’re warmed up. Let’s try a more challenging problem:
![]()
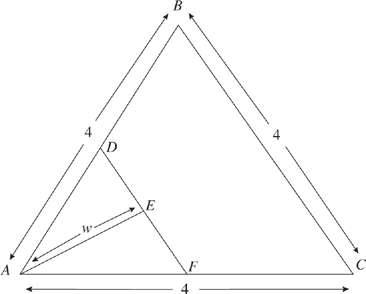
15. Triangle ABC is equilateral and angle AEF is a right angle. D is the midpoint of AB, F is the midpoint of AC, and E is the midpoint of DF. What is the value of w ?
(A) 1
(B) ![]()
(C) 2
(D) 2![]()
(E) 2![]()
Here’s How to Crack It
This problem has a lot more going on in it. But if we take it piece by piece, we’ll crack it. Let’s start filling in some information. The first thing the problem tells us is that triangle ABC is equilateral. Mark 60 degree angles on the figure. Next, we see that angle AEF is a right angle. Write that in as well. The problem also conveniently tells us that D and F are the midpoints of AB and AC, respectively. Therefore, AD and AF are 2. Finally, the last piece of information reveals that E is the midpoint of DF; mark DE and EF as equal.
Now, what do we have? Triangle AEF is a right triangle, with a hypotenuse of 2 and a leg of 1. Hmm, perhaps the good ol’ Pythagorean theorem can help us. Plug the numbers into the theorem, and you’ll see that the answer is B.
You may have also noticed that triangle ADE is a 30°-60°-90° triangle with hypotenuse 2, which means that DE is 1 and w, opposite the 60°, is the square root of 3. In geometry questions on the SAT, there will often be multiple ways to get to the answer. On the day of the test, use whichever way you are most comfortable with.
![]()
BALLPARKING
You may be thinking, “Wait a second, isn’t there an easier way?” By now, you should know that of course there is, and we’re going to show you. On many SAT geometry problems, you won’t have to calculate an exact answer. Instead, you can estimate an answer choice. We call thisBallparking.
Ballparking is extremely useful on SAT geometry problems. At the very least, it will help you avoid careless mistakes by immediately eliminating answers that could not possibly be correct. In many problems, Ballparking will allow you to find ETS’s answer without even working out the problem at all.
For example, on many SAT geometry problems, you will be presented with a drawing in which some information is given and you will be asked to find some of the information that is missing. In most such problems, ETS expects you to apply some formula or perform some calculation, often an algebraic one. But you’ll almost always be better off if you look at the drawing and make a rough estimate of ETS’s answer (based on the given information) before you try to work it out.
The basic principles you just learned (such as the number of degrees in a triangle and the fact that π ≈ 3) will be enormously helpful to you in Ballparking on the SAT. You should also know the approximate values of several common square roots. Be sure to memorize them before moving on. Knowing them cold will help you solve problems and save time, even if your calculator has a square root function.
Square Roots
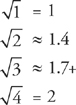
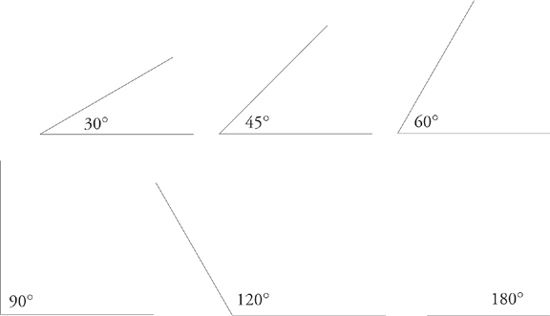
You will also find it very helpful if you have a good sense of how large certain common angles are. Study the following examples.
How High Is the Ceiling?
If your friend stood next to a wall in your living room and asked you how high the ceiling was, what would you do? Would you get out your trigonometry textbook and try to triangulate using the shadow cast by your pal? Of course not. You’d look at your friend and think something like this: “Dave’s about 6 feet tall. The ceiling’s a couple of feet higher than he is. It must be about 8 feet high.”
Your ballpark answer wouldn’t be exact, but it would be close. If someone later claimed that the ceiling in the living room was 15 feet high, you’d be able to tell her with confidence that she was mistaken.
You’ll be able to do the same thing on the SAT. Every geometry figure on your test will be drawn exactly to scale unless there is a note in that problem telling you otherwise. That means you can trust the proportions in the drawing. If line segment A has a length of 2 and line segment B is exactly half as long, then the length of line segment B is 1. All such problems are ideal for Ballparking.
When You Can’t Measure, Sketch, or Ballpark
You will sometimes encounter geometry problems that have no diagrams, diagrams not drawn to scale, or diagrams containing only partial information. In these cases, you should use the given information to sketch your own complete diagram and then use your drawing as a basis for Ballparking. Don’t hesitate to fill your test booklet with sketches and scratch work: This is precisely what you are supposed to do. Finding ETS’s answer will be much harder, or even impossible, if you don’t take full advantage of the information ETS gives you.
Here’s an example:
![]()
16. All faces of a cube with a 4-meter edge are covered with striped paper. If the cube is then cut into cubes with 1-meter edges, how many of the 1-meter cubes have striped paper on exactly one face?
(A) 24
(B) 36
(C) 48
(D) 60
(E) 72
Here’s How to Crack It
This problem doesn’t have a diagram. It would be much easier to solve if it did. What should you do? Draw a diagram, of course! Just sketch the cube quickly in your test booklet and mark it off into 1-meter cubes as described. Your sketch might look like this:
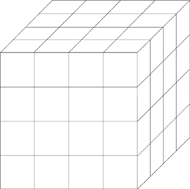
You should be able to see that there are four cubes on each side of the big cube that will have striped paper on only one face (the four center cubes—all the other cubes have at least two exterior sides). Because a cube has six sides, this means that ETS’s answer is choice A.
![]()
PLUGGING IN
As you learned in Chapter 13, Plugging In is a powerful technique for solving SAT algebra problems. It is also very useful on geometry problems. On some problems, you will be able to plug in ballpark values for missing information and then use the results either to find ETS’s answer directly or to eliminate answers that could not possibly be correct.
Here’s an example:
![]()
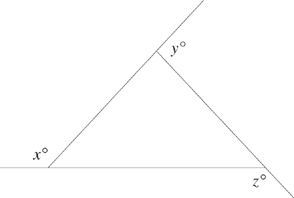
16. In the figure above, what is the value of x + y + z ?
(A) 90
(B) 180
(C) 270
(D) 360
(E) 450
Here’s How to Crack It
We don’t know the measures of the interior angles of the triangle in the drawing, but we do know that the three interior angles of any triangle add up to 180, and 180 divided by 3 is 60. Now, simply plug in 60 for the value of each interior angle.
This doesn’t give you ETS’s answer directly; the problem does not ask you for the sum of the interior angles. But Plugging In does enable you to find ETS’s answer. Look at the redrawn figure:
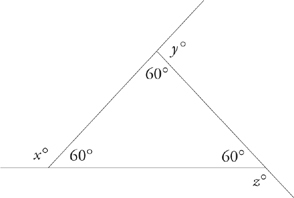
If the marked interior angle is 60, what must x be? Remember that every line is a 180-degree angle. That means that the measure of x must be 180 – 60, or 120. You can now do the same thing for the other two angles. Using this method you find that x, y, and z each equal 120. That means that x+ y + z = 360. ETS’s answer, therefore, is choice D.
![]()
Ballparking like this won’t always give you ETS’s exact answer, but it will usually enable you to eliminate at least three of the four incorrect choices. Other kinds of geometry problems also lend themselves to Plugging In.
Here’s another example:
![]()
20. The base of triangle T is 40 percent less than the length of rectangle R. The height of triangle T is 50% greater than the width of rectangle R. The area of triangle T is what percent of the area of rectangle R ?
(A) 10
(B) 45
(C) 90
(D) 110
(E) 125
Here’s How to Crack It
This is a really hard problem. You should recognize that A, C, and D are Joe Bloggs answers and should be eliminated. Even if you don’t see this, you’ll still be able to find the right answer by sketching and plugging in.
When plugging in, always use numbers that are easy to work with. Let’s say the length of the rectangle is 10; that means that the base of the triangle, which is 40 percent smaller, is 6. Now if we plug 4 in for the width of rectangle R, then the height of triangle T is 6. You should come up with two sketches that look like this:
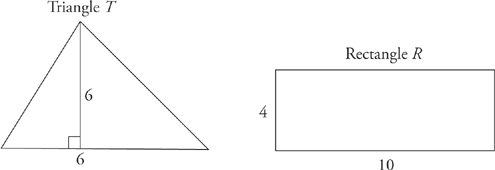
T has an area of ![]() bh, or 18. R has an area of 40. Now set up the translation: 18 =
bh, or 18. R has an area of 40. Now set up the translation: 18 = ![]() (40) where x represents what percent the triangle is of the rectangle. Solve for x and you get 45. The correct answer is B.
(40) where x represents what percent the triangle is of the rectangle. Solve for x and you get 45. The correct answer is B.
![]()
As you can see, advanced geometry problems actually don’t involve any advanced principles. Rather, these problems are harder simply because they combine multiple concepts (and therefore require a lot more work). However, if you follow The Princeton Review’s strategy—and know your basic rules—you should have a pretty good handle on these.
Let’s give another difficult one a shot:
![]()
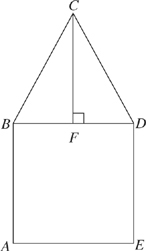
14. In the figure above, BCD is an equilateral triangle, F is the midpoint of BD, and CF = 3![]() . What is the length of the diagonal of square ABDE ?
. What is the length of the diagonal of square ABDE ?
(A) 3![]()
(B) 3![]()
(C) 6
(D) 6![]()
(E) 6![]()
Here’s How to Crack It
First, you should fill in the missing angles on triangle BCD. It looks like we have a 30°-60°-90° right triangle for FCD. This is one of ETS’s favorite triangles. In fact, the test writers love it so much that they provide all the information you need to know about it in the beginning of each Math section. Even so, it might be helpful to memorize the relationship of sides in the 30°-60°-90° triangle. If the smallest side, which is opposite the 30-degree angle, is x, then the hypotenuse will be 2x. The medium-length side opposite the 60-degree angle will be x![]() .
.
Conveniently, the side opposite the 60-degree angle is 3![]() . Therefore, x must be 3. And if side DF is 3, then so too must be side BF. You’ve now discovered that the side of the square is 6; you’re in the home stretch. Because you need the diagonal of the square, you can use the Pythagorean theorem. 62 + 62 = c2. Solving for the diagonal, you should get 6
. Therefore, x must be 3. And if side DF is 3, then so too must be side BF. You’ve now discovered that the side of the square is 6; you’re in the home stretch. Because you need the diagonal of the square, you can use the Pythagorean theorem. 62 + 62 = c2. Solving for the diagonal, you should get 6![]() , which is D.
, which is D.
You may have also noticed that the diagonal of square ABDE is a 45°-45°-90° triangle. Noticing that can save you the trouble of using the Pythagorean theorem.
![]()
Had enough? Maybe we should try one more.
![]()
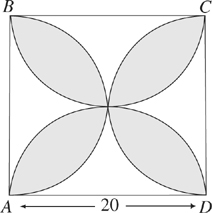
19. The shaded region in square ABCD above is composed of the intersections of circular regions. What is the area of the shaded region?
(A) 20π
(B) 40(π – 2)
(C) 200(π – 2)
(D) 100π
(E) 400π
Here’s How to Crack It
This problem is a nightmare. Notice the difficulty level—it’s right up there at the top. But even the most difficult problems can be cracked if you know how to approach them. Instead of doing all of the math, which would take ages, let’s engage in a little Ballparking. Start with what you know: You have a square with a side length of 20. The question asks for the area of the leaf-shaped portions. The entire area of the square is 400. Ballpark the amount of the picture taken up by the shaded region; it looks to be around half. So we need an answer around 200. Let’s go to the choices:
(A) 20π ≈ 60 Too small
(B) 40(π – 2) ≈ 40 Too small
(C) 200(π – 2) ≈ 200 Looks good!
(D) 100π ≈ 314 Too big
(E) 400π ≈ 1,200 Way too big!
The answer is C.
![]()
You may think that this isn’t the “right” way to do the problem, but that’s not the issue. The goal is to get as many points as possible, by any means possible. In most areas of your life, we wouldn’t recommend that sort of mindset, but for the SAT it’s okay.
Summary
· Degrees and angles:
· A circle contains 360 degrees.
· When you think about angles, remember circles.
· A line is a 180-degree angle.
· When two lines intersect, four angles are formed; the sum of their measures is 360 degrees.
· When two parallel lines are cut by a third line, the small angles are equal, the big angles are equal, and the sum of a big angle and a small angle is 180 degrees.
· Triangles:
· Every triangle contains 180 degrees.
· An isosceles triangle is one in which two of the sides are equal in length, and the two angles opposite the equal sides are equal in measure.
· An equilateral triangle is one in which all three sides are equal in length, and all three angles are equal in measure (60 degrees).
· A right triangle is one in which one of the angles is a right angle (90 degrees).
· The perimeter of a triangle is the sum of the lengths of its sides.
· The area of a triangle is ![]() bh.
bh.
· The height must form a right angle with the base.
· The Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. Remember ETS’s favorite Pythagorean triplets (3-4-5 and 5-12-13).
· Remember the other special right triangles: 45°-45°-90° and 30°-60°-90°.
· Similar triangles have the same angles and their lengths are in proportion.
· Circles:
· The circumference of a circle is 2πr or πd, where r is the radius of the circle and d is the diameter.
· The area of a circle is πr2, where r is the radius of the circle.
· A tangent touches a circle at one point; any radius that touches that tangent forms a 90-degree angle.
· Rectangles and squares:
· The perimeter of a rectangle is the sum of the lengths of its sides.
· The area of a rectangle is length × width.
· A square is a rectangle whose four sides are all equal in length.
· Any polygon can be divided into triangles.
· The volume of a rectangular solid is length × width × height. The formulas to compute the volume of other three-dimensional figures are supplied in the instructions at the front of every Math section of the SAT exam.
· You must know how to locate points on a grid.
· When you encounter a geometry problem on the SAT, Ballpark the answer before trying to work it out.
· You must be familiar with the size of certain common angles.
· Most SAT geometry diagrams are drawn to scale. Use your eyes before you use your pencil. Try to eliminate impossible answers.
· When a diagram is not drawn to scale, redraw it.
· When no diagram is provided, make your own; when a provided diagram is incomplete, complete it.
· When information is missing from a diagram, ballpark and plug in.
· Some extremely difficult SAT geometry problems can be solved quickly and easily through sketching and Ballparking, but you will have to stay on your toes. The way to do this is always to ask yourself three questions:
· What information have I been given?
· What information have I been asked to find?
· What is the relationship between these two pieces of information?