SAT Test Prep

CHAPTER 6
WHAT THE SAT MATH IS REALLY TESTING

Lesson 4: Simplifying Problems

Beeline, Substitute, Combine, and Cancel

When a problem seems overwhelming, try one of these four simplification strategies: beelining, substituting, combining, and canceling.

Look for the Beeline—The Direct Route

Many SAT problems have “beelines”—direct paths from the given information to the answer. We sometimes miss the “beeline” because we get trapped in a knee-jerk response—for instance, automatically solving every equation or using the Pythagorean theorem on every right triangle. Avoid the knee-jerk response. Instead, step back and look for the “beeline.”

If and , what is the value of ?

This problem looks tough because of all the unknowns. You might do the knee-jerk thing and try to solve for a, b, and c. Whoa, there! Step back. The question doesn”t ask for a, b, and c. It asks for a fraction that you can get much more directly. Notice that just multiplying the two given fractions gets you almost there: . This is close to what you want—all you have to do is divide by 3 to get Substituting the given values of the fractions gives you which is the value of

Simplify by Substituting

The simplest rule in algebra is also the most powerful: Anything can be substituted for its equal. When you notice a complicated expression on the SAT, just notice if it equals something simpler, and substitute!

If and , then what is the value of

Again, take a deep breath. Both the equation and the fraction look complicated, but you can simplify by 16 2 3 5 just remembering that anything can be substituted for its equal. Notice that appears in both the equation and the fraction. What does it equal? Subtract y from both sides of the equation to get . If you substitute for in the fraction, you get 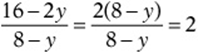. Nice!

Simplify by Combining or Canceling

Many algebraic expressions can be simplified by combining or canceling terms. Always keep your eye out for like terms that can be combined or canceled and for common factors in fractions that can be canceled.

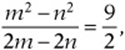If m and n are positive integers such that and what is the value of ?

To simplify this one, it helps to know a basic factoring formula from Chapter 8, Lesson 5: . If you factor the numerator and denominator of the fraction, a common factor reveals itself, and it can be canceled: 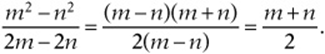Since must equal 9.

If and , then for how many values of x does ?

(A) 0

(B) 1

(C) 2

(D) 3

(E) 4

Remember the simple rule that anything can be substituted for its equal, and then cancel to simplify. Since , you can say that .

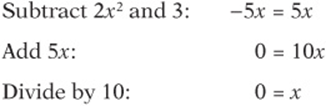
So the answer is (A) 0, right? Wrong! Remember that the question asks for how many values of x are the function values equal. Since we only got one solution for x, the answer is (B)1.

Concept Review 4: Simplifying Problems

Simplify the following expressions.

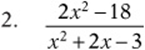
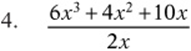
Solve the following problems with substitution.

6. If and , then what is the value of x?

7. If , what is the value of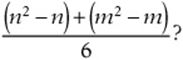

8. For all real numbers . What is the value of ?

SAT Practice 4: Simplifying Problems

1. If and , then

(A) 12

(B) 6

(C) 4

(D) 0

(E) –4

2. If , , and , then

(A) 4

(B) 2

(C) 1

(D) 0

(E) –1

3. If and , what is the value of ?

(D) 2

(E) 8

Questions 4 and 5 pertain to the following definition:

For all non-zero real numbers k, let

4. Which of the following is equivalent to ?

(C) ^1

(E) ^2

5. Other than 0, what is the only value of k for which ^^k is undefined?

Answer Key 4: Simplifying Problems

Concept Review 4

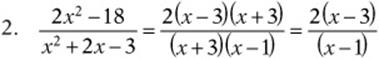
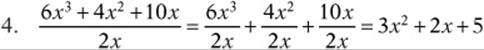
6. Substitute into to get

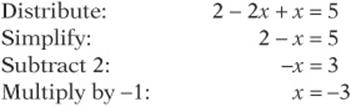
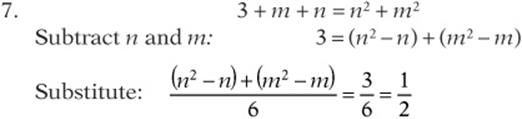
SAT Practice 4

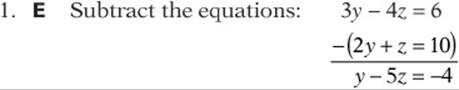
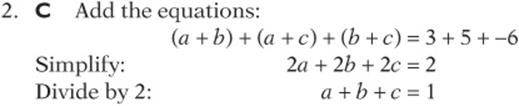
3. D Start by simplifying the expressions:

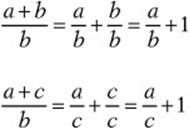
Substituting into the original equations gives

4. D Begin by simplifying by substitution: But be careful not to pick (A) ^1/6 because

Notice that the choices must be evaluated first before we can see which one equals 1/6. Notice that choice (D)

5. 1 Begin by simplifying ^^k by substitution:

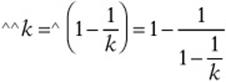
Yikes! That doesn”t look simple! But think about it: why is it that k can”t be 0? Because division by 0 is undefined, and k is in a denominator. But notice that is also in a denominator, so can”t be 0, either!

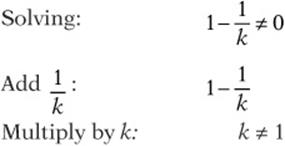
Then check by noticing that ^^1 is undefined:

, and 1/0 is undefined.